MATH 581: Mathematics of Data Science

Instructor Information

Instructor: Dmitriy Drusvyatskiy
Lecture: MW 1:00-2:20 PM
Office hours: F 12:00-1:00 PM and by appointment
Office: PDL C-434
Email: ddrusv at uw.edu

Meeting Times and Location

lecture time: Monday and Wednesday 1:00-2:20 PM
lecture location: Mary Gates Hall (MGH) 238

Course Description

Description: This is a three-term sequence covering the fundamentals of mathematics of data science. The basic question we will address is how does one “optimally” extract information from high dimensional data. The course will cover material from a few different fields, most notably high dimensional probability, statistical and machine learning, and optimization.

Textbook

We will use a number of different texts:

• Roman Vershynin, “High-dimensional probability: An introduction with applications in data science.”

• Martin J. Wainwright, “High-dimensional statistics: A non-asymptotic viewpoint.”

• Terence Tao, “Topics in random matrix theory.”

• Trevor Hastie, Robert Tibshirani, Jerome Friedman, “The Elements of statistical learning: data mining, inference, and prediction.”

• Francis Bach, “Learning theory from first principles.”

• Amir Beck, “First-order methods in optimization.”

• Sebastian Bubeck, “Convex Optimization: Algorithms and Complexity.”

• Shai Shalev-Shwartz, Shai Ben-David, “Understanding Machine Learning: From Theory to Algorithms.”

Requirements and Grading

• Biweakly problem sets with solutions written in LaTex (100% of the grade). Since, there is no TA for this course, the grading will be on the scale:

  • 0 (did not much work, if any),

  • 1 (did at least 50% of the homework),

  • 2 (did at least 80% of the homework).

Collaboration

You may work together on problem sets, but you must write up your own solutions. You must also cite any resources which helped you obtain your solutions.

Weakly Schedule

• Chapter 1: Concentration Inequalities

  • Introduction to the curse of dimensionality (Monte-Carlo simulation, Empirical Risk Minimization) (Lecture 1)

  • Review of basic probability and limit theorems (Lecture 2)

  • Chernoff Bound and SubGaussian random variables (Lecture 3)

  • Hoeffding and Chernoff inequalities; applications (robust mean estimation with median of means, approximate regularity of Erdos-Renyi graphs) (Lecture 4, Lecture 5)

  • Sub-Exponential Random Variables and Bernstein's Inequality; applications (dimensionality reduction with Johnson-Lindenstrauss lemma) (Lecture 6)

  • Fast Johnson-Lindenstrauss transformation (Lecture 7/8)

  • Functions of independent random variabels: McDiarmid inequality and Gaussian concentration (Lecture 9/10) (Nice reference to Talagrant and Gaussian concentration inequalities)

  • Concentration, moments, and Orlicz norms (Lecture 11)

• Chapter 2: Random Vectors in High Dimensions (Lecture 12/13)

  • Concentration of the norm

  • Isotropic Distributions

  • Similarity of Normal and Spherical Distributions

  • Sub-Gaussian and Sub-Exponential Random Vectors

• Chapter 3: Introduction to Statistical Inference (Lecture 14/15)

  • Mean square error and the Bias-Variance decomposition

  • Maximum Likelyhood Estimation and examples

• Chapter 4: Linear Regression (Lecture 16/17)

  • Ordinary least squares

  • Ridge regression

• Chapter 5: Uniform Laws and Introduction to Statistical Learning (Lecture 18-20)

  • Uniform law via Rademacher complexity

  • Glivenko-Cantelli Theorem

  • Upper bounds on Rademacher complexity

  • Sample complexity of binary classification with VC dimension

  • Learning linear classes

  • Stable learning rules generalize

  • Learning without uniform convergence with convex losses

• Chapter 6: Metric entropy and Matrix Concentration (Lecture 21-31)

  • Nets, Covering numbers, and the metric entropy

  • Eigenvalaues and Singular values of sub-Gaussian random matrices

  • Matrix concentration

  • Controlling the operator norm of a random matrix by row/column norms

  • Applications: community detection, (sparse) covariance estimation, matrix completion; See also the paper "Clustering mixtures with unknown covariances"

• Chapter 7: Learning with kernels (Lecture 31-35)

  • Motivation: the Kernel trick and dimension-free generalization

  • Introduction to Hilbert spaces

  • Representer Theorem

  • Positive definite kernels and the reproducing kernel Hilbert space (RKHS)

  • Moore-Aronszajn theorem and continuity of point evaluations

  • Translation-invariant kernels

  • Generalization properties

• Chapter 8: Optimization for learning (Lecture 36-45)

  • Two paradigms: empirical risk minimization vs stochastic approximation

  • Illustration: gradient descent for least squares

  • Convexity: an interlude

  • Gradient descent

  • Accelerated gradient descent

  • Projected subgradient method

  • Minimax lower bound for deterministic convex optimization

  • Stochastic gradient method and Polyak-Juditsky averaging

  • Stochastic variance reduced gradient (SVRG)

• Chapter 9: Suprema of sub-Gaussian processes (Notes)

  • Motivation

  • Examples of sub-Gaussian processes

  • Dudley's entropy integral and chaining

  • From metric entropy to Gaussian width

  • Sudakov-Fernique inequality

  • Gordon's theorem and the matrix deviation inequality

  • Johnson Lindenstrauss lemma for infinite sets

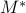  • -bound and escape through the mesh

• Chapter 11: Sparse recovery (Notes)

  • High dimensional signal recovery

  • signal recovery based on M* bound

  • exact recovery based on the escape theorem

  • deterministic conditions for recovery

  • recovery with noise (LASSO/BPDN)

• Chapter 10: Minimax lower bounds for estimation (Notes)

  • Minimax risk

  • Reduction to hypothesis testing

  • Le Cam's method based on binary testing

  • Interlude: Deviations between probability distributions

  • Applications: lower bounds for mean estimation and linear regression

• Chapter 12: Overparametrized models and the Polyak-Łojasiewicz (PL) inequality

  • Polyak's inequality and linear convergence of gradient descent (Notes)

  • Lojasiewicz inequality for analytic functions and finite length of gradient orbits

  • Kurdyka and desingularization of tame functions

  • Some extentions to nonsmooth functions

  • Introduction to neural networks

  • Transition to linearity and the PL condition for wide neural networks (Paper 1, Paper 2)

Homework Problems

• HW 1 (due Friday October 20th (slide it under my door)):

  • Reading: Vershynin (Chapter 2, Sections 3.1-3.4)

  • Optional Reading: Wainwright (Chapter 1, Chapter 2) and Vershynin (Sections 3.5-3.8)

  • Exercises: Vershynin (1.3.3, 2.2.10, 2.5.10, 2.5.11, 3.3.5, 3.4.4)

• HW 2 (due Friday November 10th (slide it under my door)):

  • Exercises: Vershynin (2.4.4, 2.5.7, 2.5.9, 2.6.5, 2.6.6, 3.3.3 )

• HW 3 (due Friday December 1st (slide it under my door)):

  • Reading: Wainwright (Chapter 4)

  • Exercises: (HW3)

• HW 4 (due Friday February 2nd (slide it under my door)):

  • Reading: Vershynin (Chapter 4)

  • Exercises: Vershynin (4.1.4, 4.4.6, 4.4.7, 4.5.2, 4.6.2, 4.7.6)

• HW 5 (due Friday February 23rd (slide it under my door)):

  • Reading: Vershynin (Chapter 5.4), Wainwright (Chapter 6)

  • Exercises: Vershynin (the version at this link Book) (5.4.5 (f)-(g), 5.4.11, 5.4.13, 5.4.15)

• HW 6 (due Friday April 3rd (slide it under my door)):

  • Exercises: 3.3, 3.5, 3.15, 5.12, 5.13, 5.14, 5.15 in the (text)