March 19, 2019
Here is a histogram of final exam scores:
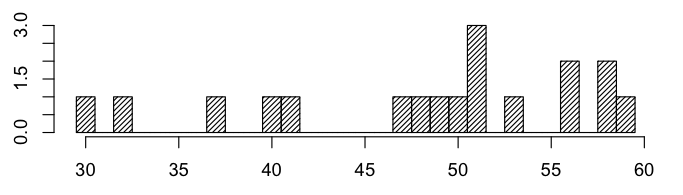
March 13, 2019
Here are some hints and comments on problems 9.7, 9.8, 9.9, 9.10, 9.13, and 9.14 .
- 9.7: To show f-1 is a bijection, you need to show that f-1 is one-to-one and onto. To show it is onto, start with an element of a. You need to find an element b of B such that f-1(b)=a. Since f itself is a function from A to B, you can use f to come up with this element b. To show f-1 is one-to-one, start by assuming f-1(b1) = f-1(b2). What happens if you apply f "to both sides" of the equation?
- 9.8: (a) Given an element in C, you need to "pull it back" to an element in
A. Do this in two steps: use properties of g to pull it back to B, and
then properties of f to pull it back to A.
(b) Try contradiction/contrapositive.
(c) Try drawing various situations, as in figure 9.1. Keep things simple.
(d) Contrapositive is pretty effective here. - 9.9: The main thing to do is to argue that there is a set C such that f:A->C is onto. Hint: We have a special name for this set C. Then argue that f:A->C is one-to-one, and you've got it.
- 9.10: This is an example of one of the kinds of functions you will eventually encounter in real analysis courses. This proof will involve a few cases. One part of your proof will involve the fact that we cannot have 2x=-3y with x rational and y irrational (why?).
- 9.13: This is getting back to a calculus-type real-valued function. Think a lot about the graphs of the two parts of the function. If you have a way to do so with software, plot the graphs and try various c values. If not, sketch a few cases by hand to get the idea. You will need the graphs of the two parts of the definition to "meet up" in a certain way in order for the function to be a bijection.
- 9.14: This problem is a chance to think about functions where the "left" and "right" sets are quite different things. Give yourself a bunch of examples to get the hang of it: what are f(2), f(1), f(0), f(-1) for example? Don't just plug these x into the definition: we are talking about subsets of the reals: what are these subsets "like"? Can you draw a picture of them? Look at examples until you have a good sense of how the function "works". Then think about answering the question.
March 12, 2019
I recommend working old final exams to practice for the upcoming final.
Since we were not able to cover Cardinality (chapter 10), problems related to that topic should be skipped as you study the old finals. Here is a list of problems to skip. Note that most problems on all finals are worth doing; this list shows just the ones not to do.
- Spring 2016 - #3
- Spring 2015 - all problems ok!
- Winter 2015 - all problems ok!
- Autumn 2014 - all problems ok!
- Winter 2014 - #1
- Spring 2013, B - #2 (b)
- Spring 2013, C - all problems ok!
- Winter 2013 - #4, 7
- Spring 2012, A - #1, 6
- Spring 2012, B - #1, 6
March 3, 2019
Here is a histogram of midterm 2 scores:
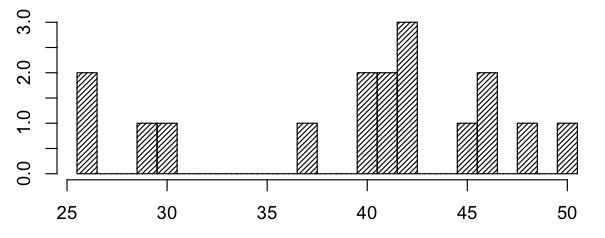
Median score was 41.
February 23, 2019
To study for the upcoming midterm, I recommend that you first read through all of the homework you have had returned. Check that you understand everything you did, and especially pay attention to any proofs that you did not receive full points for: make sure you understand how your proof was not completely correct and how to do write the proof correctly. The best thing to do is write out fresh correct proofs, particularly for any proofs that you lost points on, or that you find confusing or hard to create from scratch.
Then, try the problems below for extra practice.
- Spring 2016, MT2, problems 1, 3, 4
- Spring 2016, MT1, problems 2, 3
- Spring 2015, MT1, problems 1, 2, 4, 5
- Spring 2015, MT2, problems 1, 3, 4
- Winter 2015, MT2, problems 1, 2, 4, 5
- Autumn 2014, MT2, problems 2(a), 3, 5
February 6, 2019
Here is a histogram of the first midterm exam scores.
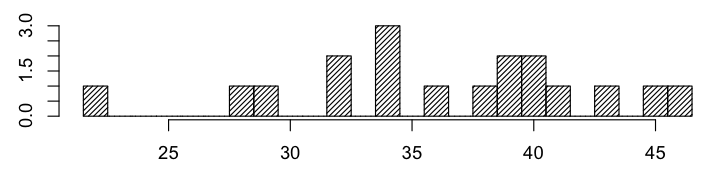
Here is a histogram of scores for homework 1.
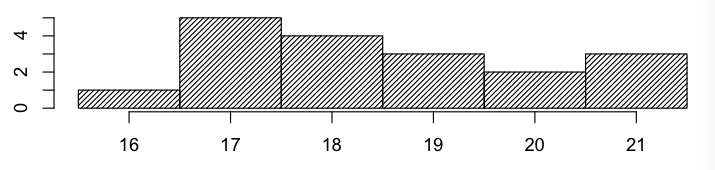
Here is a histogram of scores for homework 2.
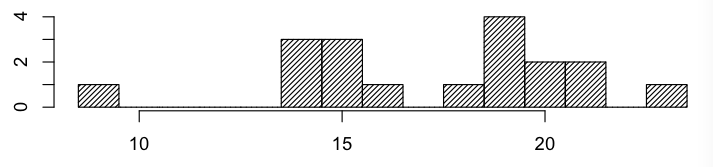
Here is a histogram of scores for homework 3.
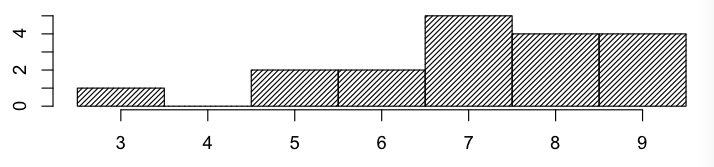
January 26, 2019
In preparation for the first midterm exam, here is what I recommend:
- Read chapters 1 through 4.
- Go through the assigned homework problems and make sure you understand how to do them. Pay particular attention to problems on graded homework that you did not get full points for.
- Here is a sample exam (answers) and an actual exam (answers Note: there is an error in the proof given in 3 (b). The proof should begin "Suppose c|a or c|b" and proceed from there.) from Dr. Taggart's 300 course (same topics and textbook as our course).
- Check out these problems from my exam archive (link at right):
- Spring 2016, exam #1, problems 1 and 4
- Spring 2015, exam #1, problem 3
- Winter 2015, exam #1, problem 5
- Autumn 2014, exam #1, problem 5
- Autumn 2014, final, problem 2
- Spring 2013, midterm, problem 2
- Spring 2013, B final, problem 6
- Spring 2013, C final, problem 6
- Winter 2013, midterm, problem 3
- Spring 2012, midterm, problem 4
January 22, 2019
Comments on Homework 2.
- Be careful with the use of the words "suppose" and "let".
They mean similar things, but there is an important difference. We use "let" when there
is no question that what we are specifying is possible.
For instance, we might write "Let x be an integer"; here, there is no question that there are integers, so we can let x be one of them.
In this case, you could also say "Suppose x is an integer." Either way, there is no other restriction on x other than that it is an integer, so it might be even and it might be odd (for example).
Consider the situation in which we want to treat two cases, x being an even integer and x being an odd integer. We begin: "Let x be an integer. Suppose x is even." Later, once we are done with this case, we would then say "Suppose x is odd".
If you wish to treat cases, you do not want to say "Let x be an integer. Let x be even." since the first sentence does not specify what kind of integer x is. Instead, you should write "Let x be an integer. Suppose x is even."
If we were not interested in cases, we could say "Let x be an even integer." - In Problem 2.2, many people made non-statements. If I write "If n=2k, then n is even", then I have not written a statement, since it is not possible to assess the truth of it: we have no idea what k is. If I wrote "If k is an integer and n=2k, then n is even" then I have written a (true) statement.
- Problem 2.4 (c) is a little tricky. We have to treat the statement "xy is even" as "xy is an even integer", so that the negation is "xy is not an even integer". This means "xy is not an integer or xy is an odd integer", and this implies "x or y is not an integer, or both x and y are odd integers."
- In 2.4 (d), the word "but" has the same logical meaning as "and", so the negation of "I will go for a walk but I will not ride my bike" is "I will not go for a walk or I will ride my bike".
- Periods need to be used at the end of every sentence, including ones ending with mathematical expressions. Please write one sentence per line to make commenting and reading easier.
- Do not write a comma where you mean "and". The one exception is with
set inclusion. For example, if we want to indicate that x and y are in the set A,
we can write "x,y ∈ A". But if you want to write that x is in set A and
y is in set B, write "x ∈ A and y ∈ B", not
"x ∈ A, y ∈ B".
This will avoid a lot of confusion and make your writing much stronger.
January 4, 2019
Welcome to Math 300 E, Winter quarter 2019.
Be sure to read the Homework Guidelines pdf before you start thinking about writing up the first homework assignment.
In weeks when homework is due, we will meet on Thursdays from 5:30 to 7:00 PM in PDL C-401 to discuss the homework. This is optional, but highly encouraged, and you may come for all or part of the time.