Tuesday and Thursday 1:30 - 2:45pm in G117 Tompkins Hall

Instructor: Cynthia Vinzant (3260 SAS, email)
Offce Hours: Tuesday 3-4pm, Wednesday 1-2pm or by appointment
Optional Textbook: D. Maclagan and B. Sturmfels, Introduction to Tropical Geometry, Graduate Studies in Mathematics, 161. American Mathematical Society, 2015. (online draft)
Syllabus

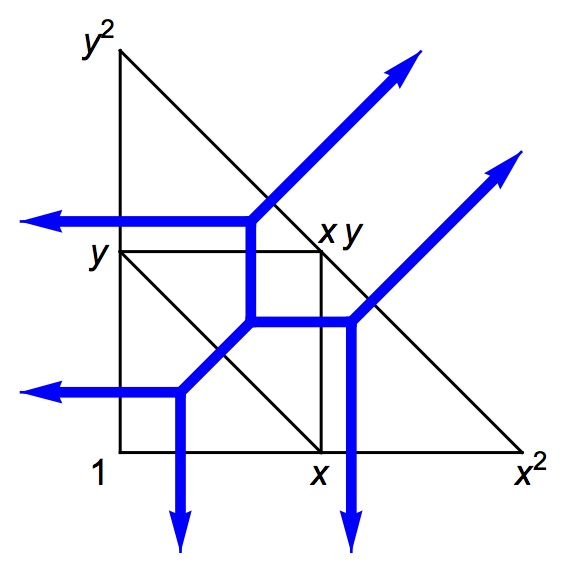
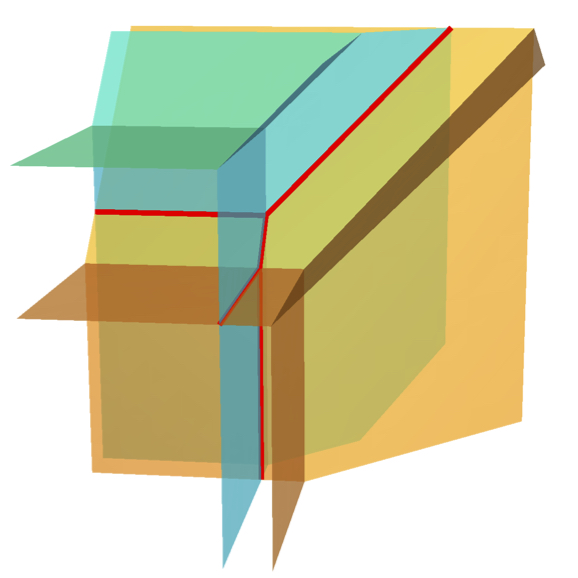
Description: Tropical geometry is the study of certain combinatorial shadows of solutions to systems of polynomial equations. It is based on tropical algebra, where the sum of two numbers is their minimum and the product is their sum. This turns polynomials into piecewise-linear functions, and their zero sets into polyhedral complexes. These combinatorial structures retain a surprising amount of information about their classical counterparts. This course will introduce and survey some topics in tropical geometry, including Puiseux series and valuations, Grobner complexes, tropical varieties, hyperplane arrangements and matroids, tropical convexity, connections with toric varieties, Bernstein's theorem, and Viro's patchworking. Grades will be based on occasional homework assignments and a final project.

Homework
Homework 1 (.pdf .tex) due Thursday, January 28
Homework 2 (.pdf .tex) due Thursday, February 11
Homework 3 (.pdf .tex) due Thursday, February 25
Homework 4 (.pdf .tex) due Tuesday, April 5

Final Project Information
Project choice by March 4
Presentations April 12, 14, 19, 21
Final paper due April 29, 5pm

Presentation Schedule
(April 12) Faye Pasley: The Tropical Commuting Variety
(April 12) Georgy Scholten: The ultimate rank of tropical matrices
(April 14) Dan Bernstein: Subdominant Matroid Ultrametrics
(April 14) Chris Paquette: The Newton polytope of the implicit equation
(April 19) Naomi Boulware: Product Mix Auctions and Tropical Geometry
(April 19) Mike Weselcouch: Discrete concavity and the half-plane property
(April 21) Alex Hazeltine: Bitangents of tropical plane quartic curves
(April 21) Caprice Stanley: Tropical Curves in Sandpiles

Extra reading
What is an Amoeba? by Oleg Viro