
This page has a proof of Napoleon's theorem and also proofs of the main properties of the special ines and circles in this figure that all pass through the Fermat point. The proofs use several important tools that should be reviewed, if needed. See the References section at the end for places to look.
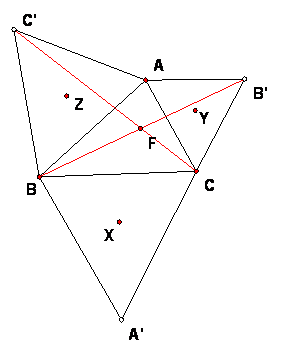
The Napoleon figure is a triangle ABC with an equilateral triangle built on each side: BCA', CAB', ABC'. The centers of the equilateral triangles are X, Y, Z, respectively.

For any triangle ABC, the triangle XYZ is an equilateral triangle.
Proof: The rotation Y120 maps A to C. The rotation X120 maps C to B. So if we define S = X120Y120, then S(A) = X120(Y120(A)) = X120(C) = B.
But by the theory of composition of rotations (see Brown 2.4), S is a rotation by angle 240 degrees and the center D of S is constructed as the vertex of a triangle YXD, where angle X = 120/2 = 60 degrees and angle Y also = 60 degrees. Thus YXD is an equilateral triangle.
But also Z240(A) = B, since Z240 is a symmetry of the triangle ABC'. This means that we now have two rotations, Z240 and D240, and in both cases the image of A is B:
Z240(A) = B
D240(A) = B
But there is only one rotation by 240 degrees that sends A to B. From this relationship, ABZ and ABD are congruent isosceles triangles, with angle Z = angle D = 120 degrees. Since the side AB is shared, either Z = D or Z is the reflection D' of D in AB. But the rotation centered at D' that takes A to B has rotation angle 120, not 240. Thus Z = D and so XYZ is an equilateral triangle.
Study Note: This proof uses two key facts or methods. One is the construction of the center of a rotation obtained by composing two rotations (Brown 2.4). The second is the construction of the center of a rotation if one is given T(A) = B and the rotation angle = x. (See References)
Extensions: This theorem is still true if the triangle ABC is moved so that the points are collinear. If the point C is dragged across AB, then the triangles are all on the inside instead of the outside but triangle XYZ is still equlateral. In fact the transformation proof given here works just as well in those cases.
Theorem: Facts about the Fermat Point
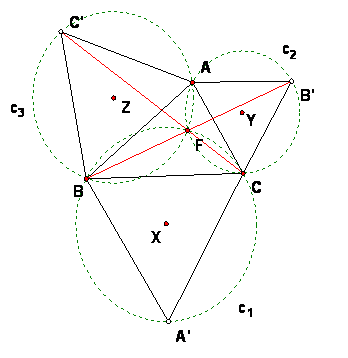
In the same figure construct the segments AA', BB', CC'. Also, let c1, c2, c3 be the circumcircles of the 3 equilateral triangles with centers at X, Y, Z. The following is true:
a) All the segments AA', BB', CC' have the same length.
b) Any two of these segments meet at an angle of 60 degrees.
c) The segments AA', BB', CC' are concurrent at a point F.
d) All the circles c1, c2, c3 are concurrent at F.
Proof:
Proof of (a) and (b): To show that BB' and CC' have the same length and meet at an angle of 60 degrees, it is sufficient to find a rotation by 60 degrees that sends one segment to the other. The rotation A60 does this, for A60(B') = C and A60(B) = C'.
Let F be the intersection of BB' and CC'. Then the segments define angles of 60 degree and 120 degrees since the rotation angle is 60 degrees. (See References.)
The same reasoning with B60 shows that AA' and CC' are congruent and meet at 60 degrees. We do NOT yet know that AA' passes through F.
Proof of (c) and (d):
Consider the 3 circles c1, c2, c3. They all appear to pass through F, but we need to explain why this is true. The reason uses the theory of inscribed angles.
For example, angle C'FB = 60 degrees = angle C'AB. Angle C'AB is an inscribed angle in circle c1. Any point F for which C'FB is also 60 degrees (and which is on the same side of line BC')) must lie on the arc C'AB. (It is clear that if F is on the arc, then the angle C'FB is 60 degrees, but the converse is true also. See References.)
Since angle CFB' = angle CAB', F is also on the arc CAB'.
So we now know that F is on circles c2 and c3. The reason that F is on c1 is slightly different.
Angle BFC = 120 degrees and angle CA'B = 60 degrees. Thus the two angles are supplementary. It is know that any quadrilateral CA'BF with angles A' and F supplementary is a cyclic quadrilateral, i..e., the four vertices all lie on a circle. Thus F is on c3. (Note: This is the inscribed angle locus when the two points A' and F are on the opposite sides of BC.)
Thus F, defined as the intersection of BB' and CC' is the point of concurrence of the 3 circles, c1, c2, c3.
But this proves that F is on AA'. If we started anew and defined G as the intersection of AA' and BB', then we could prove again that G is the point of concurrence of the 3 circles, c1, c2, c3. But this means G = F and so F is on AA' as well. The point F is called the Fermat point of triangle ABC.
So the figure does look like this.
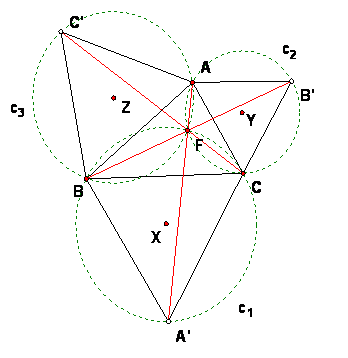
Since all the angles AFB = BFC = BFA = 120 degrees, the Fermat point is the point inside the triangle such that an observer at the point will see the directions towards the 3 vertices appearing equally spaced as she turns around (equal angles of observation, not equal distances of course).
This point turns up in examples with soap films. It is also the point F = P for which the sum of distances |AP| + |BP| + |CP| is a minimum for all P in the triangle.
Study Points: The tools used in this proof included the observation that the angle between a line and a rotated image of the line equals the angle of rotation. The proof also used the locus theorem that is an if and only if theorem about inscribed angles. (See References).
Construcing the center of the rotation X120Y120, (or other compositions of rotations).
Constructing the center of a rotation T given T(A) = B and the angle of rotation of T.
The angle between a line and a its image under rotation is the same as the rotation angle
Generalized Carpenter: Given angle a and points A and B, the locus of points P with angle APB = a consists of an arc on each side of line AB.
Alternate Napoleon and Fermat from Math 487 Aut 2002 Sketchpad Lab
Other References for Fermat Point
Other References for Napoleon's Theorem