From Final Exam 2001

Problem C2: Construction Problem for Isometries

Given points A and B, let S = A₆₀ = rotation by 60 degrees with center A and let T be B₁₂₀ = rotation by 120 degrees with center B. Tell what is U = ST and construct (with straightedge and compass) the geometric data needed to define this transformation directly. (Geometric data means centers, mirror or invariant lines, vectors, etc.)

Answer:

From Brown, 2.4, we see that this composition U is a rotation by 60+120 = 180 degrees, i.e., a half turn C₁₈₀.  What is needed to complete the answer is to construct the point C that is the center of this rotation.

The method explained in Brown is to write S and T as the composition of two lines each, so T = R_m2 R_m1 and S = R_m4 R_m3.  Then U = R_m4 R_m3 R_m2 R_m1.  The trick here is to make m3 and m2 be the same line, so that the product of the middle two reflections is I, the identity, and U =  R_m4 I R_m1 = R_m4 R_m1.   IMPORTANT:  It is critical to get the order of composition right.  In this case of ST is it first B rotation, then A.

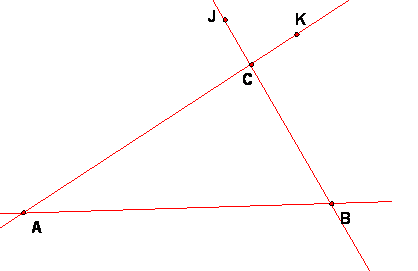
To construct m1 and m2, we let m1 = BJ and m2 = BA, with signed angle JBA = (1/2)120 = 60.  Then m3 = line AB and m4 = line AK, with signed angle BAK = (1/2)60 = 30 degrees. These angles of 60 and 30 degrees can be constructed with straightedge and compass by constructing an equilateral triangle to get an angle of 60 degrees and bisecting this angle to get 30 degrees.

This triangle ABC has angle A = 30 degrees, angle B = 60 degrees and angle C = 90 degrees.  The angle at C is what is expected, for the exterior angle at C should be 180/2 = 90.

This is the answer to the problem, but there is more that we can see in this figure.

Discussion and related practice problems

1. Images of special points

To check that this answer makes sense and is correct, let's check the value of U at some points.  Since we know U is a rotation, the image of two points is enough to identity U.

• U(B) = S(T(B)) = S(B) = B', where B' is the reflection of B in line AC, since then angle BAB' = 60 degrees and |AB| = |AB'|.  But B' is also C₁₈₀(B), the point reflection of B in C.
• U(C) = S(T(C)) = S(C') = C, where C' is the reflection of C in line AB.  The statement U(C) = C is another way to say that C is the center of U.  The statement T(C) = C' is true because angle CBC' = 120 degrees, and |BC| = |BC'|. The statement S(C') = C is true because angle C'AC = 60 degrees and |AC| = |AC'|, S(C') = C.

2. Center of inverse of U

One can use the same method to compute the inverse of U = B_-120 A_-60 = B₂₄₀ A₃₀₀

If you carry this out, you will construct the same triangle.  In this case m1 = line AK, m2 = m3 = line AB and m4 = line BJ.  As should be the case for the inverse of a rotation, the center is the same point C and the angle is -180, which is the same as rotation by +180.

3.  Center of TS

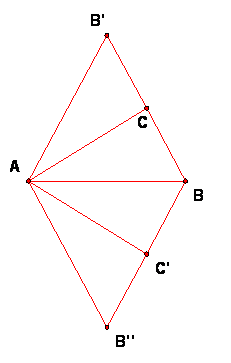
As an exercise, find the center of the rotation V = TS.  It should turn out to be reflection C' of C in AB.  The angle of rotation is still 180 degrees since the sum of the angles is not changed when the order of composition is change.

4.  Center of F = C₁₈₀A₆₀

Find the center of the rotation F = C₁₈₀A₆₀.  You should find that the center is B.  What is the angle of rotation of F?

What rotations centered at B and C can be composed to give a rotation with center A?

5. Relationship with reflected triangles

Reflect B across AC to define B'.  Reflect B' and C across AB to get B'' and C'.  Then check these facts.

• Apply our method to find that A₆₀ C₁₈₀ = B'₂₄₀ = B'_-120. 
• Since C₁₈₀ = A₆₀ A₆₀ B₁₂₀, then B'₂₄₀ = A₆₀ A₆₀ B₁₂₀ = A₁₂₀ B₁₂₀.
• This center B' can also be found by applying the method directly to A₁₂₀ B₁₂₀.
• It is also possible to find this center by checking that A₆₀ C₁₈₀ (B') = B'.
• Likewise, one can find that B'' is the center of B₁₂₀ A₁₂₀.  B'' is also the center of C'₁₈₀ A₆₀
• It was already noted that C'₁₈₀ = B₁₂₀ A₆₀.