Math 487 Lab 10

Topic 1.  A Special Set from Angle Bisector Ratios

Part 1: Construction of D and E.

• Draw points A, B, C and construct LINE (not segment) AB.
• Construct the angle bisector n of angle ACB.  Let D be the intersection of the angle bisector n and line AB.
• Construct the line m as the line through C perpendicular to ray n.  This is the exterior angle bisector line of ACB.  Let E be the intersection of m with line AB.
• Measure ratio CA/CB and also measure ratios DA/DB and EA/EB.
• What is the angle DCE?

Part 2: The set of points with fixed ratio PA/PB.

Question: For a fixed r, what is the set of P for which PA/PB = r?

• Drag C around and see how D and E move on the line AB.  Suppose ratio CA/CB = constant r (such as .25); drag C around trying to keep the ratio the same.  If the ratio stays the same, do D and E move? 
• Can you get a sense the nature of the set of points P with fixed ratio r?  If r = 1, what is the set?  Does the angle DCE give you an idea of what the set is?

IMPORTANT OBSERVATIONS. 

1. If the ratio CA/CB = r, the points D and E are determined by r = DA/DB and EA/EB (there is a difference in sign if we use signed ratios). The points D and E do not depend on which C we choose so long as the ratio = r.
2. For any point P with PA/PB = r = CA/CB, the angle DPE = right angle, so P is on the circle with diameter DE by the Carpenter Locus Theorem.

Construct the set

• Construct the circle c with diameter DE.  Is C on this circle?
• Construct a point P on this circle and measure PA/PB.  Check that the ratio is the same for all P.
• Trace the circle c as you drag the point C.  This shows what all the circles look like.

Conclusion:  For two points A and B and any ratio r > 0, the set of points P with PA/PB = r is a circle (constructed from D and E as above).  This circle is called a circle of Apollonius.

Topic 2:  Napoleon Relations

Make a tool for constructing equilateral triangles ABC with center O given points A and B (i.e., construct the triangle from the edge, but also construct the center and hide the construction lines).

Use this tool to make a Napoleon figure like this one.

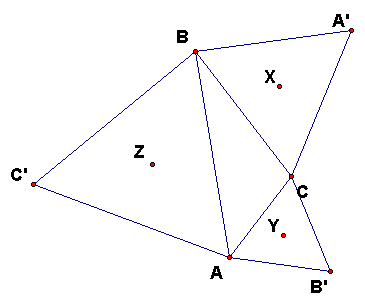
Part 1: Relationship between AA' and BB'

• Draw segment AA'
• Rotate AA' to segment B'B.  To do this, you will need to find a center to mark and choose an angle that will do the job.  It should be clear from your choice that the rotation actually does rotate AA' to B'B.

What is the center?  ______________ .What is the angle? ____________

• Let point P be the intersection of line AA' and line BB'.  Based on the angle of rotation used above, what are the angles that the two lines make at P? (You may want to sketch on a piece of paper the picture of a line and its rotated image with center O. If you construct lines through O parallel to the given line and its image, you will see a rhombus that shows the angle relations needed.)

Answer: Angle BPA' = ________.  Angle BPA = _______.  Angle APB' = _________

Part 2: Enter the circumcircles

• Drag A and B so segments AA' and BB' intersect (not just the lines intersect). 
• Construct the circle with center X through B (circumcircle of BCA'). How is P related to this circle?  How does the value of angle BPA' prove this relationship?

Answer __________________________

• Construct the circle with center Z through A (circumcircle of ABC'). How is P related to this circle?  How does the value of angle APB prove this relationship?

Answer __________________________

• Construct the circle with center Y through C (circumcircle of ACB'). How is P related to this circle?  How does the value of an angle prove this relationship?

Answer __________________________

·        Another case.  Check that if you drag B so that angle ABC > 120 degrees, the circles still are all concurrent at P, but P now lies outside triangle ABC.

Conclusion:  We have seen that P is on all three circles, so the 3 circumcircles are all concurrent at the point of intersection of AA' and BB'.

Part 3:  Relationships among all 3 segments AA', BB', CC'

• Now draw segment CC'. 
• Can you argue that if AA' meets CC' at point Q, that Q must really be P? (Use the circles.)  Conclude that the lines AA', BB', CC' are concurrent at P.
• How are the segment lengths AA', BB', CC' related?
• What are the angles that the 3 lines AA', BB' and CC' make at P? 

The Fermat Point

The Point P is called the Fermat Point of triangle ABC. 

If the angles of ABC are all less than 120 degrees, P lies inside the triangle.  The rays PA, PB, PC all form equal angles of 120 degrees, as we have seen.  This implies that P is the point inside the triangle for which the sum of distances PA + PB + PC is a minimum.  [We are not proving this here.]  See http://www2.evansville.edu/ck6/tcenters/class/fermat.html for some historical background.

Napoleon Invades the Plane

Part 1.  The General Nature of Products of 3 120-degree rotations

We will now investigate the relationship between the Napoleon figure and rotations

• Draw 3 points X, Y, Z on the plane and also draw a point P.
• Rotate P with center X by 120 degrees to get P'.
• Rotate P' with center Y by 120 degrees to get P''.
• Rotate P'' with center Z by 120 degrees to get P'''.
• To visualize the relationship between P and P''', construct the segment PP'''.  Leaving X, Y and Z fixed, drag P around and see how the segment PP''' changes.  Does the length change?  Does the direction change?

Question:  What kind of isometry is the transformation that takes P to P'''.  This isometry is the composition T = Z₁₂₀Y₁₂₀X₁₂₀.

Answer ___________________________

• Move one of X, Y or Z and again observe how PP''' changes as P moves.  Is the transformation still the same kind?  Is it exactly the same transformation?  Can you find a position of Z that approximately doubles |PP'''| from the original value?
• Now our goal is to make P''' coincide with P.  It is does it for one P, then it should do it for any position of P.  Leaving X and Y fixed, drag Z until P''' coincides with P. 

Question: Where is Z when this occurs?

Answer ____________________

• How is this consistent with what we have learned about computing Y₁₂₀X₁₂₀?

Part 2.  Concluding Napoleon's Theorem

Look at the Napoleon figure on the first page. 

• Let P = B in the figure, then P' = A.

What is P'' in this figure? _________________

What is P''' in this figure? _________________

• Since in this figure P = P''', based on your conclusions from the last part, what can you say about the triangle XYZ?

Answer: Triangle XYZ is __________________________________

Draw triangle XYZ in your figure and see that the conclusion appears to be correct as you drag A, B, and C around and XYZ moves in consequence.

Part 3.  Building a Napoleon Figure with Rotations

In a new sketch, draw a point X and a point Y.  Let Z be the rotation of X with center Y by 60 degrees.

• Then draw a point P in the sketch.  Repeat the construction of P', P'', and P''' from Part 1.  You should find that P''' = P, so you can construct segments PP', P'P'', P''P''' form a triangle. (If this does not happen, ask for help!)  Call the points P = B, P' = A, P'' = C so your figure matches the figure on the first page.
• Now construct the 3 equilateral triangles in the figure by rotating appropriate points by 120 degrees with centers X, Y, Z.  Construct the equilateral triangle interiors and color the 3 triangles in 3 different colors.
• You can now drag point B and see how the figure changes with X, Y, and Z immobile.

Part 4.  Covering the plane

• Continuing with this sketch, begin a tessellation of the plane by rotating the whole figure by 120 degrees, first with center X.
• Then select the whole figure and rotate by 120 with center Y.
• Then select the whole figure and rotate by 120 with center Z.
• Then select the whole figure and rotate by 120 with center X.
• Continue until the pattern becomes clear.

Question:  What are the translations that are symmetries of this tessellation?  What is a fundamental region made from triangle ABC and parts of the other triangles that can be used to cover the plane by these translations?

Draw in the Napoleon triangle XYZ and make other copies by the same rotations as above. 

Question: What is a fundamental region for translations made from copies of XYZ?  What does this say about the relationship among the areas of the triangles.