Isometry Constructions from Triangles and Segments

Isometry from a triangle | Orientation-Preserving from Segment | Orientation-reversing from segment

1. How to construct the data of an isometry from the image of a triangle

Given two triangles ABC and A'B'C', we say that a transformation T takes ABC to A'B'C' if T(A) = A' and T(B) = B', and T(C) = C'. If ABC and A'B'C' are congruent triangles, we know from a fundamental theorem on isometries that there is exactly one isometry T that takes ABC to A'B'C'.

Note:  This statement takes into account the order of the vertices. If T takes ABC to A'B'C', then it does not take ABC to C'A'B'.

However, in specific cases, one needs to determine from the two triangles exactly what isometry is T.  What type of isometry is it and what is its defining data.

Construction Method 1: (Use the proof of the fundamental theorem)

A fundamental theorem is proved that a triangle ABC can be transformed to a congruent triangle A'B'C' by the composition of one, two or three line reflections.  Thus the isometry T that takes ABC to A'B'C' is this composition. The proof is a step by step construction of up to three lines of reflection.  One can make this construction and then use the theorems about composition of isometries to determine exactly what isometry is T. However, this method is long and indirect, especially for glide reflections.

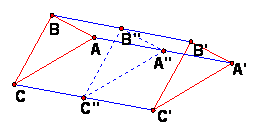
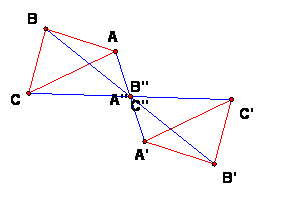
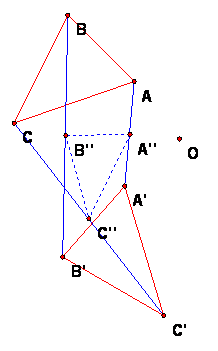
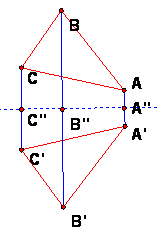
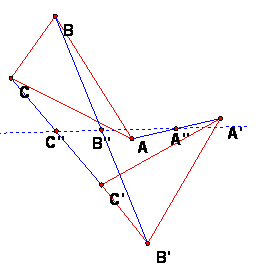
Construction Method 2:  (Use midpoints)

Given two congruent triangles ABC and A'B'C', construct the midpoints A'' of AA', B'' of BB', C'' of CC'. 

Then the arrangement of the midpoints will tell what kind of isometry T takes ABC to A'B'C'.

  1. If T is the identity or a translation, A''B''C'' is a triangle congruent to ABC.
  2. If T is a rotation by angle x but not a halfturn, then A''B''C'' is a triangle similar to ABC (the scaling factor is cos(x/2).
  3. If T is a half turn, the 3 midpoints are all the same point, which is the center of the halfturn.
  4. If T is a line reflection, the 3 midpoints are collinear and at most 2 coincide, since A, B, C are not collinear*.  Thus there is one line through the midpoints, and this is the mirror line of T.
  5. If T is a glide reflection, the 3 midpoints are collinear and at most 2 coincide, since A, B, C are not collinear*. Thus there is one line through the midpoints, and this is the invariant line of T.

Translation

Halfturn

Rotation

Line Reflection

Glide Reflection

* The proof that the points A'', B'' and C'' cannot all be the same for a line reflection or a glide reflection follows from the definitions of these transformations.  For T = a line reflection in a line m, A'', B'', C'' are the feet of the perpendiculars to m through A, B, C.  Thus they can only coincide if A, B, C are all on the same line perpendicular to m.  For T = glide reflection with glide vector v, then if A*, B*, C* are the feet of the perpendiculars to m through A, B, C, then A'', B'', C'' are the translations of these points by vector (1/2)v. Thus the midpoints A'', B'', C'' coincide if and only if the feet A*, B*, C* coincide, which means again that A, B, C are all on the same line perpendicular to m. 

These cases allow us to deduce the nature of the isometry from the midpoints A''B''C''.

  1. If the points coincide with a point P, T is a halfturn with center P.
  2. If the points are collinear, but do not all coincide, then T is orientation reversing.  Complete the construction of the geometric data is spelled out in this section below: Construction Method: Line reflection or glide reflection from 2 congruent segments
  3. If the points form a triangle, then T is orientation preserving, and the data can be constructed by the description in this section below: Construction Method: Rotation or translation from 2 congruent segments

2. How to construct the data of a rotation or translation from the image of a segment or a point

Fundamental Theorem | From Image of a Segment | From Image of a Point knowing Angle

Given two segments AB and CD, we say that a transformation T takes AB to CD if T(A) = C and T(B) = D. 

Note:  This statement takes into account the order of the endpoints. If T takes AB to CD, then it does not take AB to DC.

Theorem (Fundamental Theorem for Orientation-Preserving Isometries)

Given two congruent segments AB and CD, there is exactly one orientation-preserving isometry T that takes AB to CD.

Proof (also a construction): 

This consists of the first two steps of the Second Fundamental Theorem of Isometries.

When A and C are distinct, let m1 be the perpendicular bisector of AC. In the special case where A = C, let m1 = line AB (actually, any line through A will do). Let R1 denote line reflection in m1. 

For this reflection, R1(A) = C.  Let B' = R1(B).  Segment CD is congruent to CB' since R1 is an isometry.

If B' is not D, let m2 be the perpendicular bisector of B'D.  Since |CB'| = |CD|, the point C is on m2.  In the special case B' = D, let m2 = line CD. Let R2 be reflection in m2.

In either case, R2(B') = D and R2(C) = C.  So setting T = R2R1, T(A) = C and T(B) = D.

T is the composition of two line reflections. T is a rotation with center O if the two lines m1 and m2 intersect in one point O; it is a translation if m1 and m2 are parallel. If the lines are the same, then T is the identity.

Finally, it is claimed that T is the only orientation-preserving isometry that takes AB to CD.  To see this, assume that S = R4R3 also takes AB to CD.  Then S-1  = R3R4 takes CD to AD.  Thus S-1T = R3R4R2R1 takes AB to AB. 

This means that S-1T (A) = A and S-1T (B) = B are two fixed points of the isometry.  But the isometry S-1T is an orientation-preserving isometry, since it is the product of 4 line reflections.  This means that it is a rotation, a translation, or the identity.  But the only one of these isometries with two fixed points is the identity, so S-1T = I, and so T = S.

Thus there is only one orientation-preserving isometry that takes AB to CD.

Construction Method: Rotation or translation from 2 congruent segments

Given two congruent segments AB and CD, how can one construct the unique orientation-preserving isometry T that takes AB to CD?

In practice, the cases of interest are when T is a rotation or a translation, since if A = C and B = D, no construction is necessary for the identity.

General Case:  Assume A is not C and B is not D. Construct the lines m = perpendicular bisector of AC and n = perpendicular bisector of BD.

If T is a rotation, the lines m and n intersect at O, the center of the rotation.  For in this case A and C = T(A) are both on the same circle with center O, so the bisector m of the chord AC passes through O.  For the same reason, n passes through O.  The angle of the rotation is angle AOC.

In the special case of a halfturn, O is also the midpoint of AC and BD as well as the intersection of m and n.

If T is a translation, then AC and BD are parallel, so m and n are also parallel.  The translation vector is AC.

Special cases:  Assume A = C but B and D are distinct. In this case, A is already the center of a rotation that will take B to D.   The rotation angle is angle BAD.  The case when B = D is handled in the same way.  If A = C and B = D, then T = identity.

Construction Method:  Rotation from image of one point plus the rotation angle

Suppose that T is known to be a rotation by angle x.  If we are given two distinct points A and C, such that T(A) = C, is this enough to determine T?

 

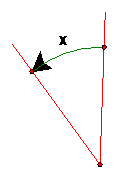
Since the rotation angle of T is given, if the center O can be constructed, then T will be known completely. 

From the given information T(A) = C, it follows that O is on the line m, the perpendicular bisector of AC.  Also, angle AOC = x. 

The angle x is an oriented, or signed angle.  There are several cases:

  1. Angle x = 0 degrees. This means T = I and so A = T(A) = C.  This violates the assumption that A and C are distinct.
  2. Angle x = 180 degrees.  In this case T is a halfturn and O = midpoint AC.  This completes the construction.
  3. For angle x, 0 < x < 180.  This will be discussed below
  4. For angle x, -180 < x < 0.  This is much like case 3, and will be discussed below.

Cases 3 and 4: In each case, 0 < |x| < 180 is the unoriented angle AOC.

Imagine that O has been constructed.  Then OA = OC, since T is a rotation with center O.  Also, angle AOC = x.  This means that triangle OAC is an isosceles triangle with (unoriented) angle O = |x|, and angle A = angle C = y = (180-|x|)/2 = 90 – (|x|/2).

So to construct such a triangle, it is only necessary to construct a ray AD so that angle CAD = y.  Intersect this ray with m to get P. 

Reflect P in line AC to get Q.  Then both triangles PAC and QAC are isosceles triangles with (unoriented) angles |x|, y, y.  One of the angles APC or AQC is +|x| and the other is -|x|.  So one is the solution to case 3 and one is the solution to case 4.

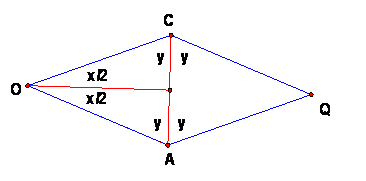
It is clear from this construction that there is only one T for each (oriented) x.

 To construct the angle y, it is only necessary to construct an isosceles triangle with angles |x|, y, y and copy the angle y.  For example, suppose that angle FGH = |x| is given.  Then choose some point K on ray GF and let the point L on GH be that point with |GL| = |GK|.  This means that GKL is an isosceles triangle with angles |x|, y, y.

This completes the construction, and also proves the theorem that for any distinct A and C and any oriented, non-zero angle, there is a unique rotation that takes A to C with this angle of rotation

Other constructions:  Translation or Halfturn from image of one point

Given two distinct points A and C, there is a unique Halfturn H that takes A to C.

The construction of the center O of the halfturn is simple.  O is the midpoint of AC.  For any other point B, H(B) is the point D for which O is the midpoint of BD.

Given two distinct points A and C, there is a unique translation T that takes A to C.

The translation vector is AC.  Thus for any B not on line AC, T(B) is the point D such that ACDB is an parallelogram.  If B is on line AC, then this alternative criterion for parallelogram still works.  D is the point so that the midpoint of AD = the midpoint of BC.

3. How to construct the data of a line reflection or glide reflection from the image of a segment or a point

Fundamental Theorem | From Image of a Segment | From Image of a Point Knowing Vector

Recall our definition: Given two segments AB and CD, we say that a transformation T takes AB to CD if T(A) = C and T(B) = D. 

Note:  This statement takes into account the order of the endpoints. If T takes AB to CD, then it does not take AB to DC.

Theorem (Fundamental Theorem for Orientation-Reversing Isometries)

Given two congruent segments AB and CD, there is exactly one orientation-reversing isometry U that takes AB to CD.

Proof: This follows from the theorem for orientation-preserving isometries

Given AB and CD, there is exactly one orientation-preserving isometry T that takes AB to CD.  Let R = line reflection in AB.  Then U = RT is an orientation-reversing isometry that takes AB to CD.  This shows that U exists.

To see that there is only one such U, suppose that V is another orientation-reversing isometry that takes AB to CD.  Then RV is an orientation preserving isometry that takes AB to CD, and so RV must = T.  Then V = RRV = RT.  But by definition, RT = U.

QED

Construction Method: Line reflection or glide reflection from 2 congruent segments

Given two congruent segments AB and CD, how can one construct the unique orientation-reversing isometry U that takes AB to CD?

From the definitions of line reflection and a theorem about glide reflection, for any orientation-reversing U and for any point A and C = U(A), the midpoint of AC is on the mirror line (if U is a line reflection) or the invariant line (if U is a glide reflection).

Thus if U takes AB to CD, let M = midpoint AC and N = midpoint BD.

Let A' and B' be the reflections of A and B in line MN.

If U is a line reflection, then the segments AC and BD are both perpendicular to MN and in fact MN is the perpendicular bisector of these two segments.  In this case A' = C and B' = D.

 

If U is a glide reflection, MN is the invariant line.  Neither of the segments AC and BD will be perpendicular to MN.  The glide vector = A'C = B'D.

To construct the image of some other point P, reflect P in line MN to get P' and then translate by the glide vector.

Construction Method: Line reflection or glide reflection from the image of one point plus glide vector

Suppose that U is known to be either (a) a line reflection or (b) a glide reflection with given glide vector EF. Given two distinct points A and C, how can one construct the unique orientation-reversing isometry U that takes A to C?

First, if U is a line reflection, then let m be the perpendicular bisector of AC.  Then U is line reflection in m.

Second, if EF is given, let A' be the translation of C by vector FE = -EF.  By the definition of the glide vector, then the perpendicular bisector n of AA' must be the invariant line of U and U = TEFRn.