• Home
• Research
• Teaching
• Links

Farbod Shokrieh - Research

---

MathSciNet profile
Google Scholar profile
arXiv preprints

My work is partially supported by NSF CAREER DMS-2044564

Publications:

• Jumps in the height of the Ceresa cycle. (with Robin de Jong)
  • Journal of Differential Geometry, Volume 126, No. 1, Pages 169-214, 2024.
  • abstract | DOI | arXiv | bibtex

We study the jumps in the archimedean height of the Ceresa cycle, as introduced by R. Hain in his work on normal functions on moduli spaces of curves, and as further analyzed by P. Brosnan and G. Pearlstein in terms of asymptotic Hodge theory. Our work is based on a study of the asymptotic behavior of the Hain-Reed beta-invariant in degenerating families of curves. We show that the height jump of the Ceresa cycle at a given stable curve is equal to the so-called "slope" of the dual graph of the curve, and we characterize those stable curves for which the height jump vanishes. We also obtain an analytic formula for the height of the Ceresa cycle for a curve over a function field over the complex numbers, and characterize in analytic terms when the height of the Ceresa cycle vanishes.

@article {MR4704548,
    AUTHOR = {de Jong, Robin and Shokrieh, Farbod},
     TITLE = {Jumps in the height of the {C}eresa cycle},
   JOURNAL = {J. Differential Geom.},
  FJOURNAL = {Journal of Differential Geometry},
    VOLUME = {126},
      YEAR = {2024},
    NUMBER = {1},
     PAGES = {169--214},
      ISSN = {0022-040X,1945-743X},
   MRCLASS = {14C30 (14D07 14G40 14H15 14T20 32G20)},
  MRNUMBER = {4704548},
       DOI = {10.4310/jdg/1707767337},
       URL = {https://doi.org/10.4310/jdg/1707767337},
}



• A sheaf-theoretic approach to tropical homology. (with Andreas Gross)
  • Journal of Algebra, Volume 635, Pages 577-641, 2023.
  • abstract | DOI | arXiv | bibtex

We introduce a sheaf-theoretic approach to tropical homology, especially for tropical homology with potentially non-compact supports. Our setup is suited to study the functorial properties of tropical homology, and we show that it behaves analogously to classical Borel-Moore homology in the sense that there are proper push-forwards, cross products, and cup products with tropical cohomology classes, and that it satisfies identities like the projection formula and the Künneth theorem. Our framework allows for a natural definition of the tropical cycle class map, which we show to be a natural transformation. Finally, we characterize the rational polyhedral spaces that satisfy Poincaré-Verdier duality as those that are smooth.

@article {MR4637248,
    AUTHOR = {Gross, Andreas and Shokrieh, Farbod},
     TITLE = {A sheaf-theoretic approach to tropical homology},
   JOURNAL = {J. Algebra},
  FJOURNAL = {Journal of Algebra},
    VOLUME = {635},
      YEAR = {2023},
     PAGES = {577--641},
      ISSN = {0021-8693,1090-266X},
   MRCLASS = {14C17 (14C25 52B40)},
  MRNUMBER = {4637248},
       DOI = {10.1016/j.jalgebra.2023.08.014},
       URL = {https://doi.org/10.1016/j.jalgebra.2023.08.014},
}



• Torsor structures on spanning trees. (with Cameron Wright)
  • SIAM Journal on Discrete Mathematics, Volume 37, No. 3, Pages 2126-2147, 2023.
  • abstract | DOI | arXiv | bibtex

We study two actions of the (degree ) Picard group on the set of the spanning trees of a finite ribbon graph. It is known that these two actions, denoted and respectively, are independent of the base vertex if and only if the ribbon graph is planar. Baker and Wang conjectured that, in a nonplanar ribbon graph without multiple edges, there always exists a vertex for which . We prove the conjecture and extend it to a class of ribbon graphs with multiple edges. We also give explicit examples exploring the relationship between the two torsor structures in the nonplanar case.

@article {MR4643471,
    AUTHOR = {Shokrieh, Farbod and Wright, Cameron},
     TITLE = {On {T}orsor {S}tructures on {S}panning {T}rees},
   JOURNAL = {SIAM J. Discrete Math.},
  FJOURNAL = {SIAM Journal on Discrete Mathematics},
    VOLUME = {37},
      YEAR = {2023},
    NUMBER = {3},
     PAGES = {2126--2147},
      ISSN = {0895-4801,1095-7146},
   MRCLASS = {99-06},
  MRNUMBER = {4643471},
       DOI = {10.1137/22M149154X},
       URL = {https://doi.org/10.1137/22M149154X},
}



• Tropical moments of tropical Jacobians. (with Robin de Jong)
  • Canadian Journal of Mathematics, Volume 75, Issue 4, Pages 1045-1075, 2023.
  • abstract | DOI | arXiv | bibtex

Each metric graph has canonically associated to it a polarized real torus called its tropical Jacobian. A fundamental real-valued invariant associated to each polarized real torus is its tropical moment. We give an explicit and efficiently computable formula for the tropical moment of a tropical Jacobian in terms of potential theory on the underlying metric graph. We show that there exists a universal linear relation between the tropical moment, a certain capacity called the tau invariant, and the total length of a metric graph. To put our formula in a broader context, we relate our work to the computation of heights attached to principally polarized abelian varieties.

@article {MR4620315,
    AUTHOR = {de Jong, Robin and Shokrieh, Farbod},
     TITLE = {Tropical moments of tropical {J}acobians},
   JOURNAL = {Canad. J. Math.},
  FJOURNAL = {Canadian Journal of Mathematics. Journal Canadien de
              Math\'{e}matiques},
    VOLUME = {75},
      YEAR = {2023},
    NUMBER = {4},
     PAGES = {1045--1075},
      ISSN = {0008-414X,1496-4279},
   MRCLASS = {99-06},
  MRNUMBER = {4620315},
       DOI = {10.4153/s0008414x22000220},
       URL = {https://doi.org/10.4153/s0008414x22000220},
}



• Tautological cycles on tropical Jacobians. (with Andreas Gross)
  • Algebra & Number Theory, Volume 17, Issue 4, Pages 885-921, 2023.
  • abstract | DOI | arXiv | bibtex

The classical Poincaré formula relates the rational homology classes of tautological cycles on a Jacobian to powers of the class of Riemann theta divisor. We prove a tropical analogue of this formula. Along the way, we prove several foundational results about real tori with integral structures (and, therefore, tropical abelian varieties). For example, we prove a tropical version of the Appell-Humbert theorem. We also study various notions of equivalences between tropical cycles and their relation to one another.

@article {MR4582532,
    AUTHOR = {Gross, Andreas and Shokrieh, Farbod},
     TITLE = {Tautological cycles on tropical {J}acobians},
   JOURNAL = {Algebra Number Theory},
  FJOURNAL = {Algebra \& Number Theory},
    VOLUME = {17},
      YEAR = {2023},
    NUMBER = {4},
     PAGES = {885--921},
      ISSN = {1937-0652,1944-7833},
   MRCLASS = {14T20 (14H40 14H42 14H51)},
  MRNUMBER = {4582532},
       DOI = {10.2140/ant.2023.17.885},
       URL = {https://doi.org/10.2140/ant.2023.17.885},
}



• Faltings height and Néron-Tate height of a theta divisor. (with Robin de Jong)
  • Compositio Mathematica, Volume 158, Issue 1, Pages 1-32, 2022.
  • abstract | DOI | arXiv | bibtex

We prove a formula which, given a principally polarized abelian variety over the field of algebraic numbers, relates the stable Faltings height of with the Néron-Tate height of a symmetric theta divisor on . Our formula completes earlier results due to Bost, Hindry, Autissier and Wagener. The local non-archimedean terms in our formula can be expressed as the tropical moments of the tropicalizations of .

@article {MR4371040,
    AUTHOR = {de Jong, Robin and Shokrieh, Farbod},
     TITLE = {Faltings height and {N}\'{e}ron-{T}ate height of a theta divisor},
   JOURNAL = {Compos. Math.},
  FJOURNAL = {Compositio Mathematica},
    VOLUME = {158},
      YEAR = {2022},
    NUMBER = {1},
     PAGES = {1--32},
      ISSN = {0010-437X},
   MRCLASS = {11G10 (11G50 14G40 14K25)},
  MRNUMBER = {4371040},
       DOI = {10.1112/s0010437x21007661},
       URL = {https://doi.org/10.1112/s0010437x21007661},
}



• Metric graphs, cross ratios, and Rayleigh's laws. (with Robin de Jong)
  • Rocky Mountain Journal of Mathematics, Volume 52, Number 4, Pages 1403-1422, 2022.
  • abstract | DOI | arXiv | bibtex

We systematically study the notion of cross ratios and energy pairings on metric graphs and electrical networks. We show that several foundational results on electrical networks and metric graphs immediately follow from the basic properties of cross ratios. For example, the projection matrices of Kirchhoff have natural (and efficiently computable) expressions in terms of cross ratios. We prove a generalized version of Rayleigh's law, relating energy pairings and cross ratios on metric graphs before and after contracting an edge segment. Quantitative versions of the Rayleigh's law for effective resistances, potential kernels, and cross ratios will follow as immediate corollaries.

@article {MR4489167,
    AUTHOR = {de Jong, Robin and Shokrieh, Farbod},
     TITLE = {Metric graphs, cross ratios, and {R}ayleigh's laws},
   JOURNAL = {Rocky Mountain J. Math.},
  FJOURNAL = {The Rocky Mountain Journal of Mathematics},
    VOLUME = {52},
      YEAR = {2022},
    NUMBER = {4},
     PAGES = {1403--1422},
      ISSN = {0035-7596},
   MRCLASS = {Prelim},
  MRNUMBER = {4489167},
       DOI = {10.1216/rmj.2022.52.1403},
       URL = {https://doi-org.offcampus.lib.washington.edu/10.1216/rmj.2022.52.1403},
}



• Effective divisor classes on metric graphs. (with Andreas Gross and Lilla Tóthmérész)
  • Mathematische Zeitschrift, Volume 302, Number 2, Pages 663-685, 2022.
  • abstract | DOI | arXiv | bibtex | free (view-only)

We introduce the notion of semibreak divisors on metric graphs and prove that every effective divisor class (of degree at most the genus) has a semibreak divisor representative. This appropriately generalizes the notion of break divisors (in degree equal to genus). We provide an algorithm to efficiently compute such semibreak representatives. Semibreak divisors provide the tool to establish some basic properties of effective loci inside Picard groups of metric graphs. We prove that effective loci are pure-dimensional polyhedral sets. We also prove that a 'generic' divisor class (in degree at most the genus) has rank zero, and that the Abel-Jacobi map is 'birational' onto its image. These are analogues of classical results for Riemann surfaces.

@article {MR4480205,
    AUTHOR = {Gross, Andreas and Shokrieh, Farbod and T\'{o}thm\'{e}r\'{e}sz, Lilla},
     TITLE = {Effective divisor classes on metric graphs},
   JOURNAL = {Math. Z.},
  FJOURNAL = {Mathematische Zeitschrift},
    VOLUME = {302},
      YEAR = {2022},
    NUMBER = {2},
     PAGES = {663--685},
      ISSN = {0025-5874},
   MRCLASS = {14T90 (05C25)},
  MRNUMBER = {4480205},
       DOI = {10.1007/s00209-022-03056-x},
       URL = {https://doi-org.offcampus.lib.washington.edu/10.1007/s00209-022-03056-x},
}



• Cycles, cocycles, and duality on tropical manifolds. (with Andreas Gross)
  • Proceedings of the AMS, Volume 149, Number 6, Pages 2429-2444, 2021.
  • abstract | DOI | arXiv | bibtex

We prove a Poincaré duality for the Chow rings of smooth fans whose support are tropical linear spaces. As a consequence, we show that cycles and cocycles on tropical manifolds are Poincaré dual to each other. This allows us to define pull-backs of tropical cycles along arbitrary morphisms with smooth target.

@article {MR4246795,
    AUTHOR = {Gross, Andreas and Shokrieh, Farbod},
     TITLE = {Cycles, cocycles, and duality on tropical manifolds},
   JOURNAL = {Proc. Amer. Math. Soc.},
  FJOURNAL = {Proceedings of the American Mathematical Society},
    VOLUME = {149},
      YEAR = {2021},
    NUMBER = {6},
     PAGES = {2429--2444},
      ISSN = {0002-9939},
   MRCLASS = {14T10 (05B35 14C17)},
  MRNUMBER = {4246795},
       DOI = {10.1090/proc/15468},
       URL = {https://doi.org/10.1090/proc/15468},
}



• Limits of canonical forms on towers of Riemann surfaces. (with Hyungryul Baik and Chenxi Wu)
  • Journal für die reine und angewandte Mathematik (Crelle's Journal), Volume 764, Pages 287-304, 2020.
  • abstract | DOI | arXiv | bibtex

We prove a generalized version of Kazhdan's theorem for canonical forms on Riemann surfaces. In the classical version, one starts with an ascending sequence of finite Galois covers of a hyperbolic Riemann Surface , converging to the universal cover. The theorem states that the sequence of forms on inherited from the canonical forms on 's converges uniformly to (a multiple of) the hyperbolic form. We prove a generalized version of this theorem, where the universal cover is replaced with any infinite Galois cover. Along the way, we also prove a Gauss--Bonnet type theorem in the context of arbitrary infinite Galois covers.

@article {MR4116639,
    AUTHOR = {Baik, Hyungryul and Shokrieh, Farbod and Wu, Chenxi},
     TITLE = {Limits of canonical forms on towers of {R}iemann surfaces},
   JOURNAL = {J. Reine Angew. Math.},
  FJOURNAL = {Journal f\"{u}r die Reine und Angewandte Mathematik. [Crelle's Journal]},
    VOLUME = {764},
      YEAR = {2020},
     PAGES = {287--304},
      ISSN = {0075-4102},
   MRCLASS = {30F10 (14H30 57K20)},
  MRNUMBER = {4116639},
       DOI = {10.1515/crelle-2019-0007},
       URL = {https://doi.org/10.1515/crelle-2019-0007},
}



• Canonical measures on metric graphs and a Kazhdan's theorem. (with Chenxi Wu)
  • Inventiones mathematicae, Volume 215, Issue 3, Pages 819-862, 2019.
  • abstract | DOI | arXiv | bibtex | free (view-only)

We extend the notion of canonical measures to all (possibly non-compact) metric graphs. This will allow us to introduce a notion of hyperbolic measures on universal covers of metric graphs. Kazhdan's theorem for Riemann surfaces describes the limiting behavior of canonical (Arakelov) measures on finite covers in relation to the hyperbolic measure. We will prove a generalized version of this theorem for metric graphs, allowing any infinite Galois cover to replace the universal cover. We will show all such limiting measures satisfy a version of Gauss-Bonnet formula which, using the theory of von Neumann dimensions, can be interpreted as a trace formula. In the special case where the infinite cover is the universal cover, we will provide explicit methods to compute the corresponding limiting (hyperbolic) measure. Our ideas are motivated by non-Archimedean analytic and tropical geometry.

@article {MR3935033,
    AUTHOR = {Shokrieh, Farbod and Wu, Chenxi},
     TITLE = {Canonical measures on metric graphs and a {K}azhdan's theorem},
   JOURNAL = {Invent. Math.},
  FJOURNAL = {Inventiones Mathematicae},
    VOLUME = {215},
      YEAR = {2019},
    NUMBER = {3},
     PAGES = {819--862},
      ISSN = {0020-9910},
   MRCLASS = {14T05 (05C12 05C63 14H30 20F65 57M60)},
  MRNUMBER = {3935033},
MRREVIEWER = {Hannah Markwig},
       DOI = {10.1007/s00222-018-0838-5},
       URL = {https://doi.org/10.1007/s00222-018-0838-5},
}



• Non-Archimedean and tropical theta functions. (with Tyler Foster, Joseph Rabinoff, and Alejandro Soto)
  • Mathematische Annalen, Volume 372, Issue 3-4, Pages 891-914, 2018.
  • abstract | DOI | arXiv | bibtex | free (view-only)

We define a tropicalization procedure for theta functions on abelian varieties over a non-Archimedean field. We show that the tropicalization of a non-Archimedean theta function is a tropical theta function, and that the tropicalization of a non-Archimedean Riemann theta function is a tropical Riemann theta function, up to scaling and an additive constant. We apply these results to the construction of rational functions with prescribed behavior on the skeleton of a principally polarized abelian variety. We work with the Raynaud--Bosch--Lütkebohmert theory of non-Archimedean theta functions for abelian varieties with semi-abelian reduction.

@article {MR3880286,
    AUTHOR = {Foster, Tyler and Rabinoff, Joseph and Shokrieh, Farbod and Soto, Alejandro},
     TITLE = {Non-{A}rchimedean and tropical theta functions},
   JOURNAL = {Math. Ann.},
  FJOURNAL = {Mathematische Annalen},
    VOLUME = {372},
      YEAR = {2018},
    NUMBER = {3-4},
     PAGES = {891--914},
      ISSN = {0025-5831},
   MRCLASS = {14T05 (14K25)},
  MRNUMBER = {3880286},
MRREVIEWER = {Shu Kawaguchi},
       DOI = {10.1007/s00208-018-1646-3},
       URL = {https://doi.org/10.1007/s00208-018-1646-3},
}



• Divisors on graphs, binomial and monomial ideals, and cellular resolutions. (with Fatemeh Mohammadi)
  • Mathematische Zeitschrift, Volume 283, Issue 1, Pages 59-102, 2016.
  • abstract | DOI | arXiv | bibtex | free (view-only)

We study various binomial and monomial ideals arising in the theory of divisors, orientations, and matroids on graphs. We use ideas from potential theory on graphs and from the theory of Delaunay decompositions for lattices to describe their minimal polyhedral cellular free resolutions. We show that the resolutions of all these ideals are closely related and that their 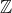-graded Betti tables coincide. As corollaries, we give conceptual proofs of conjectures and questions posed by Postnikov and Shapiro, by Manjunath and Sturmfels, and by Perkinson, Perlman, and Wilmes. Various other results related to the theory of chip-firing games on graphs also follow from our general techniques and results.

@article {MR3489059,
    AUTHOR = {Mohammadi, Fatemeh and Shokrieh, Farbod},
     TITLE = {Divisors on graphs, binomial and monomial ideals, and cellular resolutions},
   JOURNAL = {Math. Z.},
  FJOURNAL = {Mathematische Zeitschrift},
    VOLUME = {283},
      YEAR = {2016},
    NUMBER = {1-2},
     PAGES = {59--102},
      ISSN = {0025-5874},
   MRCLASS = {13D02 (05C25 52C07)},
  MRNUMBER = {3489059},
MRREVIEWER = {Sara Saeedi Madani},
       DOI = {10.1007/s00209-015-1589-2},
       URL = {https://doi.org/10.1007/s00209-015-1589-2},
}



• Canonical representatives for divisor classes on tropical curves and the Matrix-Tree Theorem. (with Yang An, Matthew Baker, and Greg Kuperberg)
  • Forum of Mathematics, Sigma, Volume 2, 25 pages, 2014.
  • abstract | DOI | arXiv | bibtex

Let be a compact tropical curve (or metric graph) of genus . Using the theory of tropical theta functions, Mikhalkin and Zharkov proved that there is a canonical effective representative for each linear equivalence class of divisors of degree on . We characterize these canonical effective representatives as the set of break divisors on and present a new combinatorial proof that there is a unique break divisor in each equivalence class. We also establish the closely related fact that for fixed in , every divisor of degree is linearly equivalent to a unique -orientable divisor. For both of these results, we also prove discrete versions for finite unweighted graphs which do not follow from the results of Mikhalkin-Zharkov. As an application of the theory of break divisors, we provide a "geometric proof" of (a dual version of) Kirchhoff's celebrated Matrix-Tree Theorem. Indeed, we show that each weighted graph model for gives rise to a canonical polyhedral decomposition of the -dimensional real torus into parallelotopes , one for each spanning tree of , and the dual Kirchhoff theorem becomes the statement that the volume of is the sum of the volumes of the cells in the decomposition.

@article {MR3264262,
    AUTHOR = {An, Yang and Baker, Matthew and Kuperberg, Greg and Shokrieh, Farbod},
     TITLE = {Canonical representatives for divisor classes on tropical curves and the matrix-tree theorem},
   JOURNAL = {Forum Math. Sigma},
  FJOURNAL = {Forum of Mathematics. Sigma},
    VOLUME = {2},
      YEAR = {2014},
     PAGES = {Paper No. e24, 25},
   MRCLASS = {14T05 (05A19 05C25 05E45 14C20)},
  MRNUMBER = {3264262},
MRREVIEWER = {Luis Felipe Tabera},
       DOI = {10.1017/fms.2014.25},
       URL = {https://doi.org/10.1017/fms.2014.25},
}



• Divisors on graphs, connected flags, and syzygies. (with Fatemeh Mohammadi)
  • International Mathematics Research Notices (IMRN), no. 24, Pages 6839-6905, 2014.
  • abstract | DOI | arXiv | bibtex | extended abstract (appeared in FPSAC '13)

We study the binomial and monomial ideals arising from linear equivalence of divisors on graphs from the point of view of Gröbner theory. We give an explicit description of a minimal Gröbner basis for each higher syzygy module. In each case the given minimal Gröbner basis is also a minimal generating set. The Betti numbers of the binomial ideal and its natural initial ideal coincide and they correspond to the number of connected flags in the graph. In particular the Betti numbers are independent of the characteristic of the base field. For complete graphs the problem was previously studied by Postnikov and Shapiro and by Manjunath and Sturmfel. The case of a general graph was stated as an open problem.

@article {MR3291642,
    AUTHOR = {Mohammadi, Fatemeh and Shokrieh, Farbod},
     TITLE = {Divisors on graphs, connected flags, and syzygies},
   JOURNAL = {Int. Math. Res. Not. IMRN},
  FJOURNAL = {International Mathematics Research Notices. IMRN},
      YEAR = {2014},
    NUMBER = {24},
     PAGES = {6839--6905},
      ISSN = {1073-7928},
   MRCLASS = {13F20 (05C25 13D02 13P10)},
  MRNUMBER = {3291642},
MRREVIEWER = {Yuehui Zhang},
       DOI = {10.1093/imrn/rnt186},
       URL = {https://doi.org/10.1093/imrn/rnt186},
}



• Chip-firing games, potential theory on graphs, and spanning trees. (with Matthew Baker)
  • Journal of Combinatorial Theory, Series A, Volume 120, Issue 1, Pages 164-182, 2013.
  • abstract | DOI | arXiv | bibtex

We study the interplay between chip-firing games and potential theory on graphs, characterizing reduced divisors (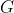-parking functions) on graphs as the solution to an energy (or potential) minimization problem and providing an algorithm to efficiently compute reduced divisors. Applications include an efficient bijective proof of Kirchhoff's matrix-tree theorem and a new algorithm for finding random spanning trees. The running times of our algorithms are analyzed using potential theory, and we show that the bounds thus obtained generalize and improve upon several previous results in the literature.

@article {MR2971705,
    AUTHOR = {Baker, Matthew and Shokrieh, Farbod},
     TITLE = {Chip-firing games, potential theory on graphs, and spanning trees},
   JOURNAL = {J. Combin. Theory Ser. A},
  FJOURNAL = {Journal of Combinatorial Theory. Series A},
    VOLUME = {120},
      YEAR = {2013},
    NUMBER = {1},
     PAGES = {164--182},
      ISSN = {0097-3165},
   MRCLASS = {05C57 (05C05 05C50 31C20 65R10)},
  MRNUMBER = {2971705},
MRREVIEWER = {Nick Gravin},
       DOI = {10.1016/j.jcta.2012.07.011},
       URL = {https://doi.org/10.1016/j.jcta.2012.07.011},
}



• Improved simulation of nondeterministic Turing machines. (with S. Kalyanasundaram, R. J. Lipton, K. W. Regan)
  • Theoretical Computer Science, Pages 66-73, 2010.
  • abstract | DOI | bibtex

The standard simulation of a nondeterministic Turing machine (NTM) by a deterministic one essentially searches a large bounded-degree graph whose size is exponential in the running time of the NTM. The graph is the natural one defined by the configurations of the NTM. All methods in the literature have required time linear in the size 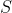of this graph. This paper presents a new simulation method that runs in time . The search savings exploit the one-dimensional nature of Turing machine tapes. In addition, we remove most of the time dependence on nondeterministic choices of states and tape head movements.

@article {MR2885890,
    AUTHOR = {Kalyanasundaram, Subrahmanyam and Lipton, Richard J. and Regan, Kenneth W. and Shokrieh, Farbod},
     TITLE = {Improved simulation of nondeterministic {T}uring machines},
   JOURNAL = {Theoret. Comput. Sci.},
  FJOURNAL = {Theoretical Computer Science},
    VOLUME = {417},
      YEAR = {2012},
     PAGES = {66--73},
      ISSN = {0304-3975},
   MRCLASS = {68Q05},
  MRNUMBER = {2885890},
MRREVIEWER = {B. H. Mayoh},
       DOI = {10.1016/j.tcs.2011.05.018},
       URL = {https://doi.org/j.tcs.2011.05.018},
}



• The monodromy pairing and discrete logarithm on the Jacobian of finite graphs.
  • Journal of Mathematical Cryptology, Volume 4, Issue 1, Pages 43-56, 2010.
  • abstract | DOI | arXiv | bibtex

Every graph has a canonical finite abelian group attached to it. This group has appeared in the literature under a variety of names including the sandpile group, critical group, Jacobian group, and Picard group. The construction of this group closely mirrors the construction of the Jacobian variety of an algebraic curve. Motivated by this analogy, it was recently suggested by Norman Biggs that the critical group of a finite graph is a good candidate for doing discrete logarithm based cryptography. In this paper, we study a bilinear pairing on this group and show how to compute it. Then we use this pairing to find the discrete logarithm efficiently, thus showing that the associated cryptographic schemes are not secure. Our approach resembles the MOV attack on elliptic curves.

@article {MR2660333,
    AUTHOR = {Shokrieh, Farbod},
     TITLE = {The monodromy pairing and discrete logarithm on the {J}acobian of finite graphs},
   JOURNAL = {J. Math. Cryptol.},
  FJOURNAL = {Journal of Mathematical Cryptology},
    VOLUME = {4},
      YEAR = {2010},
    NUMBER = {1},
     PAGES = {43--56},
      ISSN = {1862-2976},
   MRCLASS = {05C50 (14H40 94A60)},
  MRNUMBER = {2660333},
       DOI = {10.1515/JMC.2010.002},
       URL = {https://doi.org/10.1515/JMC.2010.002},
}

Preprints:

• Canonical local heights and Berkovich skeleta. (with Robin de Jong)
  • 29 pages, 2024.
  • abstract | arXiv | bibtex

We discuss canonical local heights on abelian varieties over non-archimedean fields from the point of view of Berkovich analytic spaces. Our main result is a refinement of Néron's classical result relating canonical local heights with intersection multiplicities on the Néron model. We also revisit Tate's explicit formulas for Néron's canonical local heights on elliptic curves. Our results can be viewed as extensions of Tate's formulas to higher dimensions.

@unpublished {arXiv:2405.17826,
    AUTHOR = {de Jong, Robin and Shokrieh, Farbod},
     TITLE = {Canonical local heights and Berkovich skeleta},
      YEAR = {2024},
    EPRINT = {2405.17826},
      NOTE = {Preprint available at \href{https://arxiv.org/abs/2405.17826}{{\tt ar{X}iv:2405.17826}}},
       URL = {https://arxiv.org/abs/2405.17826},
}


Counting two-forests and random cut size via potential theory. (with Harry Richman, Chenxi Wu)
• 20 pages, 2023.
• abstract | arXiv | bibtex

We prove a lower bound on the number of spanning two-forests in a graph, in terms of the number of vertices, edges, and spanning trees. This implies an upper bound on the average cut size of a random two-forest. The main tool is an identity relating the number of spanning trees and two-forests to pairwise effective resistances in a graph. Along the way, we make connections to potential theoretic invariants on metric graphs.

@unpublished {arXiv:2308.03859,
    AUTHOR = {Richman, Harry and Shokrieh, Farbod and Wu, Chenxi},
     TITLE = {Counting two-forests and random cut size via potential theory},
      YEAR = {2023},
    EPRINT = {2308.03859},
      NOTE = {Preprint available at \href{https://arxiv.org/abs/2308.03859}{{\tt ar{X}iv:2308.03859}}},
       URL = {https://arxiv.org/abs/2308.03859},
}

Miscellaneous:

• Oberwolfach report containing the extended abstract of some of my work with Robin de Jong (pages 564-566).



• Notes:

  • Course notes on Abelian Varieties, scribed by various students in class. Here is another version scribed by Dan Collins.
    I have not read or edited either of these notes. I would appreciate any comments or corrections.
  
  
  • Course notes on Non-Archimedean Geometry, scribed by Daniel Miller.
    I have not read or edited the notes. I would appreciate any comments or corrections.
  
  
  • Short note on Basic von Neumann Algebra Theory. It was written mainly for my own benefit.
  
  

• Videos:

  • Video of my talk on Heights and moments of abelian varieties at Zoom Algebraic Geometry (ZAG) Seminar in November 2021.
  
  
  • Video of my collaborator's (Robin de Jong) talk on Asymptotic properties of the Ceresa cycle at Institut Mittag-Leffler in November 2021.
  
  
  • Video of my talk on Graphs and arithmetic geometry at Bay Area Discrete Math Day in April 2021.
  
  
  • Video of my talk on Matroids and their Jacobians at a BIRS/CMO Workshop in November 2015.
  
  
  • Video of my talk on Riemann-Roch theory for graphs and tropical curves at a BIRS Workshop in March 2014.
  
  

---

email: farbod@uw.edu

office phone: (206) 543-1916

office: PDL C-443

---

Disclaimer: This is not a publication of the UW, and UW has not edited or examined the content.

(Last modified on: August 26, 2024)