- Section 2.1: 13-20, 26, 29
- Section 2.2: 1-8, 24, 25
- Section 2.3: 1, 3, 4, 18, 20
- Section 1.1: 15, 16 (suggestion: read p. 7 on "Constructing Mathematical Models")
- Section 2.3: 2, 15, 19
- do more linear and separable equations if you need to
- Section 2.5: 1-5 and 8-13, but use these instructions instead: "determine the critical (equilibrium) points, classify each one as asymptotically stable, unstable, or semistable, and sketch the solution curves."
- Section 2.5: 20-22
- Section 2.5: 7, 18, 26
- this tank problem: A tank contains 50 gallons of solution, which consists of water in which 25 pounds of salt is dissolved. At time t=0, pure water runs into this tank at 2 gallons per minute, and the well-combined mixture flows out at the same rate. There is also a second tank of water, which starts out with 50 gallons of pure water. The outflow from the first tank flows into the second tank, and the mixture flows out at the same rate. When does the second tank contain the greatest amount of salt?
- Section 2.7: 1, 2, 11
- Section 3.4: 1-6, 29
- p. 126: 1-32: identify the type of differential equation (linear, separable, or other; among separable equations, autonomous or not). If linear or separable, solve it. (There are other types of differential equations in that list, types that we don't know how to solve.)
- Section 3.1: 1-16, 20, 22
- Section 3.4: 7-22
- Section 3.1: 21
- A sliding chain: A chain, 5 meters
long, is resting on a table, and 1 meter of the chain is
dangling off the edge of the table. Assume that there is
no friction, so the chain starts sliding off the table.
How much time is required for the chain to slide all the
way off the table?
[Hints: You may assume that the chain has constant density. Also, if you come across an equation like Aebt + C + De-bt=0 and you want to solve it for t, make the substitution u=ebt, multiply the equation by u, and then solve for u. Once you've solved for u, you can get t.]
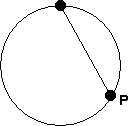
- A sliding bead: Imagine a circle,
positioned vertically. Pick a point P on the
circle different from the top. Connect a wire from the
top of a circle in a straight line to P, and let
a bead slide along that wire. Show that the amount of time
required for the bead to reach the end of the wire doesn't
depend on your choice of the point P.
- Section 3.5: 1-14, 16, 18, 23-30
- Section 3.6: 1-18
- Section 3.5: 38, 39
- Section 3.6: 30, 31
- Section 3.7: 1-10, 13-18
- Section 3.8: 1-4, 6-14, 17, 24
- Section 1.3: 29
- Section 2.4: 32
- Section 3.6: 28
- Gravity problem: Imagine a train which
goes in a straight line through a tunnel between two
points on the surface of the earth (for example, between
Seattle and Rio de Janeiro). Suppose that there is no
friction, and the train just operates under gravity, so if
you start it at one end of the tunnel, at rest, it will
fall into the tunnel, accelerate until it reaches the
midpoint of its trip, decelerate as it nears the other
end, stop at the other end, and then return. Show that
the time required for a complete round trip is the same
for all such tunnels (it doesn't matter whether it ends at
Rio de Janeiro or Beijing or Baltimore), and estimate its
value.
[Hint: inside the earth, the force of gravity is proportional to the distance from the center.]
- Section 3.9: 1-12, 17-19
- Section 6.1: 5, 7-14, 16-20
- Section 6.1: 6, 15, 26, 27
- Section 6.2: 1-23
- Section 6.3: 1-18
- Do these three problems (PDF file).
- Section 6.4: 1-13
- Section 6.5: 1-12