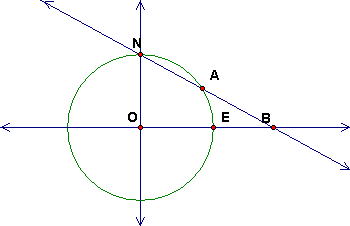
This cross-section shows stereographic projection from the sphere with center O of radius R, with center of projection at N to the equatorial plane perpendicular to the diameter ON.
The point B is the stereographic image of A, a point on the sphere.
Let c be a circle with radius R and center O. Suppose that the inversions of two general points A and B in c are A' and B'. Two (or more) of the triangles that can be formed from the points A, B, A', B' O are similar.
Write a pair of similar triangles.
OAB is similar to OB'A' (one choice - also OAB' is similar to OBA', etc)
Prove the similarity.
By definition of inversion: OA OA" = R2 = OB OB', so OA/OB' = OB/OA'. The angle AOB = angle B'OA, so by SAS the triangles are similar.
State briefly the key idea of how these similar triangles are used to prove that the inversion of a line not through O is a circle (with one point exception)
Let A be foot of perpendicular from O to the line. If B is any other point on the line, angle OAB = right angle = OB'A' by similar triangles. This says all B' are on circle with diameter OA'.
References: Ogilvy and Sved and GTC.
Suppose A, B, and C to be points on the real number line. If A = 1, B = 10, C = 46. For what point D does CD divide AB harmonically?
AC/BC = - AD/BD, so 45/36 = -(d-1)/(d-10) if D = d.
Thus (d-1)/(d-10) = -5/4, so 4d - 4 = -5d + 50 and 9d = 54. Thus d = 6
D = 6
Remark: A basic understanding of harmonic division should tell one that D must be between 1 and 10, so any answer not between these numbers is clearly incorrect. Also, a common error was to get the minus sign wrong and solve AC/BC = AD/CD. When done correctly, clearly the solution is D = C = 46, which should ring some alarm bells.
Question for the class: Why did 2/3 of the class not reduce 45/36 to 5/4? This is still correct but more easily leads to errors.
Define the radical axis of two circles c and d.
Several OK answers, such as:
- Set of points where powers with respect to c and d are equal OR
- Locus of centers of circles orthogonal to c and d.
The radical axis of two circles is a line. Is this part of the definition or not? Yes ____ No _____
No. This is a theorem proved from the definition.
Given triangle ABC and points A' on BC, B' on CA and C' on AB. Suppose the ratio BA'/A'C = 4/3 and ratio CB'/B'A = 5/2.
(a) What are the barycentric coordinates (with respect to ABC) of P, the intersection of AA' and BB'?
If barycentric coordinates are (x, y, z) with respect to ABC, then the ratios on the sides give z/y = 4/3 and x/z = 5/2, thus z = (4/3)y and z = (5/2)z = (10/3)y. If we take y' = 3 (to get integer masses) we get x' = 10, y' = 3, z' = 4. Total mass is 17, so since x+y+z = 1, we divide by 17 to get:
Barycentric coordinates of P = (10/17, 3/17, 4/17)
(b) If AA', BB' and CC' are concurrent, what is AC'/C'B?
AC'/C'B = y/x = 3/10
(c) If A = (1, 1, 0), B = (0, 2, 1), C = (1, 1, 1) what point is P?
P = (1/17)(10A + 3B + 4C) = (1/17)(14, 20, 7)
Let S be the sphere with center (0,0,0) and radius 1. The plane p with equation x+y+z = 1 intersects S in a circle c.
The circle c is a circle in the plane p, but it can also be considered as a spherical circle of points whose spherical distance from a center on the sphere is constant.
(a) What is the center C of this circle c in the plane p?
C = (1/3)(1, 1, 1). Note that (1/3) + (1/3) + (1/3) =1 so this point is on the plane.
(b) What is the radius of c in plane p?
Distance |OC|2 = 1/3, so if the radius of the circle is r, by Pythagoras
r2+ |OC|2 =1, so r = sqrt(2/3)
Radius = sqrt(2/3)
(c) What is a center D of this circle on the sphere S?
D = (1/sqrt(3))(1, 1, 1)
(d) What is a spherical radius of this circle? (angle measure or given as an inverse trig function)
The spherical radius is the angle opposite r in the right triangle with hypotenuse 1 and legs r = sqrt (2/3) , |OC| = sqrt(1/3) , so the spherical radius = arcsin r = arcsin sqrt (2/3)
Another way to answer this is with dot product. The spherical distance is the angle between the center D and a point such as (1, 0, 0) on the circle, so the cos of the angle is the dot product = 1/sqrt 3. So the angle = arccos sqrt(1/3). Same angle.
Spherical radius = arcsin sqrt (2/3) = arccos sqrt(1/3).
(a) Given point K = (0,0,1) and point P = (a, b, c), write the parametric formula for line KP. Choose the parameter t so that t = 0 at K and t = 1 at P.
Parameterization: (1-t)K + tP = (0,0,1) + t(a, b, c-1)
(b) Use the parameterization above to write a formula in terms of (a, b, c) for the intersection Q of the line KP and the plane with equation z = 0.
Set 1 + t(c-1) = 0 to get t = 1/(1-c).
Q = (a/(1-c), b/(1-c), 0)
|
This cross-section shows stereographic projection from the sphere with center O of radius R, with center of projection at N to the equatorial plane perpendicular to the diameter ON. The point B is the stereographic image of A, a point on the sphere. |
|
· If A is 45 degrees from N in spherical distance, calculate the distance from O to B.
Think of OE as x-axis and ON as y-axis. Coordinates of A are Rsqrt(1/2)(1, 1).
IF OB = x, similar right triangles give x/R = (x-Rsqrt(1/2))/Rsqrt(1/2)
so (sqrt(1/2) - 1)x = -Rsqrt(1/2).
Thus x = CR, where C = sqrt(1/2)/(1 - sqrt(1/2)).
C can also be written in other ways by simplifying the denominator, for example
C = 1/(sqrt (2) - 1) = (1+sqrt(2))/(2-1) = 1+sqrt 2
Distance (in terms of R) = R(1+sqrt 2) (or other formulations above)
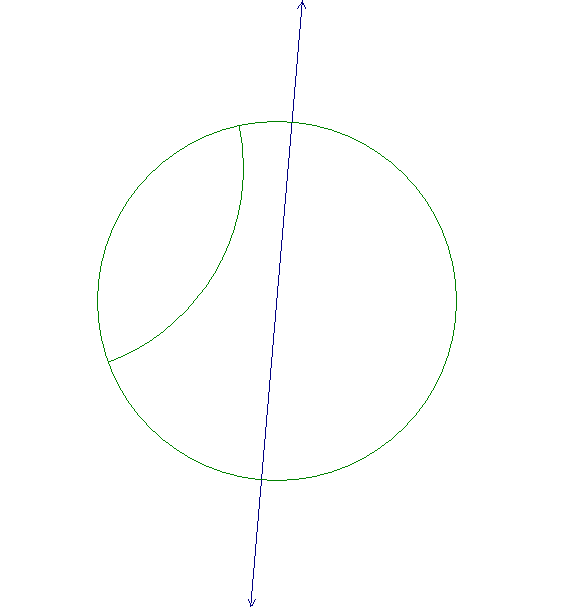
This figure shows two P-lines in the Poincaré disk model (one of the P-lines is a Euclidean segment). Construct the P-line m orthogonal to both of these lines.
Solution: Draw line through endpoints of the arc. Intersect this line with the given line to construct M, the center of the support of m. Then construct tangent segment MT, from M to the given circle. (Either do this by constructing the center of the P-disk as the midpoint of the given segment or you could use the polar construction with a straightedge.)
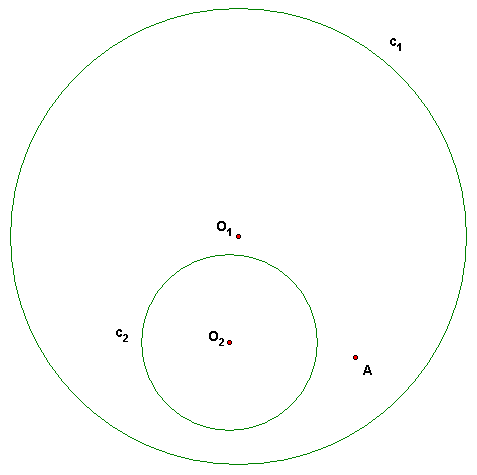
Write briefly and clearly your main steps. O1 and O2 are the centers of c1 and c2.
(a) Construct and label the circle m through A and orthogonal to c1 and c2.
Invert A in c1 and c2 and construct m as the circumcircle of A and the two inversion points.
(b) Construct and label the circle d through A that is in the same coaxal family (pencil) as c1 and c2.
The center of d is on line O1O2. It is also on the tangent line to d at A. Intersect these two lines to find the center D of d. The construct the circle through A.
(c) Construct and label a point N so that for a circle n with center N, the inversion images of c1 and c2 are concentric circles. (Just construct N. Do not invert!)
N is either of the intersection points X and Y of m with line O1O2. Then if we invert with center X and the circle through Y, the circles in the elliptic pencil turn into lines through Y and the circles in the hyperbolic pencil, c1, c2, d, turn into concentric circles with center Y. See Ogilvy or Sved or GTC.
For answer follow this perspective link.
|
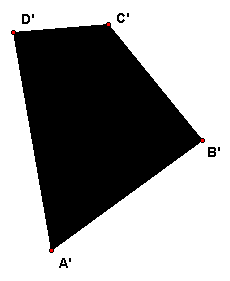
The figure on the right is made of 4 squares. The figure below shows a central projection (or perspective drawing) A'B'C'D' of the square ABCD. · Construct the rest of the projected figure. In other words construct points E', F', G', H', I' so that the new figure is a central projection of the one above to another plane. Write a few words, enough to make clear what you did. You do not need to justify your construction so long as it is clear. |
|
Problem |
Points |
|
1 |
25 |
|
2 |
15 |
|
3 |
15 |
|
4 |
25 |
|
5 |
25 |
|
6 |
20 |
|
7 |
15 |
|
8 |
15 |
|
9 |
25 |
|
10 |
20 |
|
Total |
200 |