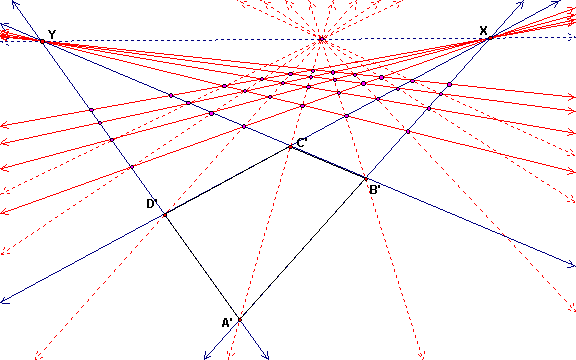
Drawing a Square Tiling in Perspective

Suppose we want to draw this figure of squares in perspective. In other words we want to draw the central projection of this figure onto another plane.

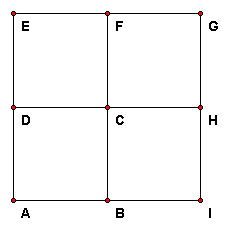
If we are given this image of ABCD, is there enough information to figure out the rest of the figure, with the images of the points EFGHI?

The answer is Yes. In fact there are ways to do this with an unmarked straightedge, as well as a way using inversion and harmonic division. The straightedge secret is to figure out some lines in the original figure that intersect in the labeled points and then pick the line whose images we know how to draw in the perspective drawing.

Unmarked Straightedge Solution #1

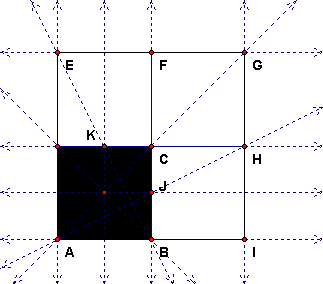
Step 1. One approach is to construct the midpoints of the sides of the square by intersecting the diagonals and constructing parallels. Here are some lines in the original figure, all of whose images we can draw in the projection.

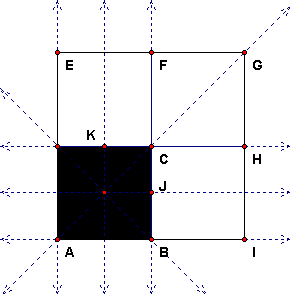
Now the images of the parallel lines AB and CD intersect at a point X and the images of AD and BC intersect at a point Y. Then the line XY is the horizon line. We construct O' as the intersection of the diagonals and then construct the image of the line through O parallel to AB as the line O'X. Likewise O'Y is the image of the line through O parallel to AD. Then intersections give J' and K'.

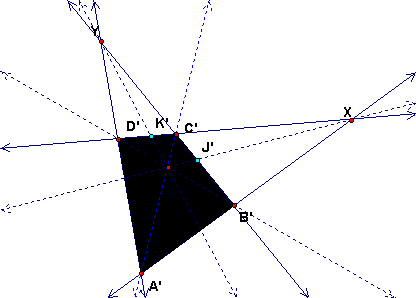
Step 2. Next we observe that line AJ intersects line CD in point H and line BK intersects line AD in point E. This gives two of the needed points. But then the line through H parallel to AD intersects line AB in point I and the line through E parallel to AB intersects line BC in point F. Finally, line HI intersects line EF in G. The images of all these lines can be drawn in the perspective drawing.

Note: There are a number of other choices to get needed points. For example, DJ intersects AB in I, etc.

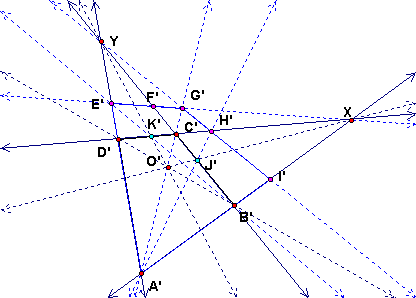
Specifically, in the projection, get H' as the intersection of A'J' and C'D' and E' as the intersection of B'K' and A'D'. Then draw line EX and line HY as the images of the parallels to AB and AD, respectively. Intersect the appropriate lines to get I', F' and G'.

Unmarked Straightedge Solution #2

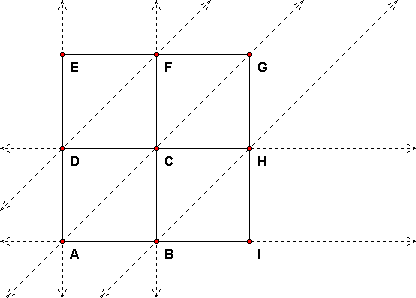
This method uses the diagonals the horizon systematically to give an even quicker solution. Draw the extended sides of ABCD and also construct the parallels through B and D parallel to AC. Then these parallels intersect sides CD and BC in H and F.

The points H' and F' can be constructed from the images of these lines. Let Y be the intersection of A'C' and XY. This is where the image of line AC meets the horizon. Thus the images of the other two parallel lines are B'Z and D'Z. Then H' and F' can be defined as intersections as shown.

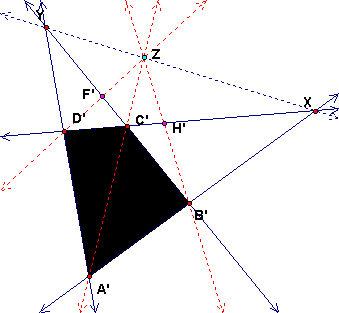
The rest of the points can be constructed by drawing the images of the other lines parallel to sides of ABCD. Draw F'X and H'Y and intersect with the lines shown to get the rest of the image points.

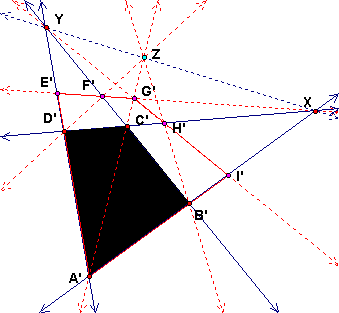
Solutions 3 & 4: Harmonic sets and/or Inversion

Another way to approach the construction of the projection image is to think of harmonic sets. B is the midpoint of AI. If we let X* be the point at infinity on AB, then the points B and X* divide AI harmonically. By the definition of harmonic division, we have seen that this also means that AI divides BX* harmonically. But harmonic sets are preserved by central projection. Since X is the image of X* then A'I' divides B'X harmonically. We are given A', B', X so we can construct I' by one of the constructions of a harmonic set.

The ruler construction from the complete quadrangle would be to choose points P and Q so that A' is on line PQ. Then A' is one of the 3 diagonal points of the quadrangle B'XPQ. The other two are the point U = intersection of PX and QB' and V = PB' and QX. Then I' is the intersection of UV with line A'B'.

But we have done this above with P = C' and Q = Z. In this case U = G' and V = Y.

Any construction of I' so that A'I' B'X is harmonic will do. For example, an option that uses a compass would be to invert A' in the circle with diameter B'X.

In any event, this construction of I' can be repeated to construct E' on A'D' and then lines E'X and I'Y can be intersected with other lines to give the rest of the points.

More Tiles

Using the diagonal line idea from Method #2, it is possible to draw lines through Z and then after intersecting to get new points, draw lines through these points and X and Y to get new images of parallels to the sides of ABCD. In this way, one can draw the perspective image of a whole floor with as many square tiles as desired. Notice that along any line such as A'B', this also gives a way of marking the perspective images of evenly spaced points on a number line. This is useful for drawing fences, buildings, etc;, and for measuring distance in the original figure from the perspective drawing.