Inequalities in Triangles

Vertical Angles

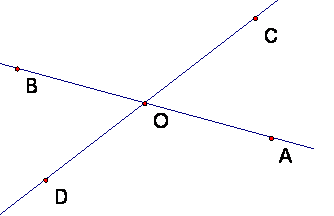
Definition: Angles AOC and angle BOD are a pair of vertical angles if rays OA and OB are opposite rays of the line AB and if rays OC and OD are opposite rays of line CD. 

In other words, the two segments AB and CD intersect at O.  When two lines intersect at a point O in this way, they form two pairs of vertical angles, AOC and BOD and BOC and AOD, as in the figure.

Theorem:  If AOC and BOD are a pair of vertical angle, they are congruent.

Proof:  This follows from observing that AOC and COB are supplementary (i.e, their sum is a straight angle), and also that COB and BOD are supplementary. See B&B, p. 52.

Exterior Angle Theorem

Definition of an exterior angle of a triangle

In triangle ABC, the interior angle at A (normally called just angle A), is the angle BAC. 

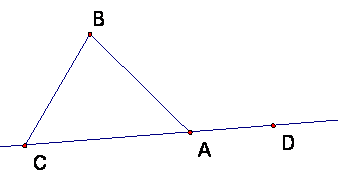
If D is any point on the opposite ray of AC, then DAB is an exterior angle of the triangle ABC at A.  (There is a second exterior angle at A formed by extending side AB instead of side AC, the two exterior angles are a pair of vertical angles.)

Theorem:  An exterior angle at A of triangle ABC is great than either of the (interior) angles B or C.

Proof:  For the proof, construct this figure.  M is the midpoint of AB and ME = CM (so M is also the midpoint of CE).

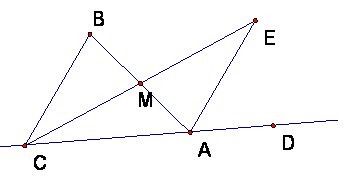
Then triangle MBC = triangle MAE by SAS, because

• angle CMB = angle EMA, by vertical angles
• MB = MA , since M is the midpoint of AB
• CM = EM, since M is the midpoint of CE

Consequently, by corresponding angles, angle MBC = angle MAE.

But angle MBC = angle B in the triangle.

Angle MAE < angle MAD, because E is in the interior of angle MAD (discuss).

Greater Angle and Greater Side in a Triangle

Theorem:  In a triangle ABC, side BC is greater than side CA, if and only if angle A (= angle CAB) is greater than angle B (= angle ABC).

In other words, greater sides are opposite greater angles.

Proof.

Part 1. First we prove one direction: greater sides imply greater opposite angles

Since BC > CA, then there is a point D on segment BC so that CD = CA.

• But this means triangle CAD is isosceles, so angle CAD = angle CDA.
• But angle CAD < angle CAB, since D is between C and B.
• And angle CDA is an exterior angle at D of triangle ABD, so angle CDA > angle ABC.
• Together, this says angle CAB > angle CAD = angle CDA > angle ABC.

Part 2.  Now we assume angle A is greater than angle B and prove that BC > CA.

This is accomplished by a bit of logical pigeonholing using Part 1.

If A is greater than B, we have three cases as possibilities

1. BC < CA
2. BC = CA
3. BC > CA

Case 1, by Part 1 above, implies that angle B < angle A, which contradicts the hypothesis.

Case 2 would imply that triangle ABC is isosceles with angle A = angle B, which again contradicts the hypothesis.

So Case 3 is the only possible case that can occur, and this proves Part 2.

QED

Triangle Inequality

This extremely important inquality is stated and proved at this link.