Theorem: In a triangle, the length of any side is less than the sum of the other two sides.
So in a triangle ABC, |AC| < |AB| + |BC|. (Also, |AB| < |AC| + |CB|; |BC| < |BA| + |AC|.)

This is an important theorem, for it says in effect that the shortest path between two points is the straight line segment path. This is because going from A to C by way of B is longer than going directly to C along a line segment.
Proof:
We will add something to the figure that “straightens out” the broken path. Construct point D on line AB so that BD = BC and so |AD| = |AB| + |BC|.
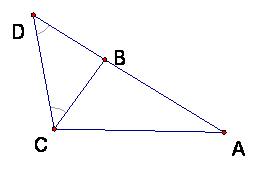
Then since triangle BDC is isosceles by construction of D, then the base angles DCB and CDB are congruent. But angle DCB is smaller than angle DCA; for this angle is contained inside angle DCA, since B is between D and A.
But this means that in the triangle ADC, Angle D is less than angle C, so for the opposite sides: |AC| < |AD|. But |AD| = |AB| + |BC| by the ruler axiom.
QED
Theorem: If A, B, C are distinct points in the plane, then |CA| = |AB| + |BC| if and only if the 3 points are collinear and B is between A and C (i.e., B is on segment AC).
Proof:
First we prove that the equality is true if B is between A and C. Choose a ruler on the line AB; then the 3 points correspond to numbers a, b, c and either a < b < c or c < b < a.
Suppose a < b < c. Then |AC| = |c – a| = c – a = (c – b) + (b – a) = |c – b| + |b – a| = |AB| + |BC|. This uses (carefully) the order of the numbers, so that |c – a| = c – a, because a < c, for example. The case c > b > a gives the same result.
For the other direction, the converse, we must prove that if |AC| = |AB| + |BC|, then the points are collinear and B is between A and C.
First, the points must be collinear, for if they were not, then ABC would be a triangle and the triangle inequality would be true. If the points are collinear, then as we saw from the ruler computation, B must be between A and C. If this were not the case, and if, say A were between B and C, then |CB| would = |CA| + |AB|. But we would still have |CA| = |AB| + |BC|, so together these would give |CB| = |AB| + |BC| + |AB|, or 0 = 2|AB|. This is impossible for distinct points A and B.
QED
So in the end if A, B, C are distinct points on the plane, and |AC| is greater than or equal to each of |AB| and |BC|, then there are 2 possible cases and one impossible case.
|AC| < |AB| + |BC| (ABC is a triangle)
|AC| = |AB| + |BC|, (B is on segment AC)
|AC| > |AB| + |BC| (impossible)
Or in other words, for distinct points A, B, C, it is always true that |AC| is less than or equal to |AB| + |BC|, with equality occurring precisely when B is on segment AC.
Corollary: For any 4 non-collinear points A, B, C, D, the distance |AD| < |AB| + |BC| + |CD|.
Proof:
Either ABD is a triangle or ACD is a triangle (or both) because of non-collinearity. Suppose ABD is a triangle. Then |AD| < |AB| + |BD|. Next get |BD| < or = |BC| + |CD| from BCD.
QED
Note: This can be extended to any number of points using the same idea.