Math 487 Lab 9B
|
What to turn in from Part B?
Lab 9 -- you can do it with Sketchpad or by drawing
and construction on paper
For each experiment there is a pattern to create that
should be saved (Sketchpad) and turned in on paper. Turn in a printout
or drawing on paper, whatever tool you use.
Also, answer a few questions.
The instructions for what to turn in are found in
the blue boxes at the end of the experiments.
|
Part B consists of generating a series of patterns of squares with a
triangle inside.
These patterns can be created with Sketchpad or on graph paper. If you use
graph paper, you can the triangular design or you can cut out a cardboard template.
Wallpaper symmetric patterns over the whole
plane
The first part of this exercise will be to create
some examples of repeating symmetric patterns from an original square "tile".
The second part will be an analysis of the symmetries of each pattern.
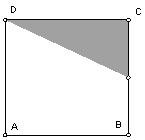
Constructing the Tile
This will be our basic tile. Construct the figure
by constructing a square ABCD and shading in the triangle with vertices at C,
D and the midpoint of BC.
If you are using Sketchpad:
- Make more copies of the page with
this figure in your document from File > Document Options > Add Page
> Duplicate Page 1.Save this sketch.
You will use it as the basis of several experiments.
If you are using graph paper:
- Draw this tile in a square of the graph paper. You will want to make the
square of a size that you can form an 8x8 pattern of squares.
Experiment 4: Pattern 0. Translations
Sketchpad: Start with a fresh page with the square figure above.
Select A and B (not the segment) and Mark AB as vector. Then translate the whole
figure by AB (you may want to leave out the segment AD and points A and D from
this to avoid duplication).
Graph Paper: One can translate the square pattern by moving the pattern
to the next square as described above, and drawing there.
- Then translate the new figure again and again
until you have a row of 8 squares.
- Now mark segment BC as vector and translate
the row of 8 squares by BC to get a new row.
- Translate the new row by BC
also and continue until you have 8x8 squares with the triangular pattern inside
each. You may want to resize ABCD by dragging A or B if the pattern is too
large for the screen.
Analysis of Pattern 0
Assume the pattern is continued "to infinity".
- What are the vectors that define translation symmetries
of this pattern?
- What are the centers of rotational or point symmetry?
What are the mirror lines of line symmetry?
- Are there glide reflections that are symmetries?
From Experiment 4: Pattern 0 -- To turn in
- The figure from this experiment.
- Answers to these questions
Questions
- If continued to infinity, does this pattern have any rotations,
reflections or line reflections as symmetries?
- What are the symmetries of this figure?
|
Experiment 5: Pattern 1. All sides as mirrors
Start with a new page with the same single square with the triangle
inside.
Sketchpad:
- Now mark segment AB as mirror and reflect the whole
figure.
- Now mark segment BC as mirror and reflect the whole figure in BC.
- Then reflect the whole figure across CD. Then reflect
the whole figure across DA.
- Continue reflecting until you have 8x8 squares. You
may want to resize ABCD.
Graph paper: With a square cardboard template, one can reflect over
an edge by flipping the square over along the edge. With this change, follow
the instructions above.
Analysis of Pattern 1
Assume the pattern is continued "to infinity".
- What are the centers of rotational or point symmetry?
- What are the vectors that define translation symmetries
of this pattern?
- What are the mirror lines of line symmetry?
- Are there glide reflections that are symmetries? What are the invariant
lines of glide reflection symmetry?
From Experiment 5: Pattern 1 -- To turn in
- The figure from this experiment.
- Draw in symbols for the symmetries of this pattern -- double or
thick lines for reflections, dashed lines for invariant lines of glide
reflections, little squares for centers of 90-degree rotation, little
rhombi for centers of point reflection
|
Experiment 6: Pattern 2. Two corners at
centers of rotation.
Start with a new page with the same single square with the triangle
inside.
Sketchpad:
- Mark A as center and rotate the whole figure by 90 degrees.
- Rotate the original shape by A90 two more times. (Why would more
times add nothing to the pattern?)
- Now mark B as center and rotate the whole figure by 90 degrees. (Note:
if you look carefully, it is often the case that you can get the same resulting
figure by selecting and rotating only a piece of the whole.)
- Then rotate everything by B90 two more times.
- Then rotate everything by A90 3 times.
- Continue until the figure contains an 8x8 square of
square patterns and nothing new emerges in the 8x8 pattern
- You may want to resize ABCD.
Graph paper: It is possible to figure out rotations of the pattern using the
graph paper as a visualization tool. Be sure to use the same points A and B
as centers for the whole exercise. Don't move the centers with the squares.
Analysis of Pattern 2
Assume the pattern is continued "to infinity".
- What are the centers of 90-degree rotational symmetry?
- What are the centers of point symmetry that are not
also centers of 90-degree rotational symmetry?
- What are the vectors that define translation symmetries
of this pattern?
- What are the mirror lines of line symmetry?
- Are there glide reflections that are symmetries? What are the invariant
lines of glide reflection symmetry?
From Experiment 6: Pattern 2 -- To turn in
- The figure from this experiment.
- Draw in symbols for the symmetries of this pattern -- double or
thick lines for reflections, dashed lines for invariant lines of glide
reflections, little squares for centers of 90-degree rotation, little
rhombi for centers of point reflection
|
Experiment 7: Pattern 3. A corner rotation
and a mirror
Start with a new page with the same single square with the triangle
inside.
Sketchpad:
- Now mark A as center and rotate the whole figure by
90 degrees 3 times.
- Now mark segment BC as mirror and reflect the whole figure in BC.
- Rotate the while figure by A90 again 3 times.
- Then reflect the whole resulting figure in BC.
- Continue rotating and reflecting until the figure contains
an 8x8 squre of square patterns and nothing new emerges in the 8x8 pattern
by continued rotation or reflection.
- You may want to resize ABCD.
Graph paper: Again, one can carry out the rotations and reflections
on graph paper.
Analysis of Pattern 3
Assume the pattern is continued "to infinity".
- What are the centers of 90-degree rotational symmetry?
- What are the centers of point symmetry that are not
also centers of 90-degree rotational symmetry?
- What are the vectors that define translation symmetries
of this pattern?
- What are the mirror lines of line symmetry?
- Are there glide reflections that are symmetries? What are the invariant
lines of glide reflection symmetry?
From Experiment 7: Pattern 3 -- To turn in
- The figure from this experiment.
- Draw in symbols for the symmetries of this pattern -- double or
thick lines for reflections, dashed lines for invariant lines of glide
reflections, little squares for centers of 90-degree rotation, little
rhombi for centers of point reflection
|
More Patterns from the Square -- for later
There are more ways to fill the plane with this
square pattern, though some may turn out to be the same old ones in disguise.
Here are some other ways.
- Generate the pattern using point reflection (rotation by 180 degrees),
placing centers at each of the midpoints of the sides of ABCD.
- Make one transformation be rotation by 90 degrees with center A and
the second be rotation by 180 degrees with center B.
- Define a glide reflection with vector AB and mirror (invariant) line
= perpendicular bisector of AD. As a second isometry, add translation by AD
or else a glide reflection in the vertical direction.
Link to Lab 9 Part A

