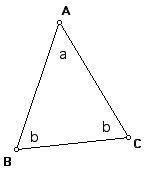
Given a triangle ABC with AB = AC, the angles opposite the equal sides are equal. Let a = angle BAC and let b = angle ABC = angle ACB. Using the angle sum theorem, if a is known, then b is determined, and if b is given, then a is determined. Write down the relationship between a and b. If b is known, solve for a: a = If a is known, solve for b: b =

Angles in Convex Polygons

Study the two figures of the convex quadrilateral ABCD and the convex pentagon ABCDE divided into triangles.

• Tell what is the sum of the vertex angles of ABCD. Will this work fot any convex quadrilateral? Explain.
• Tell what is the sum of the vertex angles of ABCDE. Will this work fot any convex pentagon? Explain.
• Generalize this to a formula for the sum of the vertex angles of any convex polygon with n sides.

Complications with Nonconvex Polygons

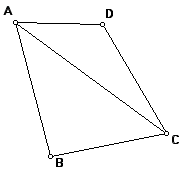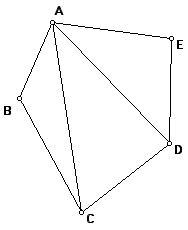Study the two figures of the nonconvex quadrilateral ABCD and the nonconvex pentagon ABCDE divided into triangles.

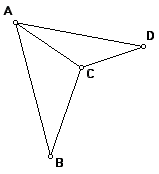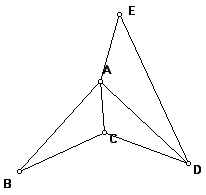What goes wrong in ABCD if you choose diagonal BD?

What is the measure of angle C in ABCD (approximately)? If your answer is less than 180 degrees, does the angle sum formula work? If your answer is greater than 180 degrees, how can you tell in general which angle to measure, the big one or the little one?

It is possible to sort out nonconvex polygons and get a nice relationship, but we will do this later with some new ideas.

Regular Polygons

Definition: A convex polygon is a regular polygon if all its angles are congruent and all its sides are congruent.

1. If a triangle has all angles congruent, must it be regular? Explain.
2. If a quadrilateral has all angles congruent, must it be regular? Explain.
3. If a quadrilateral has all sides congruent, must it be regular? Explain.
4. What is the common name for a regular quadrilateral.

If this definition is combined with what we know about angle sum, it is possible to deduce the measure of the vertex angles of any regular polygon.

1. For a regular triangle, what is the angle measure of one of the vertex angles?
2. For a regular quadrilateral, what is the angle measure of one of the vertex angles?
3. For a regular pentagon, what is the angle measure of one of the vertex angles?
4. For a regular hexagon, what is the angle measure of one of the vertex angles?