Angles in the Regular Pentagon

Angles and Ratios in Regular Pentagons

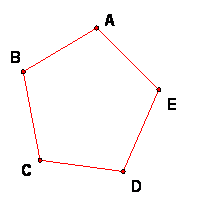
Angles in the Regular Pentagon

What is the angle at any vertex of a regular pentagon?

Pentagon with 2 Diagonals

This pentagon is divided into 3 triangles. Compute the measure of all the angles in the figure.

Pentagon with All Diagonals

This pentagon is shown with all its diagonals. Compute the angle measure of all angles in the figure and label the equal angles clearly in the figure.

Parallelograms and Rhombi in the Pentagon

In the figure, shade in or thicken the outline of a rhombus.

How can you be sure that this is a parallelogram?

How can you be sure that this is a rhombus?

Write down the 4 equal sides of your figure.

Similar isosceles triangle

Find triangles with these qualities, using the labeled points in the figure above.

Two Obtuse Isosceles Triangles: Write down (using the letters for the vertices, such as triangle XYZ), the names of two similar obtuse isosceles triangles that are not congruent. What are the angles of these triangles?

Three Acute Isosceles Triangles: Write down for the vertices, the names of 3 similar acute isosceles triangles, no two of which are congruent. What are the angles of these triangles?

Ratios in Regular Pentagons

Look in the figure of the pentagon with diagonals above. Find a figure like this in which all 3 triangles (the big one and the two sub-triangles are isosceles. LABEL the triangle with the letters that correspond to your discovery in the pentagon. JUSTIFY why you can say the 3 triangles are isosceles. What equalities of lengths must be true?

MAJOR PROBLEM: Let the side of a regular pentagon be s and the length of a diagonal be d, use this figure to find the ratio d/s. (Hint: Is it legit to set s = 1 to simplify?)