Fourier analysis and sequence waveforms

In this project, we use the phrase periodic sequence to refer to a sequence that gives rise to a periodic waveform. Such sequences are those sequences A={a_n} with the property that there exists a P such that n is in A if and only iff n+P is in A. One class of such sequences are those of the form a_n = mn, where m is a positive integer (for example, if m=4, then the sequence begins 4, 8, 12, 16, 20, ...). The waveform for such a sequence can be analysed with fourier methods (see here). The waveform will have fundamental frequency 44100/m hz, and the spectrogram will exhibit spectral lines at every integer multiple of 44100/m.

For example, this is the spectrogram for the waveform made with m=11, showing the fundamental at 44100/11=4009.09... hz, and the four harmonics below 22050 hz.

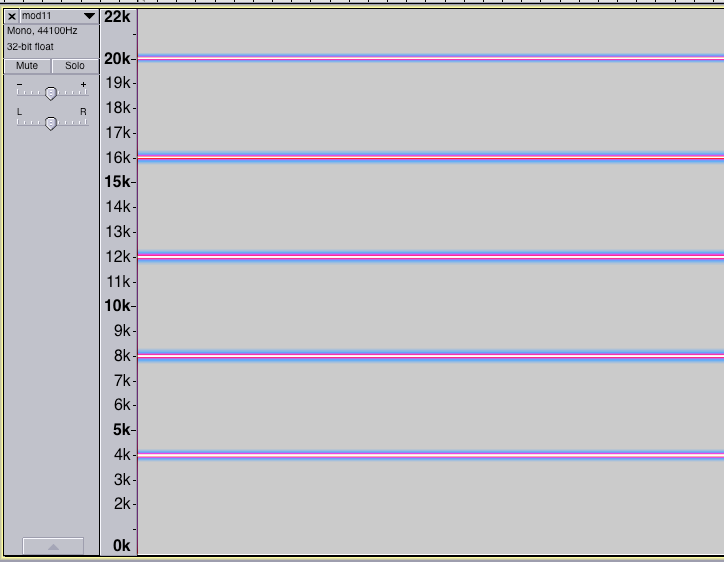
In practice, only multiples of the fundamental less than 44100/2 = 22050 need to be considered: the waveform generated with this subset of harmonis will be audibly indistinguishable from the actual waveform.