WXML Autumn 2019
Number Theory and Noise
Jingyun Du, Pubo Huang, Jin Lin, Sam Wang
This project investigates the representations of sets of positive integers (sequences) as sound.
A digital audio waveform is created from a given set A of positive integers by setting sample number i to a non-zero constant c for all i in the set. All other samples are set to zero.
For example, the waveform for the primes starts like this:
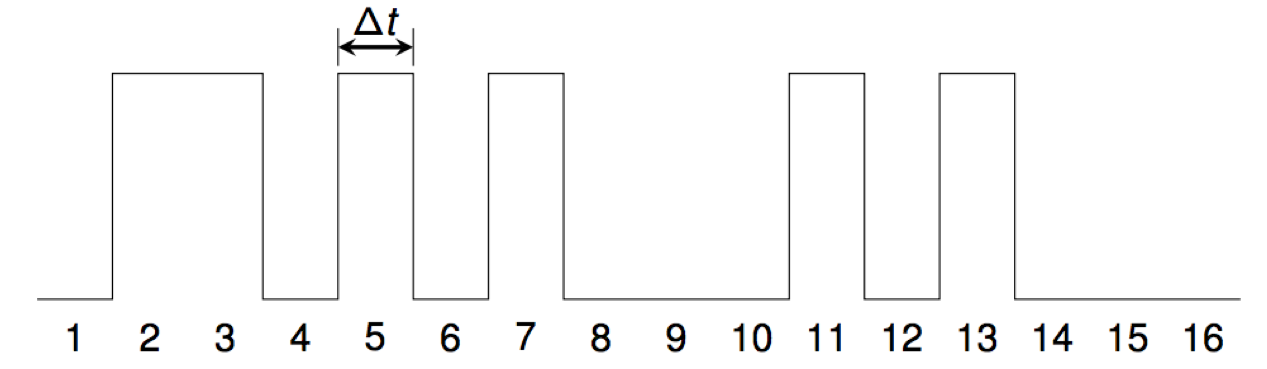
We use the standard CD-audio sampling rate of 44100 samples per second, so Δt = 1/44100= 0.0000226757... seconds.
For many sets, the result is what most people would describe as noise.
OEIS sequences
| OIES id | description | sound player | download | creator | quarter | tags | comments |
|---|---|---|---|---|---|---|---|
| A008846 | Hypotenuses of primitive Pythagorean triangles | download | Jin Lin | Aut2019 | |||
| A000788 | Total number of 1's in binary expansions of 0, ..., n. | download | Jin Lin | Aut2019 | digits | ||
| A054632 | Partial sums of the sequence of digits of the natural numbers: 1,2,3,..,9,1,0,1,1,1,2,1,3,1,4,... | download | Jin Lin | Aut2019 | digits | ||
| A067112 | Partial sums of the sequence of digits of the primes (2,3,5,7,1,1,1,3,...) | download | Jin Lin | Aut2019 | digits | ||
| A067113 | Partial sums of the sequence of digits of the squares (1,4,9,1,6,2,5,...) | download | Jin Lin | Aut2019 | digits | ||
| Partial sums of the sequence of digits of n^3 | download | Jin Lin | Aut2019 | digits | |||
| Partial sums of the sequence of digits of n^4 | download | Jin Lin | Aut2019 | digits | |||
| Partial sums of the sequence of digits of n^5 | download | Jin Lin | Aut2019 | digits | |||
| Partial sums of the sequence of digits of n^n | download | Jin Lin | Aut2019 | digits | |||
| Partial sums of digits in decimal expansion of 2^sqrt(2) | download | Jin Lin | Aut2019 | digits | |||
| A099539 | Partial sums of the digits in decimal expansion of sqrt(2) | download | Jin Lin | Aut2019 | digits | ||
| A099534 | Partial sums of the digits in decimal expansion of e | download | Jin Lin | Aut2019 | digits | ||
| Partial sums of the digits in decimal expansion of sqrt(3) | download | Jin Lin | Aut2019 | digits | |||
| A067113 | Partial sums of the sequence of digits of the squares (1,4,9,1,6,2,5,...) | download | Jin Lin | Aut2019 | digits | ||
| A225771 | Numbers that are positive integer divisors of 1 + 2*x^2 where x is a positive integer | download | Jin Lin | Aut2019 | |||
| A000408 | Numbers that are the sum of three nonzero squares. | download | Jin Lin | Aut2019 | |||
| A000404 | Numbers that are the sum of 2 nonzero squares. | download | Jin Lin | Aut2019 | |||
| A000379 | Numbers n where total number of 1-bits in the exponents of their prime factorization is even; a 2-way classification of integers: | download | Jin Lin | Aut2019 | |||
| A000328 | Number of points of norm <= n^2 in square lattice. | download | Jin Lin | Aut2019 | |||
| A164620 | Primes p such that 1 +p*floor(p/2) is also prime. | download | Pubo Huang | Aut2019 | primes | ||
| A164624 | Primes p such that p+floor(p/2)+floor(p/3) is prime. | download | Pubo Huang | Aut2019 | primes | comment | |
| A164625 | Primes p such that p+floor(p/2)+floor(p/3)+floor(p/5) is prime. | download | Pubo Huang | Aut2019 | primes | ||
| A000960 | Flavius Josephus's sieve numbers. | download | Pubo Huang | Aut2019 | |||
| A046959 | Numbers n where sin(n) increases monotonically to 1. | download | Pubo Huang | Aut2019 | |||
| A093083 | Partial sums of digits of decimal expansion of golden ratio, phi. | download | Pubo Huang | Aut2019 | digits | ||
| Partial sums of digits of randomly-generated decimal expansion. | download | Pubo Huang | Aut2019 | digits | |||
| Numbers n for which the digit sum of n^2 is 28 | download | Pubo Huang | Aut2019 | digits | |||
| Numbers n for which the digit sum of n^2 is 31 | download | Pubo Huang | Aut2019 | digits | |||
| Numbers n for which the digit sum of n^2 is 72 | download | Pubo Huang | Aut2019 | digits | |||
| A259368 | Number of binary digits of n^n. | download | Pubo Huang | Aut2019 | digits | ||
| floor( n atan(n/10^3)) | download | Pubo Huang | Aut2019 | ||||
| floor( n atan(n/10^4)) | download | Pubo Huang | Aut2019 | ||||
| floor( n atan(n/10^5)) | download | Pubo Huang | Aut2019 | strictly increasing portion of floor( n atan(n/10^6)) | download | Aut2019 | |
| A000430 | Primes and squares of primes. | download | Sam Wang | Aut2019 | |||
| A000452 | The greedy sequence of integers which avoids 3-term geometric progressions. | download | Sam Wang | Aut2019 | |||
| A000469 | 1 together with products of 2 or more distinct primes. | download | Sam Wang | Aut2019 | |||
| A000549 | Numbers that are the sum of 2 squares but not sum of 3 nonzero squares. | download | Sam Wang | Aut2019 | |||
| A000966 | n! never ends in this many 0's. | download | Sam Wang | Aut2019 | |||
| A001043 | Numbers that are the sum of 2 successive primes. | download | Sam Wang | Aut2019 | |||
| A001101 | Moran numbers: n such that (n / sum of digits of n) is prime. | download | Sam Wang | Aut2019 | |||
| A001122 | Primes with primitive root 2. | download | Sam Wang | Aut2019 | |||
| A001123 | Primes with 3 as smallest primitive root. | download | Sam Wang | Aut2019 | |||
| A007624 | Product of proper divisors of n = n^k, k>1. | download | Sam Wang | Aut2019 | |||
| A007634 | Numbers n such that n^2 + n + 41 is composite. | download | Sam Wang | Aut2019 | |||
| A007638 | Numbers k such that 3*k^2 - 3*k + 23 is composite. | download | Sam Wang | Aut2019 | |||
| A007692 | Numbers that are the sum of 2 nonzero squares in 2 or more ways. | download | Sam Wang | Aut2019 | |||
| A007774 | Numbers that are divisible by exactly 2 different primes. | download | Sam Wang | Aut2019 | |||
| A003277 | Cyclic numbers: n such that n and phi(n) are relatively prime; | download | Sam Wang | Aut2019 | |||
| A003159 | Numbers n whose binary representation ends in an even number of zeros. | download | Sam Wang | Aut2019 | |||
| A002035 | Numbers that contain primes to odd powers only. | download | Sam Wang | Aut2019 | primes | ||
| A001958 | floor( (n+1/3) * (5+sqrt(13)) /2) | download | Sam Wang | Aut2019 | |||
| A001958 approximation: difference sequence is 5, 4, 4, 4, 5, 4, 4, 5, 4, 4, then repeats. | download | Sam Wang | Aut2019 | ||||
| A001969 | Evil numbers: numbers with an even number of 1's in their binary expansion. | download | Jingyun Du | Aut2019 | |||
| A027699 | Evil primes: primes with even number of 1's in their binary expansion. | download | Jingyun Du | Aut2019 | |||
| A125494 | Composite evil numbers. | download | Jingyun Du | Aut2019 | |||
| A014574 | Average of twin prime pairs. | download | Jingyun Du | Aut2019 | |||
| A045718 | Nearest neighbors of primes. | download | Jingyun Du | Aut2019 | |||
| A088485 | Numbers n such that n^2 + n - 1 and n^2 + n + 1 are twin primes. | download | Jingyun Du | Aut2019 | |||
| A111980 | Union of pairs of consecutive primes p, q with q-p = 4. | download | Jingyun Du | Aut2019 |