
This article is one of a matched pair in French and English resulting
from a three-way collaboration between Guy Brousseau, Nadine Brousseau
and Virginia Warfield. It was launched by the desire of the latter
to make available to the English-speaking community an article
written by Guy Brousseau in 1981. The resulting discussions produced
so many modifications and clarifications that the three undertook
to make the improved version available also in French. The process
provided splendid evidence that differences in linguistic and
cultural perspective can be a source of considerable intellectual
enrichment.
One of the most widely known articles in the "gray literature"
of the field of Didactique is the "Cas de Gaël"
(the Case of Gaël), by Guy Brousseau, which originally appeared
in 1981. It is the Cas de Gaël which, modified, clarified
and translated, is the main content of the current article. In
order to explain its importance, we will start with the background
of the article, and of its author.
Guy Brousseau began his career in the classroom, teaching, experimenting,
observing and writing reams of notes. He then spent the decade
of the Sixties simultaneously extending his knowledge of mathematics
and using the knowledge he had gained in the classroom as a basis
for interpreting the works of Diènes, Piaget and others
(or possibly vice versa). This heady combination produced, in
1970, the Theory of Situations, which was to generate the entire
field of Didactique des Mathématiques. A brief description
of the theory appears in the general introduction below.
But it was not a theory intended to be merely decorative. Brousseau
was determined to see it tested and expanded by means of serious
experimentation. To that end, he threw himself into an effort
being made by a group of mathematicians in and around Bordeaux,
as part of a general movement led by A. Lichnérowicz to
persuade the Ministry of Education to provide the means to modernize
the teaching of mathematics. These means consisted of I.R.E.M.'s
(Institutes for Research in Mathematics Education), at which university
professors and in-service teachers could carry out research combining
their respective fields of expertise. Their labors paid off,
and the I.R.E.M. of Bordeaux was duly founded-one of the first
such in France. Brousseau joined it, with the task of arranging
for the carrying out of his projets.
For that, Brousseau further persuaded the university and ministry
to set up the Ecole Michelet, which combines the properties of
being a regular public elementary school and of being designed
for controlled, observed experimentation in the teaching of mathematics.
During the same period, Brousseau carried out a study on the
learning processes of a number of students in "selective"
mathematical difficulty-that is, students who in other academic
areas were at a reasonable level, but who were for some reason
failing in their mathematics. The specific situation of the study
is described below, but it seems worthwhile to point out one of
the many ways in which this case resonates with more familiar
contexts. In the course of my first reading of the original article,
I was haunted by a feeling that I had met up with Gaël in
some other circumstance, under some other name. Eventually it
dawned on me that he could have stepped right off the pages of
John Holt's "Why Children Fail". He influences his
instructor with exactly the sweet submissiveness Ruth.
In her case, though, whether consciously or unconsciously, she
leads the tutor into reducing the content of the problem practically
to nothing. This is, in fact, the method of Gaël's friend
Cyrille, but his manner of accomplishing it is more that of Emily,
whose inability to sustain uncertainty turns her into what Holt
calls an "answer-grabber". Gaël and Cyrille may
have been small, French schoolboys, but they represent an international
legion!
Gaël, aged 8 1/2, was one of nine children in selective
(mathematical) difficulties whom I tried to help by a small number
of clinical, didactical tutorial sessions between 1976 and 1983.
I prepared the sessions, recorded them, transcribed them and
analyzed them with my friend Jacques Pérèz, a psychologist,
and a small team of collaborators and students. The subjects
of the studies were
They attracted attention to two forms of avoidance of learning
in a school situation: Gaël's "hysteroid" form
and the more frequent and more visible obsessional form.
These studies were carried out in parallel with other research,
all of it directed towards developing and testing the Theory of
Situations which was in the process of being elaborated. The Theory
of Situations is based on the idea that human knowledge is manifested
in its rôle in the interactions between systems: actors,
milieu and institutions.
The theory of situations is based on the idea that human knowledge
manifests itself in the interactions between certain systems:
subjects, milieus and institutions. To each piece of knowledge
it should be possible to associate a limited number of specific
types of interaction whose proper development requires that knowledge,
or even causes it to develop. The characteristic situations for
pieces of mathematical knowledge can be studied ane even modeled
within the framework of mathematics itself, which sometimes makes
it possible to use computation to predict their evolution.
The teaching of a notion consists thus of setting up its situations
and carrying out interactions in which the learner can take part.
It is, itself, an interaction. We have shown that this interaction
is also largely specific to the knowledge being taught but that
it takes a form-a didactical situation-necessarily different from
the non-didactical forms in which knowledge is used. This result
changes the entire approach to mathematics education and the education
of teachers.
The theoretical and experimental study of didactical situations
and their practical consequences is a long story in which le
Cas de Gaël has held an important place. There are three
major reasons for this importance:
1.1 The session itself. Red Cars
The tutor launches the first session with the question: "Do
you know what things you had trouble with this week and what things
you really knew how to do?" He gets only evasive replies.
Gaël takes out his notebook and the two examine the week's
work. They eventually choose the following problem, which Gaël
had done wrong:
In a parking lot there are 57 cars. 24 of the cars are red.
Find the number of cars in the parking lot which are not red.
Gaël thinks a moment, then announces: "I am going to
do what I learned from the teacher." He writes 57 + 24
in a column and gets 81- exactly what he had done during the week.
It appears that Gaël has mastered the operation of addition,
which he has to carry out frequently, but he never once asks himself
when it is supposed to be used. Instead, he covers himself with
the authority of the teacher to justify an automatic use of the
operation. He pays no attention whatever to the corrections made
in class.
The tutor comments, without too much emphasis, as if it were general remark, that you need to know when to do addition or subtraction or something else; then, in an encouraging tone, he suggests that Gaël draw the cars "but not all of them, because that would take too much time."
Gaël draws a rectangle and writes 57 in the middle.
T: (the tutor) asks: "Is that all of the cars?"
G: " It's all of the cars that aren't red."
T: "Only the cars that aren't red?"
G: "It's all of the cars and they aren't red."
The tutor could have continued with "Then where are the
red cars?", but it was obvious that the child did not have
a correct representation of the situation. Putting him into a
formal contradiction would serve only to embarrass him.
T: "If the number of cars changed, that might change the operation?"
G: "Yes!!"
It is clear that what Gaël calls "operation" is
the triple of numbers, not "addition" as opposed to
"subtraction". The tutor had hoped that Gaël might
have in mind the question: add or subtract? In that case, he would
have tried to find out if the child was able to construct an equivalent
problem using small numbers for which the drawing could have been
done quickly. The fact that Gale doesn't understand the question
obviates the possibility of pursuing this line. The tutor asks
Gaël to draw the 57 cars, one by one. Gaël starts off
trying hard to make pictures that really look like cars, but at
the instigation of the tutor, switches to making marks. The tutor
has him make them in lines of twenty.
.T: " Have you drawn all of the cars in the parking lot?"
G: "No"
T: "The directions were 'In a parking lot there are 57 cars. Draw the parking lot.' Are there 57 cars in this parking lot?"
G: "Yes"
T: "Are all the cars the problem was talking about in this parking lot?"
G: "No, there are some red cars, too."
The tutor points out that he needs to pay careful attention to
the text, because there is a period after the "57 cars".
Gaël then admits that the red cars are in the lot, but thinks
he still needs to draw them because they don't show up in his
design.
Here one can see that he has difficulty in envisaging that
there is only one set of cars, with two properties:
being in the parking lot and being red. For him, the second property
necessitates a second set, and even though he admits that the
second set also has the first property, he can't yet conceive
of its being a part of the original set. Is it because he hasn't
analyzed the statement of the problem, or because he can't use
the operation of inclusion?
The tutor explains that the 24 red ones are part of "these"
cards-the original 57-and Gaël should paint them red on his
design. At this stage, Gaël's actions are totally guided
by the tutor. Together they verify that the drawing corresponds
to the problem statement, then Gaël has to find all of the
cars which are not red. He counts 31 of them. The tutor asks:
T: "If I tell you it's the wrong answer, do you think I am right?"
G: "I don't know."
T: "What would you do to find out if I am right?"
G: "I'd count again."
And he gets 33.
T: "So, which is right, 31 or 33? What can we do to find out?"
G: "We have to count."
T: "There's no other method?"
No answer.
His drawing having been sufficiently concrete and having made
it possible for him to give an answer, Gaël doesn't try to
use, or think of using, an operation to verify his answer, because
he can count as often as he likes. His drawing is a sure support
to which he can refer, whereas an operation calls for certain
abstract mechanisms and includes a reversibility which Gaël
seems not to have acquired, to know how to use subtraction to
find the two terms of the addition.
Gaël does another recount: "33".
The tutor circles the red cars,

gets Gaël to observe that there are thus 24 red and 33 non-red
and asks:
T: "So how many cars are there?"
G " I do 24 and then 33?"
Gaël sets up an addition problem: 24 + 33 = 57
T: "So have you got the answer they were calling for? Can you answer the question the problem asked?"
G: "No"
For most children, the answer required is supposed to be the
result of an operation, and the solution is to be found at a specific
spot in the arrangement of what was written. This habit is an
obstacle when it comes to identifying the answer in an equation
regarded as a relation.
T: "Yes you can! You wrote what they asked you to write."
G is astonished. At the request of the tutor he rereads the problem.
T: "How many cars are there that are not red?"
With the aid of the drawing, he gets Gaël to say that there
are only 33. He asks him how he found them and Gaël answers
"by calculating", then corrects it to "by drawing."
The tutor explains that calculating "is so we can find the
answer without having to draw everything" and Gaël
acknowledges that that is what he doesn't know how to do.
The tutor decides to get Gaël to use the symbolic representation
in use in his classroom, with the idea that it will help him.
Gaël draws the parking area, puts in the red cars, then
the others, and then attaches labels:
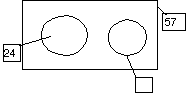
T: "If I count the red ones I get...?"
G: ""24"
T: "And if I go on and count the rest I get...?"
G: "57"
The tutor writes 24
+...
57
set up so that Gaël will not use subtraction to find 33 and
instead will try to find the number which can be added to 24 to
get 57, which he does easily.
In the course of this first phase certain characteristics begin
to appear which are common among students in difficulties: difficulty
in making sense of the question asked and in working out strategies
to check the answer; recourse to recipes, etc.
To clarify the nature of Gaël's difficulties and to insure
that he will not once again draw a set of automatic conclusions
from this sequence, the tutor poses two similar problems.
The first has the cars forming two disjoint sets clearly identified
in the statement of the problem. All that is needed is to add
their numbers to get the total, which Gaël does swiftly.
The other one is comparable to the initial problem, with 8 cars of which 3 are red. Gaël draws a circle with 8 cars
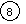
then does the drawing over to include the 3 reds :
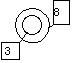
and when asked how many are not red he replies "11".
Once again he applies to the authority of the operation he knows,
without stopping to think. By drawing the cars and coloring three,
as before, he does get the answer.
It should be explained that in Gaël's class subtraction
had not been introduced as the only way to find a difference.
Addition with a gap was frequently used. This procedure tends
to force the child out of the automatic formal association of
a mathematical operation with a material operation (+ if I add,
- if I take away) and to transfer the focus to the set which is
being counted and its relationship with the givens of the problem.
1.2 Test of the quantification of inclusion
The incomprehension Gaël demonstrated in this exercise could
simply have had psychogenetic origins: the child might be too
young to carry out the necessary reasoning. Solving a problem
like this, which involves considering the whole and the part simultaneously
so as to compare them, assumes a type of logical operation which
Piaget showed to have a complex character. The quantification
of inclusion required for the understanding of the car problem
is, in fact, not constructed by a child until around the age of
seven or eight. It was therefore necessary to assure ourselves
that Gaël had an operational scheme. We decided on the spot
to give him the colored balls test. This well-known test, used
by Piaget in the work cited above, consists of presenting the
child with eight wooden beads, of which five are red and three
green. The subject has to judge whether there are more wooden
beads or red beads and to justify his answer. Gaël succeeded
with the test , justifying us in our thinking that the repeated
failures of the child in the use of the relation of inclusions
did not result from gaps in access to logico-mathematical structures.
1.3 Test of commutativity
We then decided to present Gaël with another operational
test used by Gréco in his research on the genesis of the
operation of commutativity.
The child is presented with a set of rods set up as follows:
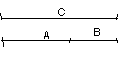
It is clear to the child that A + B = C
Rod B is then put in place of rod A and the child is asked to make a mark where the end of A would come to if A were put after B:
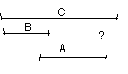
Gaël says immediately : "The end is going to be right where it was before!" and makes a mark in line with the end of C
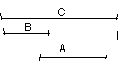
The response characterizes a child who has achieved the operational
stage, which does not surprise us as all, given the age of the
child and his success with the preceding test. What is, on the
other hand, interesting, and can provide us with some information,
is the attitude of Gaël when we cast some doubt on his judgment
by objections along the lines of "but a kid told me a few
minutes ago that the end is short of that", etc. Gaël
instantly backs off of his assertions:
G: "That might be right..."
T: "What do you think, exactly?"
G: "I don't know!"
This type of conduct on this test characterizes children whom
Gréco situates in an intermediate (pre-operational) stage,
where the structures of the subject are still under construction,
so that the compensations are incomplete and fragile. This cannot
be the case with Gaël. It would seem that without any doubt,
his sudden absence of conviction in the face of a simple counter-proposition
has to do with his general attitude towards others around him
when his own knowledge is put into play. The conviction which,
for Piaget, reveals the functioning of an operational structure
disappears here without its being possible to blame it on a fragility
of logical constructions. It is the result, we think, rather
of his manner of being with those around him.
1.4 Analysis of the first session
Among the questions arising from Gaël's behavior there was one which had to be checked out swiftly. All mathematical activity is supported by operational schemes of the subject which, according to Piaget, are not learned in the strict sense, but constructed in the course of development. In the case of the red and non-red cars, we could see that it was absolutely necessary to assure ourselves that Gaël really did have the operational structure of inclusion.
With the results from the test with the wooden beads, we know
at least that Gaël's repeated failures to understand the
problem could not be explained by gaps at the level of his logico-mathematical
structures. Manifestly, he had the operational schemes necessary
to solve the problem proposed. How then to explain his behavior
in the course of the session?
The response is guaranteed not to be simple from the moment that
one takes as an object the relationship between a single
subject whose current relationship with the world is the result
of a lot of past history and a didactical situation which itself
is quite complex.
In this perspective, Gréco's test gives us something to
start with. The immediate cause for surprise is Gaël's complete
incapacity to maintain his conviction in the face of anyone else's
contradiction. One counter-proposition is enough to produce doubt
right when to all appearances he was feeling completely convinced.
A characteristic of the child thus appeared which we had already
encountered in the course of a psychological examination on a
more general front: flight from any possible confrontation and
the avoidance of conflict at any cost by taking refuge in a position
of dependence and submission.
It seemed to us that this might well have an impact on Gaël's relationship with mathematical knowledge. In the area of knowledge, there is, in effect, an attitude where dependence offers the non-negligible benefit of a security: knowledge is always somebody else's knowledge which one has only to appropriate; thus, one eliminates the risk of having oneself put into question in a debate about truth. There is no need to offer any reason for what one takes for truth other than the invocation of the authority to whom one refers. (Gaël says "what I was taught", "what the teacher says I have to do")
But the price of this attitude is an incapacity to conceive of
a process of construction where knowledge might be the result
of a confrontation with reality, and in which the subject becomes
the author of his own knowledge. Mathematical knowledge thus risks
being simply a ritualized activity of reproducing models.
Situations of the type that students normally encounter in class
tend to present certain closed characteristics. For example,
the teacher poses a question and all of the students are
supposed to find the answer-the same one-so that the minute
one student publicly produces the answer, all of the others stop
looking for it. Furthermore, it is the teacher who pronounces
the solution correct so that each student has only one
chance per problem to attempt to find the solution. This way,
every one of these situations functions as a test and learning
has to happen elsewhere-from the correction and the explanations
that accompany it, for example-by means other than trying things
out and observing the effects of one's own decisions. Eventually,
and partly in consequence, the solution frequently can't be envisaged
unless the child already has a representation of the situation
which permits him to bring out the cognitive objects in question,
the more so since the verification of the validity of the answer
and the explanations of the teacher call on this same representation,
on the already achieved knowledge which produced the answer.
Otherwise stated, this learning situation gives no opportunity
to make or attempt a decision-thus to learn-except to those who
already know most of it. In these situations, the student can
only acquire the right representation of the situation by making
the connection between similar tests by a convenient sort of reinforcement
by association.
Situations of this type are not helpful it all in getting students
like Gaël to modify their relationship with either the givens
of the problem or objects of knowledge.
To augment and enrich a student's relationship with the situation,
one classic procedure consists of asking them to represent-to
draw-the elements that are involved. That is what was done in
this session, and it showed that making the correct drawing required
exactly the representation that the student lacked. It seems reasonably
clear that although this schematization may perhaps produce progress
in an existing representation, it cannot create one.
On the contrary, the repetition of problem-situations which the
teacher expects to be the key to comprehension tends to put the
student in a situation of slightly anxious, passive waiting, where
the activities have a ritual and almost magical character. This
reaction is visible all through the first session: " I am
going to do what the teacher taught me..."; when he adds
he recites carefully "I put this here, I carry this,...the
tens column..." and marks off each step. His representations
are more or less analogues of reality, and he tries to draw things
that really look like cars. But the fact that he stays very close
to the concrete, far from producing the required meaning for the
operation, seems to be taken by the child as a means of keeping
his distance from any reasoning about the objects.
When the tutor asks him: "Have you drawn the red ones?"
he answers "No, only the black ones", and it is true
that he hasn't drawn the red ones (in red). He focuses on his
drawing without making it play the role of a representation for
checking on the information in the problem statement. And when
he is asked to color over the marks representing red cars with
a red crayon he forgets how many there were and the tutor has
to stop him at 25. In general, numbers are of very secondary importance
to him. He says 50 and he counts 31, then 33, he forgets...he
acknowledges his errors with good grace-and detachment.
A classical approach in dealing with children in difficulty consists of identifying the errors or mistakes that they make, and if they are repeated, interpreting them as anomalies in the development of the child, or gaps in their acquisitions which need to be remedied because "they are going to make the child unable to progress in mathematics."
For example, we observed that Gaël frequently wrote 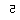 for 5, or wrote 12 for 21 which could be interpreted as a lack
of spatial structure or even trouble with spatio-temporal
perception. In the same way, Gaël's difficulties in connecting
his drawing with the text of the problem could be classified as
malfunctionings of the symbolic function.
for 5, or wrote 12 for 21 which could be interpreted as a lack
of spatial structure or even trouble with spatio-temporal
perception. In the same way, Gaël's difficulties in connecting
his drawing with the text of the problem could be classified as
malfunctionings of the symbolic function.
This classical analysis leads to a search for remedies in the
form of exercises "of the same type" in the sense of
these functions: exercises in spatial structure, etc. This is
the opposite of the teacher's search, which is for exercises "of
the same type" in the sense of the same mathematical subject
treated from the same didactical point of view: writing numbers,
dictation of numbers, subtraction problems, etc. In this sense,
the first appears therapeutic relative to the second, The approach
we are trying here is very different: it's a matter of working
at the level of the learning situations and manipulating their
characteristics so as to obtain the desired changes in attitude.
For that we will use a "theory of situations" which
we discuss elsewhere. This theory studies, as its principal object,
the conditions of the milieu which make the behavior of the subjects
and the manifestation of knowledge necessary and plausible..
Gaël's relationship with knowledge-at least the knowledge
involved in the classroom-is strictly superficial. His habit
of avoiding problems and keeping his distance lead to stereotypical
actions of a purely "didactical" nature-that is, centered
entirely on the relationship with the teacher without mobilizing
any of the assimilation schemes which, for all that, he does have
at his disposition. Gaël accommodates himself to a set of
institutionalized relations which on his side call forth only
rituals which do not engage him at all. It seems possible, thus,
that all of Gaël's attitude during this first session is
the consequence of an accord between the habitual didactical situation
in the class as he perceives it and his defensive relationship
with knowledge of which we spoke earlier.
One cannot maintain the position that the didactical situation
that Gaël habitually encounters is the sole cause of his
failures in mathematics. If it were, why would other children,
no better armed than he on the cognitive front, succeed? All we
can think is that he finds this situation a convenient one in
that it lets him escape the effort of constructing knowledge.
And he can escape it all the better for his manner of dealing
with adults-his own particular social attitude made up of sweetness
and submission, which defuses all criticism, leaving him forearmed
against any form of conflict with the teacher.
Why does this cause failure? Because, if the habitual didactical
situations permit learning in the closed conditions we described
above, it is because the debate on knowledge is replaced by another
type of debate-one which deals with the learning student. Learning
badly, not knowing, making thus and such an error are all forms
of running afoul of the will of the teacher, of being in conflict
with him. From there out, the student can only escape conflict
and all the resulting difficulties by building something which
will take the place of knowledge and of learning.
Now Gaël, we would say, escapes this debate in the extent
that he disarms all conflict by a total absence of aggressiveness.
In student-centered debate, the conflict effectively feeds on
itself: the teacher's aggressiveness calls for a habitual response
of agressiveness from the student, which in turn feeds the aggressiveness
of the teacher, etc., with the subject having no way out except
by producing the expected results. Gaël, for his part, doesn't
join this game. His profoundly submissive attitude disarms all
hostility ("He's always ready to acknowledge his mistakes
and he's really sorry" says the teacher.)
1.5 Projects for the next session
The set of analyses we have been able to make leads us to envisage
how we are going to handle the second session. The essential
issue will be to introduce a rupture in Gaël's conceptions
of a didactical situation by offering him a situation which will
require of him anticipation, prediction and the undertaking of
responsibility, that is, that he invest (in the sense of an army
of occupation) the object of knowledge. To do that, we are going
to stay on the same mathematical subject and propose to him what
we call a situation of action.
Only if it becomes apparent that Gaël cannot enter into
this type of relationship with knowledge will we search for other
means of intervening.
1.6 Commentary: Topaze and the recalcitrant student
In order to make a certain number of didactical concepts available,
we are going to start with a commentary-possibly a slightly heavy-handed
one-on a famous example of a teaching situation: the first scene
of Marcel Pagnol's play, "Topaze".
[Translator's note: in order to avoid jeopardizing Brousseau's
excellent commentary, we have chosen to translate the passage
word for word. The reader is therefore in dire need of the following
information: in French the words for lamb ("mouton")
and lambs ("moutons") are pronounced identically, as
are the words for was ("était") and were (étaient")]
" Some lambs...some lambs...were safe in a park...in a park." [He leans over the shoulder of the Student and starts again] Some lambs...some lambsss...[the student looks up, startled] "See here, my friend, make an effort. I'm saying lambsss. Were" [he repeats with great finesse] "we-re. That means there was not just one lamb. There were several lambsss."
In this ironic and touching scene, Pagnol brings out with almost
cruel relevance several common characteristics of this kind of
situation.
The teacher wants to obtain a certain behavior from his student-here the correct spelling, under dictation, of the word "lambs". This behavior signifies that the student has correctly interpreted a situation-in this case, the sentence-that he has recognized a problem, at least implicitly-does lambs have an s or not?-and that he has resolved it by the application of a piece of knowledge, possibly a practical one-in this case, the rule for pluralizing nouns.
In this case, the student doesn't solve the spelling problem
which has been set him, and Topaze can't bring himself to accept
the situation. The problem is that the expected behavior provides
not just a piece of information about the state of the student,
but also the material on which the rest of the teacher's activities
are based. The mistakes in the text produced are too numerous
and too trivial, which makes it impossible to base any reasonable
"lesson" on it. For the teacher, this subordinate error
in accord needs to be eliminated right away. But he can't resolve
himself either to give the student the correct answer flat out
or to put on explicit pressure (for example by giving a warning
like "Pay attention!") He therefore transforms the spelling
test into a mini-situation of learning. And what does he do? He
tries to obtain the same behavior but by changing the problem.
His second reading completely changes the situation-a student
conscious of the dilemma: "singular or plural?" would
have found the answer by solving a simple phonetics problem.
Obviously, his behavior would then have had neither the same meaning
nor the same value.
Alas, the student doesn't take up this new game. He emphasizes
by his startled air that he doesn't understand why his teacher
is expressing himself in such an extravagant manner. And Topaze
is constrained to explain his poor ruse and justify himself: "One
lamb...several lambsss". He simultaneously provides the
open choice between the possibilities-i.e., the contents of a
lesson undoubtedly reproduced a hundred times-and the solution
in the current case. The student finally registers the problem
and its solution at the same time. He has contented himself with
identifying what the teacher wants through the transparent veil
of a didactical disguise.
We can see thus how Topaze proposes a sequence of situations
all attempting to produce the same behavior, but giving it completely
different meanings, which are progressively less and less rich,
and cost the student less and less of an investment and of knowledge.
It's a kind of negotiation: Topaze tries to obtain the student's
behavior "at the best price" , that is, with the situation
which will have the most meaning for the student, and everything
shows that the student is content to wait until Topaze proposes
the contract which will require the least effort of him.
In these conditions, of what could the hoped-for learning consist?
The teacher ends up choosing a situation which enables the student's
system of knowledge to furnish the desired response. The correct
behavior can be produced by the repertoire which he has already
acquired, but which has nothing to do with the new knowledge that
was the goal. The hope that learning will happen with this strategy
is based on the belief that repetition of relevant questions associated
with answers which are correct but obtained with inadequate knowledge
will cause the correct knowledge to arise. This is impossible
even if the scale of the decreasingly difficult questions being
posed to the student until he furnishes the right answer is graduated
and frequently repeated. Between an inadequate repertoire and
an adequate repertoire there is a leap consisting of exactly the
knowledge to be acquired.
2.1 Session and observations
The tutor presents Gaël with the goal of the session: it's to teach him the things he didn't know how to do the last time, which a child his age should be able to do and which he, too, will soon know how to do. But this teaching will take the form of a game.
This prologue has no impact whatever. Apparently the word "game"
is frequently used to introduce simple exercises.
The materials consist of circles and triangles, large and small. The tutor has Gaël count the number of pieces, of which there are 52, and tells him to write the number on a sheet of paper. Afterwards, for assurance that there really are 52 pieces, the tutor recounts , pointing out that he is using stacks of ten: a pile of 26 triangles, then a stack of 10 circles (=36) then another (=46) then a stack of 6 circles: total 52 pieces.
Once the pieces are counted, they are put in a bag and the bag is closed, and the game consists of remembering what was in the bag.
The tutor asks the child if he knows what there was, to which he replies: "triangles", then hesitates and adds: "squares" (there were none)... "circles". Then at the request of the tutor he draws

"We counted how many pieces?" asks the tutor.
"26"
"26?"
"No, 52"
"What did I count 26 of?"
Gaël no longer remembers. He thinks a long time, but has to be reminded that it was triangles.
Next the tutor explains that they are going to play a guessing
game:
"What do you think I am going to ask you?"
"How many circles there are."
"Do you remember how many there were?"
"No"
"Then we can look in the bag if you don't know. But before
we take them out and look at them, we have to make a bet. Do you
know what that means?"
Gaël says he sometimes bets a franc against his father that
he will be the first to reach the bottom of the swimming pool.
The game, then, consists of betting how many circles there are
and writing down the number. Then if the verification confirms
that number, the bet is won.
First bet: Gaël states that there are 10 circles.
Verification: There are 26. Gaël smiles and agrees with
the tutor that he has lost his bet.
Starting with this first round, and this will be confirmed
in the following rounds, it is noticeable that the number 10 plays
a special role for Gaël. He has registered the fact that
the tutor arranged the pieces in stacks of 10, and this might
perhaps have contributed to his first choice, but as we will see
further on, this is not the only reason.
The tutor proposes that henceforth the bet will be for a caramel.
Gaël smiles.
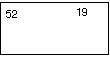
After this first failure, they decide to start again. But Gaël has already forgotten the goal of the session and doesn't remember any more what they counted first and believes that it was just the circles. The tutor therefore has him write again the number of pieces-52. Then he has him count the large red circles: 19. He verifies the latter by again making a stack of 10 and a stack of 9, then they put everything in the bag and close it.
Gaël writes on his sheet of paper:
"What do we need to do?", the tutor asks.
"Find out how many triangles there are."
"Yes . And were there any squares?"
"No. Just triangles and circles."
When the child said the first time that there were squares,
he was probably speaking at random, not having inspected the
different pieces, busy as he was with counting, and having trouble
backing off enough to think about what he was counting.)
In any case, this first scene confirms Gaël's difficulty
keeping track of the givens, and even of the task at hand.
This time, the task is going to be to find out how many are not "big circles", that is, the number of little circles and triangles taken at the same time.
Gaël thinks a bit: "Triangles...there were lots of
them" and makes a random guess of 50.
He writes 52 19 50
The tutor gets him to confirm that it's a matter of counting triangles and little circles and draws underneath the numbers the things that according to Gaël they represent:
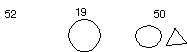
He then sums the situation up by saying that there are 50 on one
side and if the big circles are added there will be 52, then asks
if he wants to stick with his bet. Gaël takes it back, because
he observes that to get from 50 to 52 there wouldn't be many big
circles, "there are just 2".
He corrects his choice and announces 30, then writes
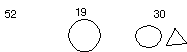
To verify, he takes the objects out of the bag, counts that there
are 33 and exclaims: "I was really close!"
It is important to remark that he is still really at the level
of trial and error, and each time he is trying his luck, but
little by little efforts at reasoning are beginning to appear.
Here, certainly, the tutor, cashing in on favorable circumstances,
introduced a fundamental method of verifying the values being
guessed and thus provoked a contradiction between what the child
predicted and what he observed and a first step in taking charge
of the situation. There was a risk that this departure from a
state of encouraging neutrality would throw Gaël back into
his dependence on the adult and back to looking for his answers
in the adult's questions. But this observation was made in the
form of a summary of what Gaël had just said and done-a summary
which the adult addressed to himself, without even asking any
questions. The observation was so clear to the child that he
didn't spot any intention directed toward him. The tutor took
care to accept the next proposal without comment.
"That's better", says the tutor, "but you still
haven't won. Shall we play again?"
Gaël accepts-one can tell that he would really like to win.
Again he writes 52, counts the small circles (7) puts all
of the pieces in the bag and is supposed to guess the number of
things that are not small circles. .
He thinks out loud: "There are 52...since there are 7 small
circles...". He laughs because he is trying to add 7 to something
to get 52 and he has a feeling he is on the right track. He writes
42 (note that that is 52 - 10) and makes the bet. But first he
verifies by using his fingers to add 42 + 7, observes his mistake,
crosses out 42, writes 49 (the number most recently arrived at-42
+ 7) . He can go no further and he makes the bet.
All the counters are taken out of the bag, the tutor has him
stack them in tens, and there are 45 (which are not small circles).
Gaël crosses out 49 and puts 45, which gives 52 7 42
49 45
The tutor remarks: "There's a trick-but it has to be found."
For the first time, the tutor indicates that the results to be
expected are determined by the givens.
The number of givens that Gaël pays attention to has suddenly
increased a lot, and he can only handle the cycle once through:
choice, anticipatory verification, rejection, new choice. The
bet is a period when the tension relaxes-a pleasant moment of
pretending to think, hesitating a little, then deciding and solemnly
shaking hands with the tutor. Then with a bit of slightly feverish
excitement the sack is opened, the count is reckoned, the resulting
number is compared with the prediction, while the tutor looks
on dubiously with furrowed brow, simultaneously sorry, encouraging
and comically powerless. The bets have to remain reasonably dense
to maintain the child's pleasure-they are the real source of gratification.
The fourth bet again has a prize of a (hypothetical) caramel bar. This time the little triangles are counted (13) but then put into another bag, into which the bag with the other pieces is also put.
As before, Gaël mutters to himself as he calculates: "52
there, 13 there". He counts on his fingers, slows down at
10, then picks back up again and says "42". But after
a long re-count he corrects it to "41"
To verify, the tutor empties the first bag-that is, his dumps
the 13 triangles on the table and puts the other bag to the side,
closed.
"If you have won", he says "there will be 41 in there [pointing to the other bag] and counting all of them there will be...?"
"52"
Starting with 41, Gaël then counts the 13 little triangles:
"42, 43, ..." and gets 54.
Since the bag hasn't been opened, he still has the right to change
his bet, and the tutor lets him search.
Gaël was forgetting the method of verification (or possibly
he was trying to count backwards, which requires simultaneously
counting what is being taken away and the result: 1 - 51, 2
- 50, 3 - 49, -but that's improbable.)
The tutor opportunely again suggested the method of verification
and helped him to get it working, but Gaël didn't take this
as a new set of directions, because he could think of the method
as already agreed on, and his principal problem, at that moment,
was to count correctly and to have a strategy for choosing the
numbers to try.
Gaël smiles, seems to remember something and counts on his
fingers from 13 to 52.
But in the course of doing so, he stops because he has lost track
of how many he has counted so far, and tries another method:
"Oh! There are 13 there. I take away 10 and that leaves 3 and in the other one there are ...45...there are 52. I take away 10, that leaves 40...5. 45!" (42 + 3, maybe?)
"Let's verify!" Again the number turns out to be wrong
and the tutor suggests trying another number. He chooses 40, adds
13 (by counting all of the triangles one by one) and seeing himself
so close to the goal he exclaims: "Aha! I have a proof already!"
but which one?
Next he tries 31, The tutor writes all of the numbers which
do not work, and beside them the result of adding 13, giving successively:
41 54
40 53
31 44
43 56
33 46
42 55
34 47
Now the method of verification is really working. The fact of
being able to count the objects in the known part has differentiated
the functions of the three numbers: the solution number -the one
that is being bet on, and from which the count starts-the number
of objects in the known part which are to be counted (rather than
added), and the total number of objects which is the final number
the count should get to. It is doubtful that this algorithm has
been acquired as a general solution for subtraction problems,
but it will be useful in exploring relations invariant under translation
and from there it will permit an approach to a method of solution
and of sorting out several problems in numeration and the primary
structure of the natural numbers. Above all, it permits an investment
of the terms of the relationship that is to be understood.
Let us observe the strategy. Everything would have worked out
fine if Gaël were completely in control of counting backwards
(or subtraction of 1), because he started with 41 which gives
too big a result. He tries another method-a correct one-but he
doesn't have it at all under control at the moment and tries 45,
which puts him further from the goal, so he corrects it and tries
40 (the only number that he can easily put in the neighborhood
of 41 that is smaller than 41). It seems reasonable to think
that he is using as a principle of correction : "if a bigger
number puts me further away, then a smaller number will put me
closer" which implies that he postulates that the application
is monotone. And 40 produces an exciting result: he is really
close. It seems reasonable to think that for Gaël the result
confirms the validity of his intuition: "the proof"
, and on top of that that he sees that he has to take 1 from 40.
Which would imply that he registers that a correction of 1 in
the choice changes the total by 1 in the same direction. The theorem
will work for 2 in just a moment. It probably wouldn't work for
8 or 10. But Gaël doesn't know how to find the number before
40-he subtracts 10 and adds a unit: 31-failure. Return
to the previous strategy: bounding. Gaël increases the lower
numbers-31..33...34- and decreases the upper ones-43...42...Even
if the upper ones stay above 40 this could work...where has he
gotten to?
This time he successfully uses the theorem of conservation of
differences in a numerical translation (the difference between
the two total results is equal to the difference between between
the numbers tried.) But he only succeeds because he doesn't have
to get past a multiple of ten.
The first success of the exercise is celebrated as it should
be with a free chat, in the course of which Gaël announces
that he would like to play the bag game again and learn to find
the number-to figure it out. The tutor offers it "right
away" and Gaël says "Yes". "With small
numbers, then, because you're tired."
There are 7 pieces, some of them triangles and some rectangles.
Gaël counts 3 triangles and puts everything in the bag.
"How many rectangles are there?", asks the tutor.
"7"
"No. 7 altogether..."
"How many rectangles are there? There are 3!" , Gaël declares.
"You want to bet?"
Gaël hesitates, wonders a bit.
"You can draw them to figure it out..."
He draws 3 triangles, then before drawing the rectangles announces
"Four".
The tutor tells him to draw them, but he can't remember the shape
any more, and has to feel them through the bag to remind himself.
He re-counts after making the rectangles.
This last episode in the observation is important, because
it shows, brought out by fatigue, Gaël's difficulties in
associating a number with what it represents. He did observe the
different classes of objects and he did count the objects, but
he seems to run into a barrier in getting from one notion to
the other. To a large extent it is this laborious passage which
causes his hesitations: he often gets stuck on the classification
side, then when he finds way to count them, he no longer knows
what his point of departure was.
One source of difficulties may be the proximity of the numbers-here
3 and 4. Thus we took care in preparing the materials for the
session to provide cardinals of fairly different sizes: 45 -
7, then 39 - 13 (except that for the initial phase we had 26
- 26, and that was a mistake).
2.2 Observations on Gaël's difficulties
This session brought out some of Gaël's long-standing difficulties with numeration: difficulty making a durable assignment of a cardinal to a collection and difficulty managing several numbers at the same time, especially if they are invisible, but even if they are not.
In numeration, also difficulty with the "privileged role" of the number 10, which crops up frequently inappropriately as a fetish number. On this subject one can make the following remark: the privileged role played by the number 10 in numeration, in calculation of sums with carrying or differences with borrowing or multiplication, must seem to a child who is not up on things to be essentially magic.
Difficulty getting past the multiples of 10 in counting backwards
and thus in ordering the names of the numbers.
Obviously, we also observed some other difficulties, such as
for instance the perfectly natural one of sustaining his attention
at times, but we do not intend to discuss those here.
2.3 Effects of the session
Are we now able to answer some of the questions we asked ourselves
before the session?
For a start, it seems perfectly clear that Gaël is completely
capable of entering into an action situation. He accepted progressively
the rules of the game which consisted of taking charge of an objective
and of the means of verifying by himself that had been achieved,
of hazarding solutions and of checking them against the state
of the milieu. He took over progressively the search for a good
answer, rejecting contradictions and inadequate solutions himself.
He took pleasure in the game of predicting and verifying even
when he didn't win.
He engaged voluntarily in going the route of anticipation. This last point is very important for more than one reason
Anticipation is the first step towards creation of a theory and
passage to an experimental basis: the subject gives up the procedural
mode, with only direct interactions with the milieu, and the trial
and error method and sets himself at a distance from his actions.
This reflexive attitude leads him to a declarative mode.
Anticipation rests on the existence of at least an implicit model,
true or false, on which it is based and the expression of which
permits it to be put to the test. Here the model is the relationship:
number known + number tried = 52, and it seems sure enough to
Gaël to permit him a rapid simulation of the experiment (it
is never put to the question, at least as regards its validity.)
It is interesting to note that Gaël did indeed master the
steps of anticipation: we wanted him to interest himself in the
material nature of the givens of the problem statement; we produced
the collections in question with a bizarre and captivating ceremony
so as to augment the affective, perceptive and sensorial weight
of the search for a solution. Now, investment in application is
in a way antagonistic to investment in action, in the sense that
it assumes at least a provisional refusal. Here, Gaël is
to renounce the pleasures of action, of decision, of betting,
of the game, to replace them by calculations and simulations.
But in any case, it should be remarked that anticipation inherits
to a certain extent the motivation associated with the situation
that it simulates. Gaël experiments with his predictions
with the little shiver of pleasure recalling the one he feels
at the moment of betting.
Finally, the successive consideration of several possible predictions in the course of a single bet, and the fact of writing them permits the examination at the same time of diverse choices and consequently the choice of a strategy based on the structure of this universe of possibilities.
The passage from a "contingent" prediction where the
subject doesn't conceive of the situation as having any other
issue than the one envisaged to a prediction of possibilities
is an indispensable step towards the emergence of a "prediction"
of the necessary where the issue is predicted from among others
for reasons of logic or mathematics or something different but
theoretical.
Gaël is thus capable of entering into all these phases of
the dialectic of action, of producing and checking implicit models,
even though, as we shall see below, the efficacy is still a bit
weak. He probably accomplished this activity naturally, which
would explain the normal development he can be observed to have
had. His stereotypical attitudes which can be observed in class
and his tendency to search for easy answers by interpreting the
suggestions of the adult are thus an effect of his manner of using
the didactical situation.
We were able to see here that this situation is not ineluctable.
The choice of an appropriate situation did indeed produce the
rupture we envisaged, with the efforts predicted. To be sure,
this "accidental" rupture has not yet changed Gaël,
nor his relationship with knowledge. It was partly obtained by
making use of his major fault: the desire to seduce the adult
and maintain affective and playful relations with him. This
game with knowledge needs to be regularly installed and to persist
in ordinary didactical circumstances. In fact, there is no question
of asking Gaël's teacher to modify her pedagogic methods
which are working for lots of other students and which no doubt
offer many similar occasions which Gaël simply doesn't grasp.
2.4 Projects
What we must do thus is to study the means of engaging Gaël
in this route and of giving him the taste and the means of seeing
to his learning.
There is also a lot left to do to get him to master situations
of subtraction and give them some sense.
Gaël has no problem whatever in envisaging the sets present.
He manages without difficulty to isolate the triangles and the
"non-triangles" and include them in the starting collection,
whether or not the "non-triangles" have a clear common
property (squares and circles...)
One could suppose that it would suffice for him to associate
with these set operations the corresponding numerical operations
inverse to each other, addition and subtraction.
Certain didactical methods thus consist of illustrating one or
another case by a set of examples and problems, sufficient to
suggest the field of operation of each one. In these methods the
procedures of calculation, the implicit model and the theory never
change in the course of learning; it's a question of associating
an already made mathematical structure with some situations assumed
understood or understandable and it is these situations which
constitute the meaning of mathematical operations.
These methods are based on conceptions of significance and learning
which are fairly old and much discussed... With a lot of simplification,
they can be summed up as follows:
The set of realizations of a piece of knowledge or a theory, that
is, the objective situations in which it turns out to be valid,
constitute what it signifies. To give a meaning to a structure
means to find some applications for it-places where it can be
used.
A piece of theoretical knowledge, to be learned, must be constituted
from knowledge already known and by a discourse or by logical
(or mathematical or scientific or rational,...) means which are
themselves already known, or in fact "learned" directly
ready made (in the sense of committing it to memory), for example
as an algorithm. Giving a meaning in the latter case comes down
to making it correspond to problems or situations where it is
realized, that is, where the objects it talks about are present
or the relationships it envisages are true. Teaching will consist
of producing conditions to associate the two after one or the
other has been memorized.
Generally, in lots of cases the process of learning leads back,
even though with diverse justifications, to conditioning: whether
one is starting with the theory and looking for its applications
or starting with cases and hoping to produce an abstraction to
the structure or both.
This association does not work out too well, because the interpretation
of the situation doesn't get produced unless the complete theoretical
schema is known and inversely the theory cannot be well understood
if it has neither a justification nor any explicative or descriptive
function. The miraculous and a-historical adaptation of the theory
to the hoped-for practices is an obstacle to partial learning.
The theory must be learned in its definitive and correct form,
adapted to complex, advanced examples to which it is to be applied.
The best one can do is to chop the theory into simple bits and
look for simplified situations where these bits by themselves
take on the value of theory or application...always a perfectly
adapted one. But whether one chops or not, it always comes down
to needing to associate two pieces of knowledge which have already
been "achieved" learned or constituted independently
of each other.
To palliate the difficulties of learning this association (unmotivated
for the student and reposing entirely on didactical decision)
the teacher can refine the method by introducing illustrations
(manipulations, schemas, mnemotechnical discourses) designed to
emphasize the association, but not producing any advance in either
of the two.
Here, one could "teach" Gaël the elements he lacks:
make a plan, identify in a given situation an appropriate plan,
solidify subtraction by the repetition of manipulations and the
association of an appropriate discourse: "I take away, I
re-group, ..."
On the other hand, what we are trying to do here is to get Gaël
to construct and learn a theory using a different process, an
historical one.
We are going to consider a different component of the meaning
of subtraction.
For example, to take 5 from 57 one can count backwards, possibly counting on fingers in order to stop at five: 56 55 54 53 52
1 2 3 4 5
To be sure, it is more complicated as a procedure, but the child
can keep a tight connection between the representatives of the
numbers and the names of the numbers being counted off. It is
thus more economical (or more primitive as far as theoretical
knowledge goes) . In any case, it is impracticable if it's a
question of subtracting 39 from 57.
One can maintain on the theoretical front that if a + b = c it is logically equivalent to take a or b from c, but it is clearly not true in the present case: to take 52 from 57 it would be necessary to "invent" another system and count from 52 to 57 counting on the fingers or otherwise the missing elements: 52 53 54 55 56 57
1 2 3 4 5
It is well known that the moment the objects are no longer physically
present this method breaks down because the student no longer
knows whether to "count 1 with the 52 or the 53". Certainly
in the classical methods of teaching the teacher made sure always
to examine "all the meanings" of differences: what is
missing, what is left, what there is too much of, or too little
of,...etc., but always flatly, as facets of the same piece of
knowledge, and without worrying about the adaptation of these
points of view, nor about their place in a genesis of communication.
The method Gaël uses here is different and based on a better knowledge of the ordered set of natural numbers and of their orders of magnitude. To find what needs to be added to 39 to get 57, it consists of taking a number close to the result on which the calculations are simple, for example 20, then making corrections with the aid of the theorem of the conservation of differences:
39 + 20 = 59, which is 2 more than 57, so it is enough to add
20 - 2 = 18. This method is much used in mental calculation. Clearly
it is not a "method" for Gaël-it can't be put to
use whatever the situation that arises, it is not recognized as
such and it is not even a piece of knowledge: Gaël would
not be able to tell his father what he learned in the second session.
A whole process would be needed to turn it into an object of
knowledge which is efficient, conscious and well mastered at the
theoretical level.
And for all that, this method stumbles over Gaël's old difficulties
with numeration. We could well believe that we re seeing here
how a defect in the acquisition of an old notion can render impossible
an activity which is essential for the acquisition of a new notion.
But in fact, no, we are not in the presence of a real situation
of the learning of numeration. Though Gaël has little
grasp of the situation as an occasion for learning subtraction
because he is unaware of the didactical intentions of the tutor
and what the object of his didactical desire is, it is clear to
him that he is tripping over the possibility of counting certain
numbers (finding a predecessor to 40). That is what is keeping
him from establishing an efficient strategy. No question that
when by some other means he finds 39, that answer is going to
take its place also as the answer to "What is the predecessor
to 40?"
It would be possible to "didactify" this part of the
learning: recognize the difficulty, recall the means to surmount
it, re-explain, do some exercises in counting backwards, etc.
We are not going to do it. But to point out clearly the didactical
character of Gaël's difficulties, we arranged a short sequence
of this type at the end of the next session.
To return to a plan for the learning of subtraction, other strategies appear in other conditions (with other numbers) but with the same basic situation:
for example, from 39 to 40 - 1, from 40 to 50 - 10, 10 and 1 eleven
and from 50 to 57; 11 and 7: 18. This method, the most widespread
in mental calculations, is also based on order and decimal numeration.
It gets more efficient for larger differences. The standard algorithm
can appear as a shortcut for this procedure or as the result of
some other reasoning. Learning it could be organized as a frequent
presentation of the same didactical situation where the only thing
varying was certain conditions favoring the constitution of these
strategies. The possibility of replacing one by the other will
confer upon them a certain equivalence (from the point of view
of meaning), the choice of one or the other depending on its utility
or efficacy. These strategies mobilize all the fundamental schemas
of sums and differences. The order of their apparition constitutes
a genesis (good or bad) of the concept and gives them a meaning.
We will not evoke here the processes of formulation, validation
or institutionalization which will permit the emergence of subtraction
as a theory at the disposition of the child.
In the third session we are going to take up the same situation
again.
3.1 Session and observations
The tutor takes up the guessing game from the last session without
any modifications: there are 56 pieces which Gaël counts
and puts in a bag after having written the number on a sheet of
paper. The tutor then takes 10 big circles out of the bag, has
Gaël count them, then puts them in another bag along with
the first bag. The question is how many pieces there are in the
inside little bag.
Gaël thinks a bit, counts to ten and says "5!"
The tutor shows him the 10 circles, then shakes the other bag
and asks if he really believes there are only five in there. Gaël
smiles, blinks and shakes his head, acknowledging that he has
made a mistake. In fact, Gaël has just reproduced his habitual
mode of response: he counts to ten-stereotypical behavior-then
since he has to give an answer, gives a random one.
The tutor does not accept this response. In class, the teacher
cannot make this kind of stubborn demand of every student for
every problem.
Gaël then follows up in a mutter: "56...then there
are 10...(he counts to 40), I'm up to 40 and 10 are taken away,...that
makes 40!" In fact, he hasn't changed procedures, he has
just given a more plausible number to live up to the adult's expectations.
The fact that the number to subtract is ten, the magic number,
may contribute to this disarray.
The tutor then reminds him of the principle of verification of
the statements during the last session: "We made a bet and
we checked if we were right"...without, of course, saying
what operation was used. While he is doing so, the child, smiling,
thinks, then exclaims: "46!"
It seems clear that he is sure of his answer. It seems possible
that reminding him of the conditions of the situation has been
enough to make it possible for him to check his answer and thus
to produce a correct one. It also seems possible that Gaël
was playing a subtler game, throwing out provisional answers to
gain time to think it over, or even simulating his habitual response
to tease the instructor. In any case, this scene demonstrates
Gaël's need to "decorate the silence".
T: (slightly jolted by the rapidity of the response) " How come you're saying that makes 46?"
G: "Because I know that you take 5 from 10 and that makes 4 and that leaves 6 so that makes 46."
T: "!!!"
Doubtless the way to translate this answer is: from 5 tens we
subtract one ten (formula backwards), and that leaves 4. In 56
there are 5 tens and 6 ones; these 6 ones together with the 4
tens give us 46.
Here Gaël is directly using the resources of numeration
to effect his subtraction by the system: 56 - 10 = (50 + 6) -
10 = (50 - 10) + 6 = 40 + 6 = 46. It is true that under these
conditions this method gives a simpler procedure than the one
which would have been necessary during the preceding session:
52 - 7 = (50 + 2) - 7 =(50 + 2) - (2 + 5) = (50 + 2 - 2) + 5
= 50 - 5 = (40 + 10 ) - 5 = 40 + (10 - 5) = 45. And despite that,
Gaël is already having trouble formulating his solution.
This difficulty manifests itself in the incapacity to designate
the order of the numbers in his statement and by the apparition
of an inversion in one of the relations ("take 5 from 10"
instead of "take one ten from five tens"). Things often
happen as if Gaël worked out the relations in two stages:
first the binary relationship and the pair on which it operates,
then the ordering of the pair. Likewise, for example, in 21 he
first grasps the pair, then the ordered pair (2,1); i.e. 2 "gadgets"
and 1 "thingey" then, if necessary, the order 2 tens
and one unit, i.e., 20 and 1.
After explaining his answer (46), Gaël sets out to verify it. But first the tutor asks if it isn't possible to know how many pieces there are without opening the bag. Gaël's reply: "Oh, no. There is no way of knowing."
The tutor then reminds him of the method used the time before,
when they considered that the bag had a certain number of pieces
and then added onto this number the number of the pieces spread
on the table: if no error had been made, the resulting number
was the total number of pieces. Gaël uses this method and
figures that in fact, this time he has not made a mistake. To
be absolutely sure of the result, they are going to empty the
bag and count all of the pieces, after betting, but Gaël
says he is not "absolutely sure" of winning.
Each one counts some of the pieces, with the tutor making stacks
of 10 pieces. At the point when between them they have counted
40 pieces, Gaël stops and says "Oh, I know I have lost."
but the tutor encourages him to continue, and at the end of the
count he realizes that he had it right.
An observer might be astonished to note that Gaël has forgotten
the thing that constituted the key-the engine for the anticipation
the previous time. But we know that one of Gaël's difficulties
arises from the fact that he doesn't remember what he did before
in mathematics. In addition, the suggestion had been made by the
tutor; Gaël contented himself with latching onto it to carry
out his project of prediction in the most satisfying manner (for
the tutor) by submission to the desire of the adult.. He, furthermore,
had done nothing to draw the child's attention to the procedure.
In the didactical contract, for each of them it was a means, not
a piece of knowledge "to be learned". It is thus, in
a way, satisfying to observe the "innocuity" of a non-institutionalized
suggestion. If the means of controlling had been "taught"
there would have been a danger of seeing it used as a systematic
means of finding the answer, and even in the best adapted form
of addition with a gap, it would have been a pity and undoubtedly
failure for the creation of meaning.
But on the other hand it is clear that Gaël immediately
goes about his business of predicting, betting and verifying.
For him, it would be really disappointing "that you can
know in advance". Even the proof is doubtful and Gaël
hangs onto his suspense ("Oh, I know I have lost") until
the last possible moment.
T: "Do you think you could find it if we did something else?"
G: " Maybe, but I'm not so sure" (Let's not take any
risks!)
They take out the little circles (5 of them)and put all the rest in the bag. Gaël agrees that there are still 56 pieces in the bag, and provides the following solution:
"There, I think I've got it! Over there we make 50, and
there there are 6 and if you take 5 from 6 that would be those
(pointing to the little circles) and then that leaves one, so
51!"
In this computation, apparently the child mentally set aside
5 stacks of 10 and saved the 6 "unit" elements from
which he was able to pull out 5. But what would he have done
if, for instance, there had been 76 little circles?
The tutor has him write the 51 and asks him to prove it without
counting.
Gaël: "There are still 5, that never changes."
T: "5 what? 5 tens?"
G: "Yes, that. If you take away 6, there would be 5 taken
away, no if you take away 5 there would only be one left. I put
the 5 there (small circles) that leaves one (bag) and 5 there."
The child has given a certain character of immutability to
the 5 tens : "That never changes". In 56 there are 50
and 6. If 6 are taken away (from 56) and we take away 5, that
leaves 1. Thus he is paying attention to those 6 elements, reassured
by the knowledge that nothing needs to happen to the other 50.
The tutor brings him back to the other method of verification,
adding 5 to the 51 which are supposed to be in the bag.
T: "What is it we do there, 51 and then...?
G: "That's it! I've got it! Since there are 51, we can count
and get the same number!"
He seems really pleased, because he has rediscovered the algorithm from the time
before and connected it up with the possibility of proof.
But it appears to be the case that this time he has perceived
the didactical intention-by way of the tutor's insistence.
Counting backwards: "Getting past the tens"
To give Gaël a chance to practice counting backwards, and
especially to get past the multiples of ten, the tutor uses the
same game.
There are still 56 objects in the bag, but he takes some of them
out (one by one, at first) and at a certain moment he says "tok"
and the child is supposed to say how many are left in the bag.
To get him to understand the rules of the game, he takes the
bag, doesn't take anything out, and says "tok". The
child says "56". Then he takes out 1 and says "tok".
Gaël hesitates, then says "55". The tutor continues,
taking out 2. Gaël makes no mistakes and says 53, but when
3 more are taken out, he says "40". So they bet a caramel,
Gaël counts up from 40, adding on the objects outside the
bag. Arriving at 46 he says he has won.
The tutor points out that there were 56, and they start again.
When there are 50 pieces in the bag, he takes out 3, but the
child does not appear to follow the action.
(Decidedly, as long as the tens place never changed, from 56
to 50, there was no problem whatever in counting in reverse.
The difficulty that completely blocks Gaël is that of getting
from one tens place to another.)
Gaël is a little lost, but ultimately discovers the solution
and successively designates the last 3 elements, counting : 49,48,47.
The game continues, with a "tok" at 43 which gives
him no trouble at all. Then the tutor takes out 3 and Gaël
says "39". He bets, verifies by adding 3 to 39, then
says to himself "There aren't 39. What could it be, then?"
He counts backwards and finds 40-number confirmed by verification.
The game continues thus for a few minutes, but the tutor starts
taking out the elements by tens and Gaël has not trouble
at all giving the result, ending the session with a success.
3.2. Summary of the results
The return of the "game" of the bags with slightly
simpler givens permitted Gaël to rediscover the initial schema
and produce the expected reasoning. We also discovered difficulties
and errors of his that we had already known about. Repetition
of situations of this sort would unquestionably permit us to lead
him to correct his writing errors, to know numeration well and
to give some meaning to subtraction problems. Especially since
the tutor has managed to develop a pleasant relationship with
Gaël. There is no doubt whatever that to please the adult,
Gaël will identify what is pleasing to the adult, manifest
the expected behavior and simulate the desired acquisitions.
This will give him the time to cement the affective relations
which do not rest on the didactical contract and break off the
ones which might constrain him. But that is exactly the problem:
the price of his progress would be the reinforcement of exactly
what led to Gaël's failure. Gaël's relationships with
certainty show that it would be vain to continue in that direction.
3.3. Observations and analyses
Gaël's attitude of avoidance in the face of certainty which
is in itself surprising becomes more comprehensible if it is put
in relation to everything that particularizes his cognitive process.
From the beginning of the sessions we were struck by this profound
tendency of Gaël's to give more or less plausible spontaneous
answers. He seemed incapable of suspending his highly impulsive
reactions for a time in order to reflect, assemble information,
and slowly construct the necessary inferences. Briefly, one frequently
finds this difficulty in entering into processes which have been
made secondary.
What we can assume is that in the absence of a deficit on the
operational level, such an attitude has a meaning from the point
of view of the subject: through it, he pursues a satisfaction
or avoids something displeasing. What this behavior puts at a
distance during the learning process is the field of certainty.
We remarked earlier on the degree to which he was made uneasy
by being made to leave the domain of the possible for that of
the necessary.
Fleeing total mastery of the knowledge by avoiding all reasoning
in favor of answers given at random is in effect , for Gaël,
remaining in the domain of uncertainty. This tendency is so strong
that, sure of the result, he still tries, by a genuine denial,
to abolish the character of certainly from his reasoning: "Oh,
I know I have lost!"
We are therefore facing one of the most delicate points of a
didactical intervention of this type. The mathematical failure
appears here with its symptomatic significance, that is, it goes
back to the total organization of the subject and the current
equilibrium of his investments.
From that point, if the intervention takes the aspect of a re-education
in the strict sense, aiming at the disappearance of the symptom
by putting in operation diverse strategies-helping the child
to use reasoning, etc.-one courts the risk of failure; the counter-investment
of the child will come into play and the tutor will be powerless
to make a profound difference in the avoidance conducts of the
subject. It is equally possible to bring on compensations of
a negative sort to the extent that these attitudes play their
role of defense against anxiety.
Should we then adopt a clinical approach aimed at determining
the unconscious meaning of the avoidance behaviors which probably
translate into Gaël's processes in the domain of mathematics?
But such an approach is a particularly uncomfortable one. It
would be in the framework of an analytical therapy where all forms
of intellectual inhibition turn out to be particularly complex
and largely overdetermined symptoms. It is all the more so in
the framework of an intervention where material by way of projective
tests remains fragmentary and where everything which is a trait
of the history of the subject as well as of his intra-familial
relations remains for the most part unknown. The only hypotheses
with regard to the meaning to give to a symptom would rest entirely
on the psychological testing done before the first session. We
could. in fact, set up a relationship between the results of the
Rorschach and CAT tests and the symptomatic character of Gaël's
behavior; the fact of an otherwise well-balanced child showing
stupor and profound confusion when faced with certain situations
would have led us to the interpretation of an anxiety and strong
sense of guilt in the face of curiosity connected with the sexual
activity of his parents. One could, and various references in
psychoanalytical theory would authorize this, recognize in Gaël's
avoidance behavior a latent significance connected with the primitive
scene; maintaining uncertainty on the level of progress of the
thought process means insuring against the anguish of recognizing
the sexuality of the parents and confronting the sadistic impulses
connected with this knowledge.
But even if this interpretation were true, it would be totally
useless to us. Our project has nothing whatever to do with working
with the child to elucidate his oedipal conflicts; in a psychotherapeutic
field the didactical project disappears.
We will therefore restrict ourselves to the domain of the learning
of mathematics, but we will consider the mental functioning which
we have noted in its relations with the global organization, and
figure it into the economic equilibrium of the child. It is not
a matter of teaching the child to reason, but of giving him, in
the context of the mathematical activities which we are about
to discuss, the occasion to reinvest this function.
3.4 Projects of intervention-Situations to present to the student.
What are the didactical means that we know and that permit reasoning
to function? For the moment its not a question of their content
or of their methods, but of their motivation and especially of
their control by conviction.
Technically, the student's conviction about proof manifests,
confirms and strengthens itself in the four major types of didactical
situation, in a different form specific to each: in situations
of action, conviction is a affirmed by the confidence of the subject
in his anticipations. In situations of formulation, the fact
of communicating or expressing an idea doesn't necessarily imply
a high degree of confidence about it. But precisely what formulation
does is to produce an objectivation which plays an essential rôle
in the elaboration of conviction. The resulting distance between
what is said and what is thought, between a proposition and its
implicit truth value, between what is explicitly predicted and
what happens, raises the issue of the conviction of the speaker.
The situations in which judgments and proofs are expressed and
tested are situations of validation. Part of the convention of
this situation is that the subjects exchange opinions about a
fact and engage themselves in it. In general, the situations of
this nature which we propose set up a proponent and an opponent,
both of whom are students, in such a way that they elaborate a
system of proof-a theory-founded on intimate conviction and not
on authority. The search for truth is a demanding activity which
the searcher needs to maintain strongly enough to refuse to be
convinced by anything other than personal judgment while nonetheless
never refusing to examine any other argument. It must resist
authority, seduction, rhetoric, intimidation, social convention,
etc. And when it becomes clear that one's opinion is false, it
is also necessary to be able to repent, retract and again resist
the same difficulties. Difficulties which are legitimate, and
which tend to the establishment of reasonably stable truths of
which the persons who profess them take account by a sort of personal
engagement. Practicing situations of proof or validation permits
the subject to construct an interior interlocutor with whom he
can simulate debates along the lines he has learned.
In situations of institutionalization of knowledge, contrary
to the preceding, personal conviction is supported, shaken or
supplanted by reference to a norm exterior to the subject. His
conviction becomes simply a founded adhesion.
In the "problem-solving situations" in class in which
we had been told that Gaël participated well and found some
interesting Gaël can say whatever passes through his head
because he has confidence that the teacher will pull out what
he wants. Gaël can say things which he "sees" as
true without having to affirm that they are. This attitude may
be encouaged or even provokd by the group Socratic maietique methods
often used in classrooms.
What are the situations appropriate in the case of Gaël,
and which ones can be offered to him?
A classic method would consist of "exploiting" the
situation of action we created in sessions two and three, that
is, of pushing Gaël to take part, formulate declarations,
affirm them, retract them, in a relationship dual to the adult's.
The tutor would pul a moral out of each action of Gaël's
or having him pull one. For instance, he could repeat the betting
situations and insist : "You have to be certain! Are you
sure?..." We know that this method cannot succeed.
On the other hand, the tutor, being alone with Gaël, has
no way of organizing genuine situations of validation in which
the child is supposed to state his convictions to an equal. He
has to simulate them-and this perhaps might be valuable in that
a certain amount of identifying with the tutor might help Gaël
out of his "baby" rôle. But there is a danger
in that his tendency to stay in a superficial and playful relationship
with the adult could destroy any possibility of a debate about
knowledge. The playful attitudes consciously used by the tutor
risk being "recovered" to reproduce the fundamental
dilemma pointed out above.
The tutor therefore needs to accomplish a new modification of
the "didactical contract" , reintroducing some demands.
In fact, it is to be hoped that a sequence of ruptures can be
introduced; in alternation, the tutor could present himself as
a partner, an accomplice in a game, or else as an examiner who
expects something of him and who says what. It seems evident
in any case that the object of the teaching needs to stay hidden
to avoid immediate adherence and the submissive behavior we have
talked about.
We will come back to the game the tutor needs to give himself
up to in order increase and vary Gaël's positions about certainty
and uncertainty. But already, if one returns to the betting game,
one might possibly escape the recovery we alluded to without demanding
a change of attitude from the tutor: by multiplying the bets and
the number of givens present. That way, even if Gaël takes
some calculations as opportunities to evade the demands of certainty,
it's a good bet that he would not do them all wrong, if his knowledge
permits.
As far as content goes, it would be useful to continue the study
of numeration, the more so in that the natural follow-up of the
process engaged in with regard to subtraction would lead to the
construction and use of a system of symbolization of the quantities
present.. We will analyze the situations chosen from this point
of view after presenting them.
In the case of Gaël, what position could this partner occupy?
We know how much Gaël is dependent on affective climate,
to what point his attitude is determined by the other's. An attitude
of excessive affective neutrality will send him right back to
the stereotypical reactions of false intellectual activity; too
great a connivance will permit him a playful attitude where he
can behave childishly. It is essential to find the right distance.
What the tutor is aiming for is the right alloy of complicity,
where the mediation of knowledge and its own demands constantly
intervene.
4.1 Support
The tutor, as planned, starts off with an attitude which is a bit less neutral as regards the mathematical content, and a bit more didactical, though always encouraging. He is going to put on a little pressure. He and Gaël go over the exercises of the week from class. A notable one is an addition:
129
78
+136
352
Gaël says: "9+8, 17; +6 = 23. I write the 2 and carry the 3."
"Aha! I see what you did!" says the tutor. Gaël spots it too, unless it's that he deduces it on the basis that if it's not this solution it must be the other one, and he corrects it on the spot.
He finishes up the operation and writes the result, 343, writing the 4 backwards, which the tutor makes him correct by comparing it with the way he himself writes it
He observes that the mistakes Gel has made are mostly related
to numeration and the transformations connected with it.
Estimation Game
The tutor proposes to Gaël that they go back to the estimation
game. In preparation, they spread on the table 10 red pieces,
10 green ones, 9 blue ones and 6 yellow ones. On paper, the child
therefore writes these numbers arranged as follows
10 6
10
He puts them all in a bag. The tutor checks that he remembers
correctly how many of each color there are, then explains how
the game is going to go" Gaël is going to take a bunch
of objects out of the bag and his job is to figure out how many
of each color are left.
First try:
Gaël takes out two handfuls of elements, : 4 green, 2 yellow
and 1 blue, and tries to determine the number of green objects
left, which he manages very well by counting backwards. The tutor
than has him write down the result: 6 and write the name of the
color so as to remember what it's about. Same process for the
yellows, but when it comes to the reds he hesitates: did
he start with 9 or 10? He opts for 9, all because he thinks there
were 6 blues. The tutor suggests that he verify by recounting
the objects and that he write, so as not to forget:
9 blue 10 green 10 red
6 yellow
They put everything back in the bag and start again.
Here, clearly, Gaël is continuously under the control of the tutor, who intervenes frequently and makes decisions for him, but he keeps trying to get back to the game situation, seeming to want to get out of this didactical relationship.
The game aspect remains apparent, in spite of everything,
even though the operations predominate and the playful activities
themselves are put off a little: each time around Gaël has
to anticipate four different things.
The game of estimations has exactly the same structure as the
previous game, but the givens are ordered quadruples and the answers
likewise: for example, on the first try he is supposed to carry
out:
(9; 10; 6; 10) - (1; 0; 2; 4) = (8; 10; 4; 6)
For the child, the operation looks like a sequence of three subtractions, but Gaël has to keep the quantities in his memory by category: blue, red, yellow, green.
Relative to the previous game, this augmentation of complexity
(compensated for in part by the choice of small numbers) will
rapidly produce a problem with keeping the operations straight,
and thus with keeping track of the given representations.
But these are only "introductory" games. They are
there in order to introduce symbolic representations gradually
into the scene in conditions which will give them a determined
meaning, but it is assumed that these representations are known
to Gaël and the situation gives a conventional meaning.
For example, the tutor will have him make a table which clearly
prefigures numeration and which resolves this problem, starting
with the following round. Gaël already knows perfectly well
how to use the table, but part of what the tutor plans to talk
about is the justification of the table, which will therefore
take on an explicit and agreed-upon meaning.
If he had expected Gaël to realize for himself that such
a table was needed and to propose one, he would probably have
been disappointed: Gaël could perfectly well work the situation
out with the notation he used the first time, messy or not. Conditions
would have had to be a lot harder (larger number of sides, lots
of movements of the pieces, larger numbers) to justify and provoke
the invention of an accounting type procedure. The cognitive
profit from such a situation would have been minor relative to
the amount of energy and motivation it would have swallowed up.
Second try
The tutor proposes to Gaël that he should decide in advance
how many objects to take out of the bag. Gaël pulls out 7
objects and then determines exactly the quantity of elements of
each color remaining in the bag by looking at the numbers on the
paper and removing from them the objects spread out on the table
The tutor then suggests a "way of writing it that will save
time", namely the following table:
-"When you count them all, how many blues are there?" asks the tutor.
-"9"
-"Where are you going to write them?"
Gaël indicates the box and completes the whole line, thereby
"economizing on the writing".
From the didactical point of view, this scene is a transitional
phase designed to put the decor in place for a new learning situation.
The planned new situation is to be a phase of didactical institutionalization.
To prepare the way for this game, which is to simulate a known
game requiring the participation of the student at a "subordinate
" level relative to the "novelties" introduced,
the teacher communicates the rules of the new game...coming up.
In ordinary class situations, this game never appears except
in the form of a very closed exercise in applications.
And Gaël makes no mistake about it: as the amount of didactical
interference increases, Gaël passes progressively from his
lively, smiling attitude to one which is more serious and more
concentrated. Conscientiously he sets to work on the task, but,
always polite and even friendly, he enters into his position of
student learning under the baton of his teacher. It is time to
break this contract, which is comfortable and dangerous for Gaël,
and exchange the positions of the tutor and the student.
The Game of "Liar!"
They take up the game again, but this time it is the tutor who
takes the objects out of the bag, and furthermore he includes
a new element in the rules: they are going to play "Liar!"
Gaël doesn't know what that one is about, so the tutor explains:
- I am going to take out objects, and when I finish I will say
'There are this many greens, that many blues, etc. (in the bag)',
and if I am wrong you say "Liar!" If I succeed in lying,
I win, but if you succeed in trapping me when I lie, you win!
They try a first round: the tutor takes out a small bunch and states:
-There are 6 blues in the bag.
At his request, the child writes the number on the table and checks by counting backwards, starting with 10 and counting off the blue objects in sight. He agrees with the number stated.
-"There are 6 reds", the tutor next states.
-"6 reds" repeats Gaël, "6,7,8,9 (he adds in the reds spread on the table): "Liar!"
Gaël says this word with a little bit of concern and a lot
of pleasure. He smiles. It took him some audacity, even though
he knew that he had the license to do it. Under the fiction of
the game, Gaël enters the other role, that of interior interlocutor
mentioned earlier. The passage from one position to the other,
from declarer to judge, from liar to person responsible for the
truth...and above all the possibility of passing from one rôle
to another offers Gaël the means for a symbolic rupture with
his earlier position. This rupture, with respect to knowledge,
can be compared to that of the famous Fort-Da game of Freud.
The verification is done and yes! Gaël is right and the
tutor has been caught. Note that his "error" had been
a trick, and for Gaël the detection of the error has become
a game, done in a spirit of complicity and agreement rather than
aggression. There is more than one nuance between the classical
meaning of an error and the symbolic one that it takes on here.
Later on maybe Gaël will do some teasing himself and make
up his own "tricks".
They continue in the same way with the other colors, and the
child makes no mistakes, but as he goes along he hasn't written
on the table the objects removed and the objects remaining. The
tutor advises him to recapitulate: for the red ones, the number
stated was 6 and Gaël said "Liar!" To that 6, he
had added the 3 on the table, which had confirmed his judgment.
But he doesn't know any more what to do to get the 10 reds in
all. He has to be helped:
-"How many were there altogether?"
-10
-And how many there?" (on the table)
-3
-"So that leaves..."
-7
Note also that though Gaël keeps on making his "little
mistakes", the tutor is careful not to take him to task for
it and contents himself with getting Gaël to fix them. As
the situation gets more complex, and as there get to be more and
more occasions to examine differences or to carry out subtractions,
Gaël develops strategies which serve as the meaning of the
operation and uses them with more and more facility. Thus, to
check the validity of the statement "10 - 3 = 6" he
carries out 6 + 3 = 9.
Now Gaël no longer looks, as he did before, defeated in
the face of subtraction, with the sort of refusal that seemed
to appear in the previous sessions. He now manipulates them more
easily, though he is not able to use them in a systematic way
every time it's necessary or more or less useful Thus, when he
has 10 and 3 he knows that he has to "do 10 - 3" to
find what's "left" (the aim of subtraction) but when
he had 6 and then 9 and needed 10 the problem seemed totally different
to him.
The tutor then has him fill in the line of "take away's",
but he gets mixed up and writes 5 yellows instead of 5 greens.
The tutor has him correct that before asking him how, if he hadn't
corrected it, he could have spotted the error.
The table is as follows:
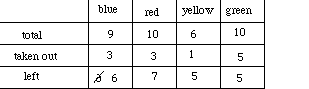
Gaël does not manage to provide the explanation requested, but that may be due to the fact that he has the complete table in front of him. Possibly if he had had only the column:
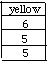
he could have come up with the correction. He has to be given
the solution.
The verification that we pointed out above is functioning implicitly,
but it is not perceived as a fact by Gaël, it is apparently
not something he would be able to formulate, and a fortiori
he can't use it to convince anybody, even a benevolent and attentive
interlocutor.
It is easy to see, thus, why the tutor had to propose addition
as a means of checking subtraction-Gaël probably would not
have invented it-why it was all right to propose it, because it
was not proposed as an object to be learned. It had a role and
meaning which were obvious in the situation, and it had simply
been made available to Gaël.
-and how Gaël appropriated this means and integrated it
into his procedures. From this point, it may be that creating
situations favoring making this explicit will suffice to get Gaël
to evoke the relations between addition and subtraction. Situations
of that sort assume that one has at least provisionally rejected
concrete means of proof-recourse to counting things-and consequently
that one operates on symbolic systems.
The tutor sets to work immediately preparing this new phase,
making a material separation between two system: that of the
collections which can be physically manipulated and that of the
writing used to talk about what happens to the former. This materialization
will give the two of them the means to recall this situation later
on.
Symbolization by labels
It's time for a new game: groups of objects are represented by pieces of paper. The tutor puts into one bag pieces of paper which represent the objects that Gaël is putting in the other: for example, he writes "6 green" on a piece of paper and Gaël puts 6 green objects in the bag. He makes a certain number of pieces of paper this way:

-" Can you tell me how many red objects I have in my bag?"
the tutor asks. You can't open my bag, but you can open yours"
-" Then I sure can!" , replies Gaël, opening his
bag with a big smile.
He finds a first piece of paper : 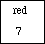 and
says ; "7 reds!"
and
says ; "7 reds!"
-"That's all?"
He then checks all the bits of paper and adds up the numbers
on all the ones indicating the color red: 7 + 5 + 5 = 17.
He writes 17 on the preceding table and then counts the other colors and writes those results up, too:
and
When the tutor asks if he is sure of the results he just got, the child looks hesitant and would really like to check. They re-count together. For the green ones he explains:
"6 and 3, 9. And 4...If we have 4, we take away one of them (to add onto the 9) that makes 10 and since we took one away there that makes 3 so that makes 13."
Then the tutor writes the number of objects that he is (theoretically)
taking out: 10 of each color, and Gaël unhesitatingly finds
the number left of each color.
4.2 Behavior expected in the course of these situations: uncertainty
and knowledge.
Gaël really dislikes renouncing the charms of uncertainty.
To understand how such an attitude can block the acquisition
of knowledge and how the situations we propose might operate,
it will be useful to look more closely at the relationships that
establish themselves between knowledge and uncertainty in a teaching
situation.
Knowledge manifests itself through a decision, or rather through
a choice among several decisions, or among several opinions.
For a student to be able to put a piece of knowledge into action,
he must therefore be offered situations which can have different
outcomes depending on the choice he himself makes as a function
of his knowledge. The meaning of the knowledge is made up, as
we said, of the spread of envisigable outcomes which it makes
it possible to reject. If a piece of knowledge permits the elimination
of all but one outcome, it permits a sure decision But it can
happen that knowledge about a subject lets several outcomes subsist,
with perhaps some preferences which could translate into probabilities
of choosing each outcome. We will then say that the situation
presents the subject with a certain uncertainty, larger or smaller
depending on the number of outcomes and their equiprobable character.
Learning a piece of knowledge manifests itself by the diminution
of the uncertainty in situations in which it is engaged (one
can even evaluate the quantity of information represented by a
piece of knowledge by the variation it produces in the uncertainty.)
In general, learning happens in a situation, motivated by the
desire of the subject to diminish his uncertainty.
Thus one can compare didactical situations to games. The teacher
communicates to the student a problem situation which puts on
the scene the objects in question, and gives what corresponds
to the rules: that is, the means the student is allowed to use
to obtain all possible states of the game. He fixes certain objectives,
that is, some results which are to be obtained following the rules
with, explicitly or implicitly, a reward. To be sure, the character
of these didactical games can vary a lot depending on the subjects
and the types of pedagogy chosen. In particular, on whether the
teacher is assumed to be supposed to communicate the strategies
for resolution from the start or the student is supposed to produce
them as a means of adapting himself. But the bottom line is that
at some point the activity of the student will consist, in the
face of a problem situation which presents him with a certain
uncertainty, of reducing the uncertainty by choosing a solution:
the student is not doing mathematics unless he is solving problems.
For all that, it would be false to believe that the acceptance
of the rules and the reduction of uncertainty is the only manifestation
of knowledge and acquisition. Information can augment the subject's
uncertainties by show ing him choices he hadn't thought about.
What he learns closes off some questions, but opens others.
The search for new situations, for questions or for new rules
- which increase uncertainty - is a tendancy inverse and complementary
to the one just discussed. The production of questions and the
production of answers are two very different manifestations of
knowledge and its genesis. They respond to each other "dialectically"
from one moment to the next in the epistomelogical subject, from
one notion to another in the organization of his knowledge and
finally between knowledge and the subject in the course of his
development. The search for new problems responds to different
motivations depending whether this dialectic is aimed at adapting
the world to the subject and the subject to the world (Piaget's
assimilation) or aimed at the internal transformation of the subject,
for his organization, his consitency and his own ergonomy (Piaget's
accomodation).
To understand the profound unity of this quest for knowledge,
let us examine from the point of view of the student the function
to which it responds.
To start with, the absence of uncertainty cannot be a stable state. In a way, the subject defines himself, exists in his own eyes with respect to a milieu by the modifications he can produce in it. A milieu which gives him no opportunity for action-that is, for decision or for choice-in effect denies his existence as an autonomous subject. This is in particular the case in closed situations. Inversely, but for the same reason, a purely random choice is not an expression of the subject and also fails to give him existence. One can thus imagine that the subject is always in search of situations which are either relatively open, which he can reduce by exercising the creation of knowledge and of his power of decision and action, or relatively closed and such that he can open them by the consideration of new variables and new rules.
Psychoanalysis gives a deeper analysis of this phenomenon and
permits the comprehension of the relations of knowledge considered
as a symbolic object with the motivations of the subject.
There remain four more sessions in which the tutor continues
to fight to introduce more and more difficulties and put Gaël
under the obligation of surmounting them. Every relationship
is governed by the same principle. The progress is not spectacular,
but it seems, after the fact, as if this fourth session had been
decisive.
The relationship which developed with the tutor and a certain
awakening of awareness of difficulties to avoid launched a new
attitude for Gaël.
Follow-up reports indicated that the child integrated well into
his class and rapidly filled in his mathematical gaps.
The general aims of the intervention were as follows:
a) At first to establish a climate of confidence: an agreeable
dual relationship which nonetheless took account of the difficulties
at issue.
b) At the second stage, to make use of this relationship to propose
to Gaël some didactical situations in which knowledge is
not to be found in either the discourse or the desire of the teacher,
but rather in a relationship with the milieu. These interactions
need to be motivated by the desire of the child himself, and lead
him to take on decisions specific to the knowledge to be mastered:
experiment, decide, search,...
c) At the third stage, by new ruptures with the didactical contract,
the issue was to get him to give a "price" to truth,
and possibly to prefer it to the comfort of a consensus: to choose,
for instance, to verify a result despite the discomfort of acknowledging
an error. It was obviously not a matter of producing a moralizing
lecture on the subject, but of obtaining these behaviors in an
effective way. We tried to get him in the habit of defining himself,
recognizing himself and pleasing himself as a constructor of knowledge
and the person responsible for his convictions, faced with the
facts or faced with others around him. We wanted him to experience
mathematical activities not as "the discovery of his mistakes",
"the recognition of failure", "the revelation of
his sins" or what's more as "the look into his parents'
bedroom" but as an exercise in equilibration, liberation
and foundation of "myself".
The reader should not be led astray by these formulations. It
is not a matter of psychotherapy but of didactique, that
is, of specific activities intentionally organized with a view
to the acquisition of specific knowledge. But it is necessary
to be aware of the psychological dimension of these interventions,
Gaël was one one of seven cases studied between 1976 and
1983. Some succeeded, some failed and some were partial successes.
But no characteristics common to all of the cases turned up, except
perhaps for the importance of their psycho-affective problems.
The tutor caught in a difficult relationship and the observers
surprised by massive failures of the student have a tendency to
concentrate their attention on the characteristics of the child
and not on the conditions of the situations confronting them.
A-didactical situations
In our first approach, we have nonetheless two opposite types
of reaction which struck us as important. These reactions can
only be observed when the child has accepted an activity for \which
he takes responsibility and where he can know on his own whether
he has succeeded or failed. In acknowledging that the results
do not conform to their predictions, certain children turn pale
and worry; they read this result as a personal failure and look
discouraged and guilty. Even if they get bravely back to work
, their behavior shows that the situation is having an internal
impact.
Others, on the other hand, seem to wake up suddenly: something
unexpected and interesting is happening; personal failure is gotten
past and minimized in favor of curiosity and an opening towards
the exterior.
These two opposite ways of reacting to learning situations (that
is, where the relationship with the adult is not directly an issue)
are relatively stable in the subjects, in time and the material
covered by different problems. The children in selective failure
whom we encountered all belonged to the first category.
Didactical situations
The second remark comes from contrasting the behaviors of Gaël
and Cyrille (with whom we had a partial success) in their relations
with the tutor. Both wanted to avoid a relationship they felt
to be conflictual. But they did it with diametrically opposed
strategies. The obligation to take responsibility to produce
one's own answer to a question proposed by an adult is a painful
experience for children who are failing. There are at least two
manners of avoiding it:
One consists of taking it excessively seriously, dramatizing
it as much as possible in a mode which we qualify metaphorically
as "obsessional" (Cyrille's type) The other, on the
other hand, consists of evading it to the largest degree possible
by simulating more or less adroitly a minimal participation (Gaël's
type).
Every question puts students of the first type into a worrisome
situation, or even a dangerous one, and sends them back to the
original situation. To escape from this grave aggression, they
must close the question immediately, no matter how, if necessary
knowing nothing about it at all. Leaning on the didactical contract,
they refuse to accept a question unless they already have the
solution in hand. They require the teacher to transform solutions
into algorithms, to state criteria for the use of an algorithm
and reassuring signs that they are on the right track-the assurance
that by memorizing everything that has been said in class they
can immediately respond to this horrible situation. And the more
they learn and the more good answers they have available, the
less chance they have of finding the right one.
For them others, nothing needs worrying about, nothing is serious,
everything is theater. In the collective phases they enter into
the game, answering with the others, taking risks-the teacher
is convinced that these are wide awake students with a good understanding.
They may even answer correctly at the moment, but if they are
personally interrogated, in writing, for instance, they don't
know it, haven't learned it, haven't hung on, they aren't concerned,
haven't stashed away any of it. They are agreeable and make no
trouble, but they are not there in person, and in the end they
learn nothing.
The one and the other, each in his own way avoids confronting
the learning situation.
The former lean heavily on the management of the didactical contract
and tend rapidly to petrify it. The latter are far harder to
spot in the classroom. The teacher doesn't notice until too late
that these "intelligent" and wide awake students have
failed their first composition, then their second...Incomprehensibly,
they know nothing.
Here are the provisional conclusions which we were able to pull
out of this work as of 1980:
In the course of a session whose objective is to teach a student
a specific piece of knowledge (a didactical situation)
the student interprets the situation presented to him, the questions
asked him, the information given him, and the constraints imposed
on him as a function of whatever it is that the teacher reproduces,
consciously or not, in a repetitive way in his teaching practice.
We are particularly interested in whatever amongst these habits
is specific to the knowledge being taught: we give the name "didactica
l contract" to the set of (specific) behaviors of the
teacher which are expected by the student and the set of behaviors
of the student which are expected by the teacher.
Present in this question, this "contract" rules the
relations of teacher and student on the subject of projects, objectives,
decisions, actions and didactical evaluations. It is the "contract"
that specifies the reciprocal positions of the participants on
the subject of the task, and which specifies the deep meaning
of the action under way, of the formulation or of the explanations
furnished: what do we need to know? How are we going to tell if
we have succeeded? What are we supposed to do if we haven't succeeded?
What should we have known to succeed? What are we supposed to
say? What else could we have done? What would have been a mistake?
What are we supposed to learn? How can we learn it? How can we
remember it?, etc. It is the "contract" which explicitly
fixes the role of knowledge, of learning, of memory, etc.
It is through the rule of decoding didactical activity that scholastic
learning passes. One can think that at each instant the activities
in a process depend on the meaning he gives to the situation
proposed him, and that this meaning depends heavily on the result
of the repeated actions of the didactical contract.
The didactical contract thus presents itself as the trace left
by the habitual requirements of the teacher (requirements more
or less clearly perceived) about a particular situation. The
articulation between the habitual or permanent and what is specific
to the knowledge aimed at may be better or worse; certain didactical
contracts favor the specific functioning of the knowledge to be
acquired, others not; certain children read (or don't) the didactical
intentions of the teacher and have (or don't) the possibility
of pulling out a favorable learning situation.
Might it not be the case that certain didactical contracts prevent
certain children from entering into the process of learning?
The causes of failure should then be sought for in the relationship
of the student to knowing and in the didactical situations, and
not in his aptitudes or in his permanent general characteristics.
These contracts reveal the idea which teachers and students have
of the functioning of mathematics (of its creation, of its use,...)
In choosing a didactical situation (that is, a problem situation,
objectives for the student, information to give, objectives for
the teacher, etc.) to teach a certain piece of knowledge, the
teacher produces, whether he wishes or not, an image of the real
situations (historical, cultural,...) in which this knowledge
functions (was discovered, is used...) which is often quit distorted.
It is the circumstances in which the knowledge is used which
gives it its meaning. Thus a piece of mathematical knowledge does
not have the same meaning for a student and for a mathematician.
We give the name "didactica l transposition" to
the passage from one to the other.
The theory of didactical situations has as its objective to furnish
the means of controlling these didactical transpositions. Didactical
transposition depends fundamentally on the conceptions the teachers
have about mathematical thought. In their teaching activities,
teachers are thus obligated to use in a more or less explicit
way a sort of theory of knowledge, of the epistemology of mathematics.
These conceptions, used strictly professionally, are generally
not of a scientific character (nor even consistent), even though
locally they are the traces of more or less recent theories. We
give the name of "mathematical scholarly thought" to
these pseudo-theories.
The teacher teaches this "philosophy" along with the
mathematics and since it is not a good description of the appropriation
of knowledge, might it explain certain failures?
A good example of such errors is to be found in the book of Mme.
Jaulin-Mannoni, Le Pourquoi en Mathématiques ("The
Why in Mathematics") The first part is a very interesting
theory of comprehension containing a lot of good ideas. The second
presents cases of re-education-laudable effort-but it is not possible
to see, for example, how such a discourse attempts to adapt itself
in the case of Nadine to a perfect conditioning. The analysis
of this reeducation can be found in (???)
Always in the work of the last three years we have prepared the way for a study of these new hypotheses taking into account the set of these interactions and of these systems, and using theoretical studies of didactical situations and processes.
By way of a conclusion
In the observations which we have just reported, we have-like
most researchers before us-started off with a profile of the child
and the personal factors leading to failure, or connected with
its effects, this failure being considered nearly always as a
pathological phenomenon attached to child.
This conception corresponds very well to the strongest of the three modes of responding to failure :
Each of these three modes of response is supported by hypotheses
on different causes of failure in mathematics, but very few are
accompanied by a usable method of research.
I have wondered for a long time whether these hypotheses on the
instrumental origin of certain difficulties in calculation might
not be complacently welcomed principally because they justify
certain interventions expected by the parents and probably useful
to the children (for other reasons) but lucrative for others.
Certainly astonishing are the persistence and periodic return
of thundering but manifestly false or excessive declarations imputing
to the schools responsibility for phenomena for which the entire
of society in general is notoriously responsible.
No one form of scholastic difficulty seems to provoke so many
passionate reactions, nor to sustain as many prejudgments as failure
in mathematics.
Curiously, amongst a mass of publications of opinions, the scarcity
of objective works is striking, as if the complexity of the task,
or the forces resisting the work had inhibited all scientific
research.
It is true that the systems whose functioning or dysfunctioning
may play a role in this phenomenon are numerous, and their interactions
complex: the child, the parents, the teachers, the school, society,
the discipline can be implicated in the course of very diverse
approaches: cognitive, psychological or even psychoanalytical,
pedagogical or sociological. The economic rewards of these relations
are sometimes large and have contributed to the development of
a tangle of subjective value judgments such as to bewilder the
observer.
Although this complexity cam stimulate the imagination of innovators
wanting to help children in difficulty or of polemicists, it can
legitimately discourage the researcher who may fear the sterility
of a too restrictive hypothesis or the nasty surprises of a terrain
which is prey to ideology.
We hope nonetheless that the current research will soon permit
a little orientation of the debate.