"What do you think about Calculus Reform?" Drop that question into a group of mathematicians with educational leanings here in the United States and you are guaranteed an instant, lively-occasionally even acrimonious-conversation, with strongly held opinions of a variety of natures. To achieve the same effect in France, the query would be "What do you think of Didactique?"

Didactique is a program of research in mathematics education founded in the early 70's by Guy Brousseau and Gerard Vergnaud. It is a strong and lively program, and one which deserves much more notice than it has yet received in the United States. I have been interested and involved in both Calculus Reform and Didactique for a considerable period, but have only recently found a bridge linking the two. That bridge is a course developed by Marc Legrand of the University of Grenoble which he calls "Calculus by Scientific Debate." Legrand has long been active in the Didactique, and in designing his course he made clear connections with a number of the most basic issues in the field. In this paper I shall describe those issues by relating them to the motivation for the course and to specific elements in the course as Legrand presents them.

In his article on Mathematics , myth or reality [Legrand, 1995], Legrand provides an example whose implications disturb him greatly. (Note that here, as later, my translation is somewhat free, a liberty I have taken on the basis of conversations with Legrand.)

For several years in a row, we have given the following question to students entering at the calculus level (i.e., students with a strong background in high school mathematics) :

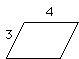
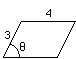
What is the area, A, of the parallelogram below, which has sides of length 3 meters and 4 meters?

The majority of these students give a firm answer: A = 12 square meters!!!

And a certain number of well trained students spontaneously provide a proof:

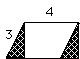
Legrand is distressed by the students' failure to think of

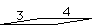possibilities like , or even , in which the answer 12 square meters becomes totally absurd.

This he attributes to the fact that the students are never faced with that problem in that format. Instead, in school the problem would be posed as:

What is the area, A, of the parallelogram below, which has sides of length 3 meters and 4 meters?

which gives the students no difficulty.

The situation represented by that example and the corresponding implications about what we are teaching our students to be "good at" provided part of Legrand's specific stimulus for developing his method. The analysis both of the situation and of what to do about it owed a large amount to Didactique. Here, then, is our first introduction to one of the major elements of Didactique -the question of didactical transposition. Loosely defined, didactical transposition is the process of converting a body of knowledge as it exists in its own right into a body of material that can be taught. One of the more visible examples in the United States, for example, has been our practice of separating pre-college mathematics into Algebra I, Algebra II, Geometry and Pre-Calculus-a practice which is now being widely called into question. A more extreme case, and currently one of those most discussed in the educational community, results from systemic reliance on standardized testing: teachers are under heavy pressure to teach the topics and tactics which enable their students to succeed on multiple choice tests. To whatever extent the teacher succumbs to this pressure, mathematics becomes, in the minds both of the teacher and the students, a field made up of bite-sized right-or-wrong tidbits. Other examples are subtler, but thereby possibly yet more deadly. For instance, any teacher worth her salt wants to enable her students to learn as much as they possibly can. It is a source of great-and highly legitimate-satisfaction to see one's students successfully responding to one's questions. But lurking behind that fact is the absolutely inevitable temptation to put in just a few more hints and careful phrasings so as to save them (and us) the pain of revealing the holes in their knowledge. The parallelogram problem seems fairly squarely situated in this area. Similar examples from further on in calculus are easy to unearth. How often, for instance, do we give students a max/min problem without giving them exactly the boundary conditions they need-with none omitted, and certainly no spare information to trip on?

The above remarks should not, however, lead one to the conclusion that the solution is to eliminate the didactical transposition-or even that it is all bad. In the words of Guy Brousseau, "It has its uses, its inconveniences and its rôle, even for the construction of science. It is at the same time inevitable, necessary and, in a sense, regrettable. It must be kept under surveillance." [Brousseau (1997)] Much effort has already been devoted to the study of this particular issue, in particular Yves Chevellard. [see, for instance, Chevellard and Johsua (1982).]

Other didactical issues are also involved here. One is the one Legrand states as an epistemological principle:

A person who has not had sufficient occasion actually to play, in its full grandeur, a genuine game of science has very little chance of interesting himself in the essential reasoning process of science, of understanding what the results of this reasoning really have to offer (understanding the power, but also the limitations, of its algorithms and modes of thought), and consequently of finding relevant ways of using those results to find a scientific solution to his own problems. [Legrand,1995]

What does it mean to "play a genuine game of science"? Legrand is not talking about the amusing or competitive aspect of a "game." The issue is involvement- active participation in an situation whose outcome is not pre-determined. Here, for example, is a description of one of Legrand's classes early in the stages of working on integration:

This debate took place in an "amphi" consisting of a hundred or so students with high school honors in physics/math (which means that they didn't detest math, but were probably mostly heading into physics.)

With a view to establishing a common basis for working with integrals (which had been introduced in a variety of ways in the sections the students attended the previous semester) the idea in this section of the course, leading up to generalized integrals, was to synthesize the basic properties of the Riemann integral of bounded functions on a compact real interval.

After having discussed different methods of extending the definition of measure (naively defined on "simple sets" of R2 as the sum of the areas of its constituent rectangles ) "an agreement was made" to take Riemann's definition: "A bounded domain W in R2 will be considered to be measurable if and only if for every e it is possible to find two simple sets which bound it above and below and which have measures differing by less than e ."

The measure of such a set can equally well be taken to be the upper bound of the measures of the interior simple sets or the lower bound of the measures of the exterior simple sets.

To test the effectiveness of the general agreement to this definition, the teacher then proposed the study of the measurability of the set W in the form of a comb whose teeth are approaching the y-axis, defined by:

W = »W i , for i³0, where W i = 1/i ¥ (0,1) for i³ 1 and W 0 = 0 ¥ (0,1)

The students were given five minutes to think about this alone or with their immediate neighbors. The teacher stood by silently, refraining from responding to this or that group who asked for his opinion.

At the end of this time of quasi-individual problem-solving, student opinion was solicited by way of a vote, and the results displayed on the board as follows:

-W is a measurable set and has measure 0: c. 1/2 of the class

-W is not measurable: c. 1/3 of the class

-impossible to decide: the rest.

Then the debate began:

-first student: "W is not measurable! Because to find a simple set containing W you would have to have an infinite number of rectangles because there are an infinite number of Wi's; but the definition states clearly that a simple set is finite union of rectangles. Hence W is not measurable!"

-second student: ""On the contrary, I think it is measurable, because all you have to do is take as the exterior rectangles the sets W i, and that shows that mes(W )= 0! We have W = »W i , and mes (W i ) = 0 for all i, so mes (W ) = S mes(W i ) = S 0=0 !!"

-third student:: "I don't agree! All you can say is that W is contained in the square [0,1] ¥ [0,1] and contains the rectangle W 0 , but you can't conclude anything from that, because one has measure 0 and the other has measure 1."

-fourth student: "Yes, but I can make a better bound! I take Q= [0,1/2] ¥ [0,1] and then you have W Ã Q»W 1 , so 0 ² mes (W )² 1/2."

-"And you can go on!", says another student

The teacher asks if it is possible to bound W within 10-15, and after several students respond with a "yes!", he writes under their dictation:

W Ã [0,10-15] ¥ [0,1] »W ₍₁₀ -15_-1) »... »W1 , and it follows that

mes W²10-15 +0+0+...+0 = 10-15 .

The conclusion the teacher institutionalizes is thus : "The set W is measurable and has measure 0".

At this point, another student steps in: "I'd like to go back to that argument we carried out back there!"

He indicates the calculation still written on the board: "mes (W ) = S mes(W i ) = S 0 = 0 ", which no one had pointed out explicitly (though the professor thought he had heard a few murmurs of protest at the moment when it was proposed.)

"By that reasoning I can show that the square A = [0,1] ¥ [0,1] has measure zero, because A = »W1/x - and that is impossible."

Total silence in the amphi (to the internal satisfaction of the teacher because he has a feeling this episode has a chance of jogging the students into consciousness of the distinction between treatment of the finite and infinite), and after a discussion of this apparent paradox, institutionalization of the necessity of caution in dealing with the indefinite iteration of the elementary mathematical operation "addition of numbers":

"If without defining the generalization we use the notation SieN, when card(N) becomes infinite, we are logically lead to write 0+0+...+0 = 0. We will thus be able to show that any set, being a union of its points, is measurable and of measure zero. And finally we can deduce very logically from that that 1 = 0! And that would put all the mathematicians in the world on the unemployment list."

We agree thus that, in the absence of ample justification, we will reject any reasoning based on a direct generalization of elementary rules for finite sums.

[Legrand,1990]

As is clear from this excerpt, Calculus by Debate certainly satisfies Legrand's epistemological principle that students should take an active part in sorting out their scientific progress. Before going further into how he achieves a state in which this kind of active participation can occur, I would like to point out another didactical issue illustrated by the situation above, that of an epistemological obstacle. Some mistakes that students make are simply results of random misunderstandings or misreadings. Others, on the other hand, appear with sufficient predictability, and despite a sufficiently wide variety of teaching approaches, that they need to be recognized as arising from something more serious than random miscalculation. One, for instance, is the pervasive notion (commonly known as the Freshman Rule) that if the need is great enough, then f(a+b) = f(a) + f(b). Another is the failure to take sufficiently seriously the difference between finite and infinite reasoning. There are many others. Like the didactical transposition, they are not an avoidable phenomenon. In this case, the inevitability is wound up in the fact that for its initial learning, a topic must be simplified-often in some sense oversimplified, leading to some impressions which are false, but are a necessity en route to more complete and sophisticated knowledge.

It should not be assumed that any student error with a particularly high nuisance value is an epistemological error. Duroux¸ gives a list of the defining characteristics of an obstacle: a) It is a piece of knowledge or a conception, not simply a difficulty or lack of knowledge; b) This piece of knowledge produces answers which are correct in some frequently encountered context; c) But it generates false answers outside of this context. A correct and universal response requires a notably different point of view; d) In addition, this piece of knowledge withstands being confronted by contradictions and resists being replaced by a better knowledge. Possession of a better piece of knowledge does not suffice to make the original one disappear ... It is therefore indispensable to identify it and incorporate its rejection into new knowing; e) After it is known to be inexact it still continues to show up unexpectedly at odd times. [Duroux (1982)]

Such are epistemological obstacles, and they provide a rich and valuable area of study. This study originated with Bachelard in the 1930's, and has beed pursued in works by Brousseau himself, as well as those of Salin (1976), Cornu (1983) and others.

The measurability debate thus clearly illustrates a solid attack on an epistemological obstacle. The topic in question could be disposed of in a snappy five minutes by the simple presentation of a couple of examples and a statement that it is thus clearly necessary to be on the alert when dealing with the infinite. But equally clearly, this snappy presentation would have far less chance of having a lasting impact on the students' mental model than the cumbersome, risky (it could easily have taken another three circuits before settling down) process of debate. Furthermore, the shared process of getting in and out of muddles is exactly the model of the scientific process for which Legrand so feelingly pleads. As such, it is a highly desirable state of affairs to obtain.

There remains then one large and highly relevant question: how does one achieve such a debate? The answer has many facets, but a key one is the recognition that what is involved is a major restructuring of the didactical contract. This is another of Didactique's foundational objects of study. Loosely, it is the underlying contract which governs the workings of the classroom, and in particular the relationship between teacher and student. It is in general almost entirely implicit, and is recognized by the furor, protest or simply discomfort created when it is broken.

For most students, after twelve years in the educational system, one firmly imbedded element of the contract is that the teacher will supply instructions of a sufficiently clear and thorough nature that a student who conscientiously follows them will be saved the embarrassment of making many errors. The corresponding contract element for the teacher is that a student who is informed that she has made an error will make all due haste to cover it up and see to it, by whatever means necessary, that she does not repeat it. These are among the many elements of the didactical contract with which there must be an absolute rupture before Scientific Debate can take place. Unfortunately, since the didactical contract derives a lot of its impact from the fact that it is implicit, one cannot simply walk in and announce a new contract. Legrand's solution is to make the rupture itself explicit by giving his students very clear advance notice of what they should expect and why. Thereafter a new contract presumably grows around the framework he has explicitly provided. Note the "presumably"-this situation has enough of the human factor to make it impossible to guarantee the desired social response, or even that the desired social response will have the expected mathematical consequences. (see for instance Balacheff, (1992))

Legrand describes his introduction as follows:

Since they do not correspond to the standard practices in a lecture course, the practices of the debate need, we feel, to be explicitly established at the beginning and to be regularly discussed with the students with regard to their epistemological and didactical significance.

The following aspects in particular need discussing:

-The fact that something is said or written does not constitute an institutional validation of its truth, usefulness or adequacy, because the teacher, wheh he cooperates by saying something louder and/or by writing it on the board, is not engaging his professional expertise in this phase of the spadework; on the contrary, he invites the other participants to take a position on the assertions by the device of taking an indicative vote, whose approximate results he explicitly writes on the board, and he invites personal involvement by oral explanations and judgments on those explanations.

- The debate does not, thus, consist of pitting one opinion against another, nor of hitting out and then awaiting the arbitration of the teacher (who, by definition, is right). Instead, for it to function everybody must produce arguments based on facts which are known to everybody else, or which come from the collection of common references (axioms or previously admitted or proved theorems.)

-The arguments thus developed (proofs and verifications) have as their objective the explanation of what one has stated, or the demonstration of the truth or falsehood of general statements which certain protagonists have considered "sufficiently true" to be candidates for general discussion (conjectures.)

-At the end of the debate, it is a question of accepting these conjectures because they are thought to be flawless generalities (in which case they are declared theorems of the course, and are added to the common references) or on the contrary of rejecting them because they have been shown false by the production on the spot of counterexamples (they then become false statements to beware of, because if they have been proposed, they have some aspect that makes them seem deceptively true.)

-In every case, the goal of the debate is the discovery of solutions to problems, the verification of the accuracy of facts and general ideas, and the increased awareness of the benefits and limits of certain methods, and not the adherence to particular beliefs, people or groups. Needless to say, the debate is not used for any individual assessment whatsoever by the professor.

-Under this arrangement, argumentation and mathematical proof are the functioning medium by which the mini-community of the class grasps new objects, explains to itself what it believes itself to understand and persuades itself that it is not in error. [Legrand (1990)]

What are the end results of all this? That's not an easy question to answer either for the Scientific Debate or for the Didactique. The former has certainly proved to be reproducible-several people other than Legrand have taught it. Registration anomalies make it difficult to determine the long-range impact on the students' academic careers. Even if that could be determined, it would in some ways beg the issue, since even more than producing academically successful students, he wishes for the course to produce human beings with the capacity to use their brains and knowledge in a way that will improve their lives and the world around them. Measuring that is not an option!

As far as Didactique goes, rather than the end results, one should speak of the current results (which are many) and the end goals, because the field is so much alive, thriving and growing. It faces the challenges of any live research field-diversification without splintering; internal and external communications-and it is meeting them.

One thing seems very clear though. Both the existence of the Calculus by Scientific Debate and the strength of Didactique give clear evidence of a concern shared by many in this country. It was expressed particularly articulately by William Thurston:

"[often in classrooms] we go through the motions of saying for the record what we think students "ought" to learn, while the students are trying to grapple with the more fundamental issues of learning our languages and guessing at our mental models. Books compensate by giving samples of how to solve every type of homework problem. Professors compensate by giving homework and tests that are much easier than the material "covered" in the course, and then grading the homework and tests on a scale that requires little understanding. We assume that the problem is with the students rather than with communication: that the students just don't have what it takes, or else just don't care." [Thurston (1994)]

and that

"We mathematicians need to put far greater effort into communicating mathematical ideas. To accomplish this, we need to pay more attention to communicating not just our definitions, theorems and proofs, but also our ways of thinking. We need to appreciate the value of different ways of thinking about the same mathematical structure." [ibid]

This is not a state of affairs which is going to resolve itself overnight, but if we in the U.S. are planning to take it seriously, we would do well to keep our eyes on what is been done about the situation on the other side of the Atlantic.

BIBLIOGRAPHY

Balacheff, N.: 1991, 'Benefits and limits of social interaction: The case of teaching mathematical proof', in Bishop, A., Mellin-Olsen, S., and Van Dormelen, J. (eds.), Mathematical Knowledge: its Growth through Teaching, Kluwer, Dordrecht, 1992.

Guy Brousseau, Theory of Didactical Situations, Didactique des Mathématiques, 1970-1990. Ed. Balacheff,N., Cooper,M., Sutherland,R., and Warfield, V. Kluwer Press (in press)

Chevellard, Y. and Johsua, M-A., (1982)."Un exemple d'analyse de la transposition didactique", Recherches en Didactique des Mathématiques, Vol.3, number 1, pp. 159-239.

Cornu, B. (1983) : apprentissage de la notion de limite: conceptions et obstacles. Thése de 3eme cycle, Mathématiques, Université I de Grenoble.

Duroux, A. (1982) : la valeur absolue: difficultés majeures pour une notion mineure. DEA de Didactique des Mathématiques, Université de Bordeaux. Pubblished in Petit x, n^o 3, 1983, Ed IREM de Grenoble.

Legrand, M.:(1990).Débat scientifique en cours de mathématiques. Repères IREM 10. Topiques Editions

Legrand, M.:(1995). Mathématiques, mythe ou réalité, un point de vue éthique sur l'enseignement scientifique. Repères IREM n^o 20 & 21. Topiques Editions

Legrand, M.:(1995). Didactique et Enseignement (notes for a talk)

Salin, M.H. (1976): le rôle de l'erreure dans l'apprentissage des mathématiques à l'école premaire. DEA de Didactique des Mathématiques , Université de Bordeaux.

Thurston, W. (1994 ) On Proof and Progress in Mathematics, Bulletin, AMS, vol 30, number 2, April 1994, p. 166-8