Figure 1
Article for the Mexican Journal of Educational Science
(Congress of Aguas Calientes, Mexico)
Education and Didactique of Mathematics
Guy BROUSSEAU
Professor Emeritus, IUFM of Aquitaine
October, 1999
Introduction
As the 21st century begins, we are approaching mathematics education using means of a totally different measure from those used in the past. Nonetheless, it is not clear that in these new circumstances our knowledge and our practices insure us today a better regulation and effectiveness than at the beginning of the 20th century.
We are still asking ourselves what contributions from mathematics are "necessary" to education and society, and how to bring about those contributions; articles on the objectives of the teaching of mathematics abound. They explain the necessity for a society to have available simultaneously a sufficient mathematical culture for each citizen and also the number of technicians and savants it needs to face the demands of the future. All the indications are that mathematics will play an important role in that future. These articles explain also the importance of the educational properties proper to mathematics, both at the individual level for the capacities it seems to develop and at the level of collective life. The domain of mathematics is where the child can have her earliest initiation into rationality and forge her first reasoning ability in autonomous and social relations.
Today we are inquiring as well into the means we have created to respond to the question: to what degree does the success of the diffusion of mathematical knowledge depend on the Science of Education, or on mathematicians themselves, or what place has the knowledge of didactique, or more particularly didactique of mathematics in this diffusion, what institutions can insure the coherence and pertinence of this type of knowledge?
I am not it a position, and it is not my business, to set up a general table of the state of mathematics education throughout the world and make an inventory of the trends which are visible as the century ends. The quantity and quality of experimental works, the multiplicity and diversity of didactical propositions at the end of this century exceed the bounds of this conference and probably my capacities to inform and synthesize.
Rather than a vast panorama, I will therefore offer you a visit to these questions following a route which I know well because I followed it. I will restrict myself
This approach, the Theory of Didactical Situations, is present today as a scientific instrument. It tends to unify and integrate the contributions of other disciplines and it gives a better comprehension of the possibilities of ameliorating and regulating the teaching of mathematics.
But it is not my intention to proselytize a new teaching method, even though numerous applications have resulted from this approach. It seems to me that 20th century education has had no shortage of prophets and innovators. My hope is simply to contribute to your reflections on the relationship between the "content" of teaching and the methods of education.
The origins of the Theory of Situations
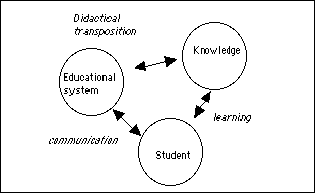
One of the standard ways to envisage teaching is as the relationship which deals with the transmission of a given piece of knowledge between the educational system and the student, and likewise to regard the didactical relationship as a communication of information.

Figure 1
This three-way schema is habitually associated with a conception of teaching in which the teacher organizes the knowledge to be taught into a sequence of messages from which the student extracts what he needs. It facilitates the determination of the objects to be studied, the role of the actors, and the division of the study of teaching among sundry disciplines. For example, mathematics is responsible for the content, the science of communication for the translation into appropriate messages, pedagogy and cognitive psychology for understanding and organizing the acquisitions and learnings of the student. The goal of these messages is essentially the acculturation of the student by society. To be sure, this schema does not exclude the complementary intervention of other disciplines, to clarify this or that aspect of the process, but it gives a hierarchy for their impact.
A propos of learning phenomena, psychologists have never ceased showing the importance of the natural tendencies of subjects to adapt to their environment. Not only SKINNER (role of stimuli), but also PIAGET (role of personal experiences in the spontaneous development of fundamental schemes) and VIGOTSKI (role of the socio-cultural milieu.)
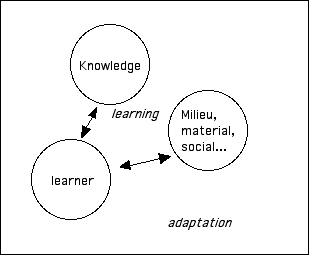
Figure 2
Thus, for example, even though he works in an essential way with the non-scholarly genesis of knowledge, PIAGET in many cases refuses this duality in order to coordinate it (apriorism and empiricism into reflective abstraction, assimilation and accommodation into equilibration, etc.)
In this perspective, education becomes an activity which can only conciliate two processes, one of them that of acculturation, the other of independent adaptation.
Identifying the knowledge developed by the subject in contact with the milieu with the knowings taught, and identifying the learning with the student produces a four-way schema:
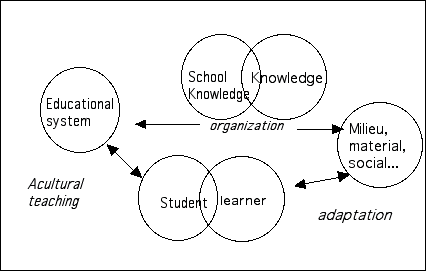
Figure 3
Since the beginning of the century, the works of psychologists have continuously influenced teaching. But their results only appear as means of "fixing" it. They are supposed to be taken into account by teachers without anyone knowing how to do so. Recent injunctions like "the child should be placed at the center of the preoccupations of the educator" demonstrate a desire to react against the logic of communication but do not hide effectively the inability of psychology and pedagogy to intervene in any way except to criticize and correct. Hence these efforts don't succeed in modifying the three-way scheme noticeably.
But in the 60s, the environment of the student was not in itself an object of study. What people were trying to model was the learner, the process of producing or learning knowledge or the structure of knowings. For SKINNER the black box was the subject, the stimuli were decidable by the experimenter, thus "known", or more precisely transparent and it was convenient to model the subject. Piaget's scientific culture furnished him with all the knowledge he needed to conceive of experiments in which the child revealed his modes of thinking, and to recognize in his behavior the mathematical structure and knowledge of his choice. A fortiori, although the modalities of the influence of the socio-cultural milieu on children's learning were taken into account and studied by VYGOTSKI, the study of the milieu itself arises in a completely different field, ideological or scientific.
In the 60s, while I was still a student of mathematics and also studying cognitive psychology with Pierre GRECO, I was impressed by his cleverness in conceiving experiments arranged to expose the originality of children's mathematical thinking and the stages in their development. But I noted that he made no effort to analyze the design of the experiments that he invented and to make explicit the relationship between this design and the mathematical notion whose acquisition was being studied. In fact, when PIAGET used the PEANO axioms to identify THE development of THE knowledge of THE numbers in THE child, it seemed to me more like interesting but risky wagers than like evidence. I could produce "definitions" of the natural numbers, mathematically equivalent to the PEANO axioms, but of very diverse cognitive complexity. Mathematical equivalence does not imply cognitive equivalence. In fact, producing a tiny variation in the numbers proposed was enough to see that the knowledge of THE numbers was actually that of some numbers. What permits us to state that it is exactly this mathematical knowledge which is the subject's knowledge, and not some other, more general or more specific? These observations were not objections to the work of PIAGET, but to the overly precise use people made of it to talk about the acquisitions of a particular child in a particular situation and infer didactical prescriptions.
It therefore seemed to me that this work needed to be extended to the study of the experiments themselves and their relationship to this or that knowledge: in what conditions could a subject — any subject — be induced to need this knowledge in order to make decisions, and why, a priori would he do it? Without Piaget's experiments, this idea would have been trite, because studying the problems and exercises that make use of a particular mathematical notion is a customary work of mathematicians. But since every notion calls up a whole set of problems and exercises, it looked as if this line of research had almost no chance of producing any information about the acquisition of knowledge that had any generality. In this perspective, the children's behaviors are what reveals the functioning of the milieu considered as a system: the black box is thus the system.
At that period, teachers of mathematics were trying to invent exercises to accompany the introduction of new mathematical knowledge, and in my eyes their effort betrayed a certain poverty of our didactical conceptions. Most often they contented themselves with finding an example in which a simple translation made it possible to "read" the elements of the structure, or the properties announced in the definition, or the mathematical theorem. The application in the literal sense of mathematical structures to a wide variety of objects and relations was interesting, but it confined the student to the role of spectator and the teacher to the role of stage director. At best, making the student take action consisted of communicating to her the conditions and properties of a generating system and having her produce the intended knowledge (formulas, declarations, etc.) by exercising rules which had been taught her, as proposed by Z.DIENES. In these conditions, the question which, repeated for every proposition envisaged, engendered the work we are going to talk about was "Why?": why should a subject do this rather than that? Why does this knowledge demand that behavior?
This attitude leads naturally to considering a problem or exercise not as a simply re-formulation of a knowing, but as a device, as a milieu which "responds" to the subject according to some rules. What game should a subject play in order to have a need for this particular knowledge? What adventure — succession of games — could lead him to conceive of it or adopt it? In this approach, the subject need not be any better described than a checkers player, who plays the white or the black following an impersonal strategy. What information, what pertinent penalty should the subject receive from the milieu to orient her choices and take on this knowledge rather than that one?
The same approach then leads to considering the milieu as an autonomous system, antagonistic to the subject, and it this milieu which it is convenient to model as a specific mathematical game for which the given knowledge would be the means of determining the minimal winning strategy. The pair formed by a game and a strategy (winningor not) becomes a sort of mathematical automat whose properties can be studied.
We gave the name "situation" to a model of the interaction of a subject with a certain milieu which determines a given knowledge as the means, for the subject, of obtaining or conserving a favorable state in this milieu. Some of these "situations" require an "anterior" acquisition of all the necessary knowledge and frameworks, but others offer the subject the possibility of herself constructing a new knowledge in a "genetic" process, that is, one which engenders it.
Choosing to take the conditions in which knowledge appears as a system and not as an undetermined collection of variables acting independently of each other is a fundamental characteristic of the Theory of Situations and its methods. The obligation always to define the objects being studied -- for instance a piece of mathematical knowledge -- by their function in a system appears to restrict the means of explanation. But in fact it is a magnificent sourse of relevant questions and verifications of the consistency of the means of analyzing the fact of teaching.
Note that the same word "situation" serves, in its ordinary meaning, to describe not only the set (not necessarily determined) of conditions surrounding an action, but also the theoretical and possibly formal model used to study it.
In 1970 the scientific project was proposed: it consisted of modeling (and criticizing) the situations used to introduce or teach mathematical notions and imagining other more appropriate ones. Posing the problems in this way, side by side with arguments about the logico-mathematical organization of knowing, makes it possible to introduce into the analysis, or even the calculation, arguments of an economic and ergonomic type. But it is also possible to take into account other constraints, in particular those which might appear at the conclusion of works of psychology or sociology, on the conditions for making them functional, that is, of clarifying how they might intervene effectively.
An example of the application of this methodological principle would perhaps be welcome. We shall supply one in the next section of the article, in the domain of the teaching of number.
It would be pointless to indicate here all the conditions which resulted in this idea of the student becoming a working hypothesis and a method and a research program for a whole generation of researchers in mathematical didactique in France. The project and the program of IREMs and the regulation of the reforms of the 70s are at the center of these events. It was apparent even at that period that searching for the conditions for the existence of a knowing is a general means of research and engineering in didactique. The systematic description of didactical situations is a more direct means of discussing with teachers what they are doing or what they could be doing and of considering a practical means for them to take into account the results of research in other domains. A theory of situations thus appeared as a privileged means not only of understanding what teachers and students are doing, but also of producing problems or exercises adapted to knowledge and to students, and finally a means of communication between researchers and with teachers.
An example: natural numbers
Two classic situations
Let us begin by describing two culturally classical situations used to see if a child knows how to count.
A popular practice: Baby is counting, family scene
Mother: Guess what, Grandpa! The little one knows how to count!
Grandpa: Really? Show me, sweetie..
Mother: Show Grandpa that you know how to count
Child, (age four): One, two,three,four,five,six,seven,eight,ten,fifteen,uh…
Grandpa, full of admiration: Very good! Now all you need is to keep going!
A professional practice: "Counting" that way doesn't count
But the family also includes Aunt Mimi, who is a retired elementary school teacher.
Aunt Mimi: No, no, Grandpa, that's not what it means to know how to count: to know whether the kid can count you have to show him some fingers and ask him how many they are, and then make him show the same number of his own fingers! It's not enough to be able to say the numbers in order! And if he doesn't succeed, there's no reason for Mama to be disappointed. At age four most children barely really understand numbers bigger than five, that's what the psychologists say.
Mother: But little Odile next door is just five and she counts all the way to seventy!
Aunt Mimi: Yes, and she can also recite the pledge of allegiance which has more than 70 words, but she thinks forwhichitstands is all one word. It's not all that bad, but one of my young colleagues says parents these days are really pushing to make their kids "count" super-young. She says that one result of this pressure is that some of her students start counting the minute they hear the word "number" without stopping to listen to the question they're being asked. She has a pre-school class with some children who count mechanically up beyond fifty and as a result she can't organize any mathematical activity that's appropriate to their age and works both for them and their classmates who can't get past five.
Analysis and modeling
The model of the second example clearly includes and corrects the former. In both cases the formulation of the numbers is indeed an appropriate response to the question, but Aunt Mimi modifies the initial model {teacher, student, knowledge} in an essential way by substituting for it the model {teacher, student, knowledge, milieu} where an objective milieu is the number of fingers to count or show. Thus, in his relationship to the milieu the child must restrict his response to a new form of validity which is not just that of acquiescing to the desire of an adult.
This restriction obviously gives a completely different meaning to knowledge, which becomes the adequate means of responding to the necessities of an objective situation, denuded in itself of didactic intentionality. But note that the child has no means of understanding the question "How many?" nor of responding unless he has previously learned the meaning. In addition, he has no means of verifying for himself the validity of his answer. The judgment of his correctness remains in the control of the teacher. This situation is thus essentially a situation of evaluation of knowledge.
It can only be used for teaching in the framework of a behaviorist didactique consisting of repeating questions, teaching how to establish the answer and, here, of having the child reproduce the techniques of counting in direct question-response association, to the point of perfect reproduction.
On this subject, in one of his most famous experiments, PIAGET asks young children: "Where are there more sticks?", showing them two collections with the same number of sticks, one more spread out that the other. For beginners, this always produces the same criticism: the question is ambiguous. It is necessary to know about numbers to understand that it is a question of number and not place occupied. And in fact, questions of evaluation always have the property that you have to know the answer in order to understand the question.
In a "learning" situation in which the student is supposed to "adapt himself to an objective situation" (and not to a "dual" relationship with the teacher) by himself producing the knowledge in question, it is necessary that the assignment or the project of the action be able to be conceived of by the subject without the help of its solution because that's what is supposed to be constructed or acquired. To understand the situation, the student needs to be able to envisage, with his current knowledge, a basic strategy which corresponds to the assignment which has been given him. The new knowledge is then the means of producing the expected effect by a strategy which is more efficient, surer, more economical, etc. The pieces of knowledge are in competition and the motives for learning are "economic" laws which manifest themselves to the student himself.
"Behaviorist" teaching calls for a meaning, but that meaning is outside of the process of adaptation. It follows that it is the teacher who should decide what she is going to consider to be elementary teaching. If the knowledge is too complex, she will have to take it apart, teach the parts, and then teach the composition of these parts. The reasonings for this decomposition are beyond the student's understanding and the meaning of what he has learned cannot be given him until after the fact, by its use. Which explains the necessity for giving a high multiplicity of exercises applying the piece of knowledge learned. The meaning of this piece of knowledge will be represented, not by its usefulness in establishing answers, but by a universe of situations determined by their analogies. Thus, the classical teaching of division separates the teaching of the algorithm and that of its meaning.
We will not pursue this analysis, the point of which was to model how an interpretation of practices operates, in terms of restriction of the student to a situation.
Hypothesis of the fundamental situation.
The empirical course of action consists of trying to improve these practices. We will rather follow the other course, which, starting from a particular piece of knowledge, seeks out types of situations which will cause it to appear, cause it to be used, cause it to be constructed and cause it to be learned.
For heuristic reasons, we assume that every piece of mathematical knowledge possesses at least one situation which characterizes it and differentiates it from all others.
In addition, we conjecture that the set of situations which characterize the same notion has a structure and that it can be generated by a small number of situations which we will call fundamental, by the play of variants, of variables and of bounds on these variables.
But before attacking these theoretical questions, it seems to me useful to give a concrete illustration of the notion of fundamental situation by presenting the one which corresponds to natural numbers. We will not go into the reasoning about the didactical engineering which goes beyond what we are about to give and by which we arrived at this result, nor the arguments which militate in favor of the idea that this situation is reasonably close to the fundamental situation.
It is interesting in any case to remark that rather than blindly criticizing practical situations, it is more effective to compare them with a fundamental situation.
Before we give this example, it is important to reiterate for an instant that a fundamental situation is not a priori an "ideal" situation for teaching, nor even a more effective one. The value of a situation for didactical use increases as a function of a large number of other external parameters such as the effective possibility of putting it to work in a given psycho-socio-cultural environment.
The fundamental situation of counting
To satisfy the above conditions, and using various conclusions from the theory, we obtain the following situation, which can be translated into instructions appropriate for children of age 3 to 7:
"We have paint in these little pots. You need to go get some paint brushes over there and put one in each pot. You need to bring all the brushes at once and there has to be a brush in every pot and a pot for every brush. If it doesn't come out right, you have to take all the brushes back and try again. You will know how to count when you can do it even if there are lots of pots and brushes."
This situation includes the preceding one, in the sense that as soon as the number of pots gets large enough, the student either must have material means of representing the collection (drawing, enumerating with her fingers or otherwise, etc.) or must count it, if necessary by organizing her enumeration. The numbers are no longer the explicit object of the question, but rather the implicit means of responding to it.
To have the number appear explicitly, it is necessary to transform this auto-communication into a real communication:
"You are to stay close to the pots and say or write a message so that your classmate can bring you the number of brushes you need. If she brings you too many brushes or not enough then you both lose. You will know how to count when you can do it even if there are lots of pots and brushes."
The child will know how to enumerate when he can play both roles: ask (transmitter) someone (receiver), orally or in writing, for the right number of brushes and check the operation, and inversely furnish on request the desired quantity.
The means of resolving this problem will evolve, in particular with the sizes of the collections and the forms in which they are presented. The knowledge of small numbers will be enriched when they serve to construct others with the aid of various operations. It must be observed that the children rapidly acquire certain real schemes which are true for any number, but also that the effective possibility of taking these schemes as objects of knowledge and handling them as knowings is not acquired either spontaneously or rapidly. Sooner or later it is necessary not to content oneself with their use, but also to elucidate, formulate, discuss numerical properties and structures. These elucidations are necessary to the learning itself and must accompany it. How and when? Knowledge of THE numbers is not reducible to that of the PEANO axioms. Human knowledge is not contained in the knowings which summarize it.
The difference between counting as a customary cultural knowing and counting as knowledge of a means of resolving the fundamental situation is visible in the following example due to B. VILLEGAS.
The meaning of enumerations
The preceding situation is proposed to some children in the midst of (classical) learning who already "know" how to count in the sense that they know how to resolve the problem of the transmitter and that of the receiver (say, to thirty), but they haven't yet mastered enumeration. One can then observe at times the following behavior:
The student goes to get a bunch of brushes and distributes them amongst the pots.
-"Oh, there are three left."
-"Did you succeed?"
-"No, because I have three left!"
-"OK, take them all back and try again"
The other students in the class suggest:
-"Count, count!"
The student counts the pots, leaves, grabs a handful of brushes and returns. Counting hasn't done a thing for him. The other students continue to help him:
-"No,no, you have to count the brushes."
The child leaves, counts all the brushes, takes a few of them and returns…
A supplementary condition: confidence in one's methods
Can we affirm that the student knows how to count when she is able to put together correct collections of no matter what size in the conditions of the fundamental situation?
Not altogether: she also needs to be capable of being sure enough of her count to identify the source of errors and if necessary discuss them.
For example, if at the moment that she goes to look for the brushes somebody snatches a pot, she needs to be able to understand and say "You cheated!"
This confidence in her method in turn requires a reflective position with respect to them, "metacognition" of the words to express the knowledge acquired, a metalanguage and everything that constitutes the conversion into know-how of certain parts of the knowledge. Thus our situation of enumeration was not altogether fundamental. Is it now?
`With regard to classical methods, this fundamental situation of enumeration could turn out to be useful at various moments of the teaching and especially to indicate to teachers what "counting" means in "concrete" terms. That does not mean that learning exclusively by means of the fundamental situation would be more rapid or more effective. It could turn out to be uselessly heavy once the student has understood the goal of the teaching.
The organization of the long genetic processes
How is the acquisition of a complex mathematical structure like that of the natural numbers organized? Clearly it necessitates long processes. How is the first knowledge acquired articulated with that acquired later?
Learning the partial practices of counting separately requires that the adult teach them, require them, correct them, have them imitated and repeated and then compose them. At no time is the child in a position to establish the final result of the action for himself and correct his own errors. Nonetheless, parents and teachers use all these degenerate forms of the fundamental situation with a certain measure of success, even the extreme case of the formal teaching of the sequence of numbers. So it is not a matter of rejecting some of them, but of using them to their best according to their particular characteristics.
The principal disadvantages of "partial" learnings are the following:
-they do not make it possible to defer to the child the responsibility of judging the value of her answers, nor to describe to her in advance a learning project of which she can evaluate the progress
-she has to have learned the answer in one way or another in order to understand what is being asked of her.
The Theory of Situations makes it possible to study existing solutions and to propose different ones, in particular, replacing partial techniques with an intelligible global genesis. The presentation of such a genesis is beyond the scope of this article, but the use of the fundamental situation and of the pursuit of the knowledge of larger and larger numbers plays an essential role in it.
Learning numbers
This example leaves in the shadows the diversity of situations necessary for the whole of the process, the complexity of the relationships with knowing, and a great many phenomena which will no doubt be worked on in workshops at this conference. Because in the end, what is necessary is for the child to enumerate the collections (in the sense of listing all of the elements one after another without repeating any) at the same time as evaluating their size (in the sense of evaluating their cardinality in correspondence with another collection), in particular when he counts them (in the sense of setting up a correspondence between the elements and the words) then, if the counting has been decomposed, by "numbering" (by expressing the number orally using a system of numeration) the result of his counting and then by writing that number. He also must appropriate the ordinal uses or the sequence of numbers, etc. The denomination and writing of the first numbers use procedures of numeration which must be recognized to be used, but whose study and analysis must continue throughout school if only to recognize and use new numbers. The analysis of numerical encrypting and of systems of numeration as opposed to the practice of the numeral, notably the reading of numbers, is indispensable.
Reasoned uses of fundamental situations
But this learning could be produced by a conjunction of methods: for example in a constructivist process, by completing the spontaneous or provoked responses and (indispensably) institutionalizing them. Or in more classical, Socratic or even axiomatic teaching, with lessons followed by exercises in response to a problem well identified henceforth by the student.
Likewise, the fundamental situation does not discredit any of the forms of learning. It permits all of them and makes it possible to combine them: it completes the partial learnings which remain useful and no doubt necessary, and above all gives them their meaning.
3. Some elements of the Theory of Situations
The search for and invention of situations characteristic of a variety of pieces of the mathematical knowledge taught in schools, the study and classification of their variations, the determination of their affect on the conceptions of the students, and the segmentation of notions and their organization into long teaching processes constitute the material of mathematical didactique and the terrain in which the Theory of Situations furnishes concepts and methods of study. For teachers as for students, the presentation of the results of these works renovates the knowledge and the ideas they have of mathematics, and this even if they have to develop a whole new vocabulary to establish the relationships which connect the conditions of emergence and teaching of basic mathematical notions with the expression of these notions in the classical mathematical culture. We will not continue in this direction here, because it would take too long to present the contributions of the Theory of Situations to the teaching of different mathematical notions such as natural numbers, rationals and decimals, space and geometry, beginning algebra, statistics and probability or reasoning and logic. It is important to note that the concepts we propose to advance are very general and can appear be exportable for the study of other subjects of teaching in other disciplines, but in science one must always distrust analogies. In the same way that there is no metaphysics which will simultaneously generate thermodynamics, optics and electricity, what I am about to present constitutes a sort of metadidactique which is not automatically convertible to treat whatever knowledge comes to hand.
The structure of situations
General model of a situation
A situation models the relationships and interactions of one or more actors with a milieu (an environment). The model consists of
-a representation of the states of the milieu, and the changes which the actors can produce in it
-the goal of the action, generally an end state of the milieu and the benefit attached to it for the actor
-and the inventory of the choices permitted by a set of rules.
A piece of knowledge is pertinent in this situation if it is the means of mobilizing a strategy or a tactic within the framework of the choices permitted at each instant. Among the pertinent pieces of knowledge – ones that determine some choices – some are adequate: they make it possible to achieve the desired end state, and among these some are more efficient, more dependable or more economical than others.
This model makes it possible to identify the knowledge of a subject, or at least the part that her behavior reveals: it is a question of looking for the "simplest"" knowledge which would generate the "simplest"" strategy which coincides with the decisioins observed. It then makes it possible to compare it with other pertinent knowledge, in particular with the optimal knowledge in this situation. It is thus that we showed the importance of the procedures and knowledge of enumeration – independently of counting – in the learning of numbers and their operations.
For simplicity, let us return to our schematization of the situation by a triple: {actor, rules of interactions with the milieu, knowledge}.
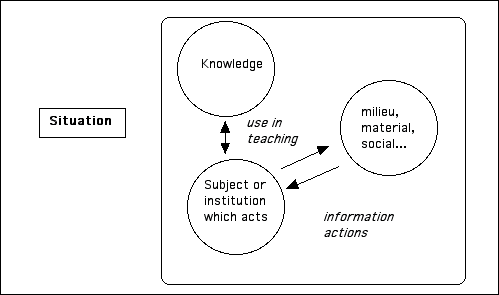
Figure 4
This model is the one generally adopted to conceive of a general finalized activity in a general institution. The actor himself can be an institution.
When is one situation a realization of another? When are two situations different? The definition of general instruments of comparison of situations is still quite uncertain, especially on issues of hierarchy and the collecting of situations and associated knlowledge. The whole goal of the Theory of Situations is to make possible a local organization of elementary knowledge according to its level of appropriacy to the circumstances and possibilities of the subject, and at the same time to make possible its reorganization according to the logical and theoretical necessities which are the fruit of a quite different adaptation by society.
Interactions
Anthropological observations as well as the logic of the methodological principles of the Theory of Situations lead us to distinguish three fundamental types of interactions of an actor with the milieu:
- "action"" , which consists for the actor of fixing a state of the milieu or of determining or limiting the actions of the other actors (materially or by imposed rules),(Figure 4)
- "communication"" , which consists of modifying the knowledge of another actor by means of messages carrying information,
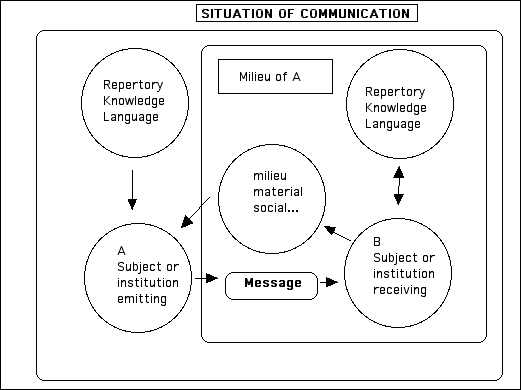
Figure 5
- "proof"" , which deals with justification or cultural validation of acts or statements.
Each of these interactions is modeled by various types of situations and mobilizes various repertories of means.
For example, it is easy to show why "give a proof"" appears in a very different situation from a simple communication of information: the structure of the situation, that is, the position of the actors with respect to the milieu, is very different, as are also the game, the rules and the reportory of means of proof.
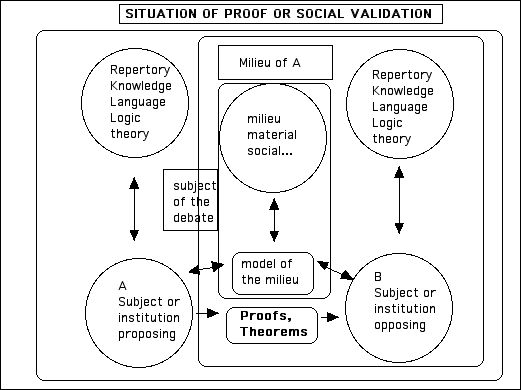
Figure 6
In class, this classification of situations has favored the installation and observation of the passage from situations of argument to situations of proof. Without it the initiation into these practises is not easy to accomplish.
These situations are not only an important step in the mathematical process, they also bear the responsibility for an essential educational project: that of turning the student into a rational, socially autonomous and responsible being, capable of understanding how a truth is established and shared in a society, by debates which are both democratic and constructive.
The two meanings of "didactical situation""
The term "didactical situation" currently has in fact at least two meanings:
Certain situations with a didactical use have the property of permitting the student to make pertinent decisions on his own, to judge their effectiveness and to adapt himself to the milieu by the construction of the desired knowledge. These situations have a "non-didactical" model in the sense that they do not require a specific didactical intervention (other than devolution). Contrasting with to this limiting case are the purely didactical situations where the teacher has to intervene at every moment in the development of the student’s activity to provoke it, orient it, restrain it and control it according to his own didactical strategy. In general, real teaching situations can be separated into a didactical component and a non-didactical component (dedidactified) which can occur simultaneously or successively.
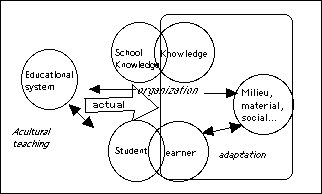
Figure 7
Consequences; demonstration of various phenomena
Types of consequences
A scientific theory is, formally, a collection of "true" statements. Its principal use is to derive or discard declarations with certainty starting with those already known, but even more importantly to produce new arguable conjectures. These conjectures need to be reasonably and have as many concrete consequences as possible. The theory should above all give the means and methods for deciding on the truth of the conjectures. Originally the only objective of the Theory of Situations was to verify the consistency and feasibility of the didactical injunctions and objurgations addressed to the teachers by their counselors and decision-makers. It gave rise to a long comparison which is far from being over. But it has become far richer and more complex. The effort to maintain the consistency of the set of declarations which are expressed with its concepts is becoming heavy-duty. It is becoming difficult to apprehend and to teach to young researchers, and especially to teachers.
The approach to teaching by the Theory of Situations has produced numerous results
But its principal consequences are probably epistemological ones. We shall now examine certain of those.
Conceptions and obstacles
We have been reasoning as if one could habitually isolate a piece of knowledge, and as if knowledge and situations were easily isolatable entities. In fact, an actual milieu puts together families of situations which mobilize knowledge structured by logical relations, relations of convenience, frequent co-presences, etc.
Pieces of knowledge function as aggregates which we call "conceptions" and likewise situations group themselves into "milieus".
"Milieus" and groups of situations — such as those of geometric figures drawn with ruler and compass — call forth aggregates of knowledge adequate for being structured into mathematical theories — in this case, Euclidean geometry. In the same way that pieces of knowledge group themselves around theories and concepts in the knowledge of scholarly institutions, pieces of student knowledge group themselves into "conceptions" which characterize a certain manner of understanding and using a mathematical notion in a certain field of situations.
The study of the forms of "dependence" which connect these pieces of knowledge, that of theoretical processes of aggregation and that of experimental modes of making conceptions evident has been going on for twenty-five years and is continued today in the study of ecosystems and praxeologies in the anthropological approach.
The situations about a new piece of knowledge encountered by a beginner are necessarily small in number and often simplified. Adapting knowledge to this limited milieu leads the student, but also the teacher, to use conceptions which will turn out to be ill-adapted, approximate or even false in situations encountered later on. These initial conceptions are not errors or faults of comprehension on the part of the student, but are the inherent and inevitable result of a well-adapted teaching. Recognition of this fact completely changes the problematique of the long term organization of learning as well as that of the review of old knowledge in a teaching process.
In addition, it has been shown that this initial knowledge could organize itself into obstacles in Bachelard’s sense of the term, even in mathematics. For example, as we indicated above, primary school knowledge of natural numbers can be an obstacle to the comprehension of rationals. It’s not a matter of difficulties, but of actual knowledge, initially necessary, but enduringly perturbing to later learning, and persisting even after the acquisition of correct knowing. Deduced a priori from the Theory of Situations, the fact has been observed in many examples.
The relativisation of knowledge
The definition of knowledge by its function in a situation carries with it the fact that for the same mathematical notion each actor (society, teacher, student) develops knowledge which a priori differs with the conditions in which she will use it, create it or learn it. Whether or not valid from an academic point of view, each is up to a point thus legitimized and recognized. A false idea appears and disappears according to the same laws which govern the appearance and disappearance of a valid idea. The fact that an observer knows that a piece of knowledge is false because it produces errors is not necessarily the mark of an erroneous functioning of the mechanisms of cognition of the observed subject. The Theory of Situations deals with the present and anterior conditions which "justify" the state of this knowledge and with the use which can be made of it.
For example, all students establish their understanding of the multiplication of two numbers by its meaning in the natural numbers: 5 x 4 represents 5 + 5 + 5 + 5, and they verify their results implicitly by "properties" like: "the product of two numbers can’t be smaller than the larger of the two numbers". When the day comes that they have to multiply 0.8 by 0.5, their means of comprehension and verification disappear. It’s a completely different operation, even though it has the same name and bears a little resemblance to the preceding one.
Inversely, the fact of according to a student or an institution the legitimacy of knowing a notion in some particular way doesn’t make this recognition an essential object in the work of the teacher. Amongst the erroneous pieces of knowledge, the only ones of interest are the ones that have meaning for other students, that is the ones which have a relatively large probability of being reproduced, and which can be explained and eradicated in a reasonable time, etc. These pieces of knowledge are not a priori degradations or errors with respect to culturally established knowledge. They have a legitimacy which needs to be understood and respected, even if one wishes to modify them.
"Relative" pieces of knowledge can be compared to "scientific" knowledge or "universal" academic knowledge. But one should be on guard against confusion: the fact of recognizing that these pieces of knowledge have a real existence, and thus a certain adequacy or a certain legitimacy doesn’t mean that they are "true" and especially not that they are "equivalent" to the others.
The gradient and the didactical transposition
With regard to the same notion, two institutions can have different knowledge. This can cause difficulties in their collaboration if they enter together into a new institution. Beyond a certain point, an effort at homogenization is necessary. It translates itself by a didactical situation: one of the institutions attempts, directly or with a third party mediating, to modify the repertoire of the other. Often the actual didactical action is reciprocal. The greater the size and number of these differences, the larger are the difficulties in cooperation. This kind of gradient thus creates a didactical pressure. On the other hand, teaching is only possible if the repertoires are not too different and it happens at the price of an adaptation — spontaneous or meditated — of the knowledge transmitted, called the didactical transposition. Furthermore, the very fact of teaching a piece of knowledge modifies it, both for the teacher and the taught. Transposition is a modification of knowledge which changes its role, the situation where it intervenes. It is a condition and an effect of the didactical relation.
Paradoxes of the didactical "contract"
Jeanine Filloux, extending the social contract of ROUSSEAU, came up with the notion of the pedagogical contract, in which one specifies with the students, with society and with teachers the reciprocal obligations of each with respect to the others. Can this contract be extended to the "teaching" domain of education? Can the teacher specify and pass a teaching contract in the same way? Early on, I imagined that a teacher acted on the system {student, situation, knowledge} in exactly the same way that a student acted in a non-didactical situation. In which case, the didactical contract would have been simply the rules of this situation. I came to realize that that model led to contradictions pointed up in reality by paradoxes: for example, the teacher cannot formulate in advance what the student will have to do in a problem without thereby depriving her of the possibility of manifesting or acquiring the corresponding knowledge. The teacher cannot engage in an attempt to make a student "understand" a piece of knowledge, much less produce it: nobody knows how one "makes" new mathematics, much less how one makes someone else do so in any guaranteed way. Which means that the didactical relationship cannot formally produce a contract; the clauses cannot be written; the sanctions resulting from a rupture cannot be provided, etc. But for all that, the illusion of a contract is indispensable in order for the relationship to be taken up and on occasion to succeed. Each one, the teacher and the student, has an idea of what the other expects of him, and of what each one thinks about what the other one thinks about him… and this idea creates the possibilities of intervention, of devolution of the a-didactic portion of the situations, and of institutionalization. It permits the fiction that the teacher teaches a definite knowledge preparing without side effects for further acquisitions. The Theory of Situations demonstrates that a didactical situation cannot arise from the same type of model as non-didactical situations (used didactically) of the students. The didactical contract thus exists as a necessary fiction. The play of real situations and of fictional ones is also indispensable.
We will stop here in this evocation of the consequences of the theoretical approach to questions of teaching by the analysis of the teaching of mathematics. Many will perhaps be surprised by the fact that I do produce from it not one single universal or general precept, nor any advice, nor any instructions. The concrete studies in the Theory of Situations indicate in what precise conditions the teaching of a particular notion is possible in a particular form, and that these conditions are never extremal.
The conclusion is nearly always the following: didactical interventions are regulations destined to maintain equilibrium rather than to produce effects directly, and these regulations are specific to the mathematical notion.
The most spectacular consequence of the theoretical studies of the didactical contract has been to show that radical constructivism cannot lead to the acquisition by the student of knowledge aimed at, without didactical interventions.
Other studies have demonstrated, or showed the necessity and functioning of a specific didactical memory, etc.
The epistemology of the teachers
The Theory of Situations takes as a hypothesis that the knowledge developed by an institution is a "legitimate" adaptation, a priori different from that developed by other institutions in other circumstances. The question is thus to know whether the institutions of teaching develop, by professional necessity, original knowledge relative to the acquisition of knowledge, to its role, to its status, etc. Is this knowledge genuinely different from that proposed by various scientific institutions about psychology, sociology, epistemology, etc., which is itself different from that in use in everyday life?
Trivial example: teachers frequently use "carelessness" as a way of qualifying an answer and of characterizing a student.
Carelessness is an inexact response to a question to which the official culture of the class offers a response which is not only easy, but familiar, not worth a new didactic effort. It permits the teacher to elude any didactical action. I don’t know carelessness as an element of medical diagnosis. It is an element of the (spontaneous) psychology of teachers. But it is not a personal relationship to knowledge.
Less trivial example: Should the "intelligent" production of students’ responses follow the outline of a culturally correct proof? Teachers don’t necessarily believe that this is the case, and their practice follows other routes. They may, for instance, act as if they were fine cognativist psychologists, by interpreting the arcane elements of the original thought of a student, by responding and correcting with great rhetorical cleverness. But it’s a question of an exercise of personal knowledge of the teacher which has no place within official knowledge. Concretely, the teacher cannot transform her class into a psychological laboratory. The bad habits of one students do not always have didactical virtues for others — to the contrary! The teacher is thus obligated to practice and profess an "official" model of thought glued onto that which the culture declares intelligible and explicable. The fact of wishing to confuse the organization of knowledge with the laws of its production is manifestly an error, but it is the indispensable consequence of the didactical contract: the teacher cannot rectify all personal trajectories, nor even the collective trajectories if they diverge too far from the final organization of knowledge. It would be too costly, or even technically impossible…whence the conclusion: an epistemology "glued" onto "the current organization of knowledge."
Thus in his practice, his vocabulary, his requirements, etc., the teacher mobilizes "concepts", or "laws" whose object is to permit the action of the student and justify the decisions of the teacher. "How to search?" "What is it to search?", "How to learn?", "How to understand?" etc., are questions which students and teachers of secondary school ask themselves, to which they respond implicitly by their practices, thus bearing witness to a sort of spontaneous and functional, but false, epistemology. This is accompanied by an entire mythology of metaphors and symbols, etc. but the ensemble constitutes a praxeological system which is acceptable from an ergonomic point of view.
Example: in professional mathematics, and in principle, only the validity of the result counts. Relative to rigor, all other considerations: length, complexity, clarifying character, elegance, clarity of style, heuristic nature, etc., are subsidiary. Subtle reasoning or exhaustion by enumeration of cases, inspired intuition or unexpected luck, it suffices to show that the solution indisputably resolves the problem. But a beginning student who acts in that way and for example produces the roots of an equation "by trying 1, -1, I, -I because that often works" has no chance of seeing her solution legitimated (subsequently she will be credited with a certain right to see this type of solution directly.) A solution that one happens on and that miraculously satisfies the given conditions has no value in the epistemology of teachers and very little on tests … because it has no positive didactical function. (This explains why teachers and thus students are reluctant to use the conclusions to look for good values to use in the course of a proof, or to read equalities from right to left, etc.) Thus the conditions for producing a mathematical result are very different, and treated far more vigilantly and intentionally in the didactical situation.
The fact of recognizing that the origin of epistemological belief for teachers is the need to satisfy the needs of their profession is not a value judgment. It could be a truth or an epistemological error and in the two cases be equally useful or even necessary. But it is important not to confuse either the objects or the functions.
The Theory of Situations studies the actual functioning of systems. There exist epistemological "beliefs", of cultural, historical, scientific, etc. origin. They have a function, a justification. They may be true or false, and well- or ill-adapted independently! Things that facilitate the "local" didactical relationship are not always without long-term consequences.
The term "epistemology" covers a larger field than the conception of the genesis and meaning of knowledge, even though it is this part which is the most important for the relationship of the teacher with scholarly society.
The manner in which a particular teacher thinks to produce a didactic genesis which he wants to teach in his classroom should indeed be controlled by a repertoire of explicit or implicit pieces of knowledge of epistemological nature. One could, perhaps, identify it as "the epistemology of that teacher about that notion in that class." But in that case we are talking about a level of specificity which is difficult to observe and deal with. What can be observed is the product, the register of his choices and decisions. Trying to infer from this register a private epistemological repertoire is hazardous except on a few fairly singular points. In addition, things that are particular to one teacher are not very interesting for didactique, where collective and stochastic phenomena dominate.
It would be interesting to establish an inventory of beliefs which form the epistemology of teachers and which are justified by the necessities of their task. But the principal difficulty arises from the fact that all mathematicians practice didactique. And consequently, outside of their domain of research, they share teachers’ didactical conceptions. It is therefore not easy to distinguish an epistemological belief of an expert and that of a teacher. Only a work which is didactical and epistemological and then historical could help do that.
For example, the introduction of the practice of public proofs in the uses of mathematics in Greece in the 5th century BC was a decision initially of didactical nature and origin. Its consequence in the practice of mathematics were gigantic. I strongly suspect — and I realize this is a risky thesis — that the long silence in mathematics in the civilization which "directly" inherited this culture — by which I mean Rome and Byzantium — did not happen by chance, and that the necessity of a proof constituted an enormous epistemological obstacle which weighed heavily on the production and interest of mathematics in those societies. One needs to rethink the opposition between this practice of mathematics which is now classic with the mathematics which is more applied and more willingly esoteric (always practiced in the world.)
The "official" epistemology of mathematicians is very much contaminated by the epistemology of teachers (because the communication and diffusion of mathematics appear as an unavoidable necessity, because mathematicians were good students and frequently good teachers.) Which explains why it can at times be quite false and improper.
The epistemology of teachers is simultaneously
The epistemology of the teachers has as a cognitive function the mixing of these four objects into a single one. For this reason, it is taken by the teachers to be the "real" truth of mathematics, of teaching and of students.
It has been observed that teachers used exactly the same terms to describe their objectives, the knowledge of the students, the explanation of their errors and the means envisaged for repairing them. Consequently, I suspect that teachers have a great deal of difficulty distinguishing the two geneses which constitute the poles of the didactical transposition:
We thus have four organizations of mathematics:
Teachers have a tendency to confuse these two projects with the "official" organization of knowledge in use in teaching and in scholarly society. They therefore take the order determined by an axiomatic exposition of the intended mathematical notion simultaneously as a model of the chronogenesis and the final organization of knowledge.
In this exposition we have restricted ourselves to giving a few examples of the results of the use of the Theory of Situations, but there exist many more.
The place and role of mathematical didactique in education and society
The Theory of Situations in mathematical and scientific didactique
What is didactique of mathematics?
The term is used with different meanings by different countries and institutions. For example, the same course on the teaching of geometry, aimed at the same population of student teachers, might be entitled "Didactique of Mathematics" in a mathematics department or just "Mathematics" in a department or college of education. The matter is complicated by the fact that one often uses the same term to designate an activity, the knowledge and technical means needed for it, and its study, scientific or otherwise.
Thus from the Greek term signifying "to teach" (a piece of knowledge), as opposed to "to educate" (lead students), Comenius derived "didactics" in the sense of the art of teaching, and produced under this title a work destined to combat the dogmatic and scholastic teaching practices in which an institution interposed between the texts and the students in order better to control their religious education. It followed that this term designates everything used in teaching: materials, techniques, terms and pieces of knowledge. As a consequence, the production of these materials: textbooks, software, advice and the art of producing these materials entered into the field of didactics.
Also as a consequence, the study of the teaching of mathematics as a practice or a social project, whatever the discipline or the point of view in which this study is undertaken, entered into the field of mathematical didactics: the psychological study of mathematical behavior of a student in or out of school, the anthropological or ethnological study of the activities of teachers, the linguistic study of scholarly discourse on chance phenomena, etc.
But in the 19th century the meaning of "didactical" spread to anything denoting the intention of teaching — in particular in the ridiculous but fairly common situation where the student has no desire to learn. This pejorative connotation which associated "didactical" and "pedantic" eventually made it impossible to use the word didactic in certain countries.[Translator’s note: this includes the English-speaking countries, which is why we have chosen to retain the French "didactique" in a number of situations.]
Thus today the term didactical refers to the activity itself of teaching mathematics, the art and knowledge necessary for doing it, the art of preparing or producing the means for this activity, the study of this teaching and everything that manifests itself in it, as social project, as socio-historical fact, as phenomenon…
Since the combination of classical disciplines is not equipped to give a simple explanation for the set of didactical phenomena, nor to offer appropriate techniques, specific theories (home-made, some say, not without a certain measure of scorn) have had to be developed (methodology, theories of teaching.) The most interesting of those are the ones which make it possible to take control of — to regulate — the consequences of importing results from other disciplines in teaching.
Applied general didactics or proper science?
For many researchers, such theories should first be general, that is independent of content, to be applied subsequently to a particular content. Mathematical didactics would first be a general theory of didactics. My position on this subject is far more fine-tuned. Didactique begins with the determination of its object: a particular piece of knowledge. There is no reason to think that the invention or practice of geometry can be the same adventure as that of algebra. The hypothesis that the construction of all knowledge followed identical processes seems to me to be contradicted by history and by my practice of mathematics. For the student as for humanity, a new piece of knowledge is a lot more than a simple application of a more general knowledge, and that’s what makes it interesting. Swallowing whole the idea of a preceding general didactique seems to me tantamount to eliminating from the study everything which is proper to didactique. General didactics can only, in my view, be a chancy metadidactics. And that is why the Theory of Situations starts with the study and modeling of didaactical situations proper to this or that specific piece of knowledge.
I cannot say whether the Theory of Situations, or one of its metamorphoses, is equipped to furnish mathematical didactique with the theoretical and experimental framework needed to make it an entire separate science. I can only hope so. It offers itself as a scientific approach to the set of problems posed by the diffusion of mathematics, in which the specificity of the knowledge taught is engaged and plays a significant role.
Scientific Didactique
It will not have escaped the attentive listener, if there are any left after this long an exposition, that putting mathematical knowledge into situations renovates its presentation to students. Having knowledge function brings into evidence its usefulness and its role within a milieu. It puts the role of mathematical theorization back into the perspective of its applications.
On another front, the analysis of transpositions can furnish an experimental context for the problem of adapting mathematics to teaching with a view to different institutions. Should the theme of distributions be taught in that engineering school? Or should one be satisfied with a structure which is less powerful but more easily mastered by the students in the available time? The question does not depend on ideological debates, but on models, measures, calculations and experiments.
Interest presented by didactique of mathematics
Interest for teachers
The teacher always expects that didactique will furnish him with at least the essentials of techniques specific to the notions to be taught, compatible with his general educational and pedagogic conceptions:
For example, he wants to know how to make a real scientific activity possible without sacrificing student time for tasks which have no teaching virtue. Situations like "Enlarging the puzzle" demonstrate that students can "construct" a non-taught piece of knowledge, and up to a point reinvest it to resolve new problems. But this situation is not transferable to any other mathematical notion.
Or again the teacher wants to know how to get students to learn to do paper-and-pencil calculations and notably tables even though the intensive use of calculators has trivialized them.
As with all technical objects, the answers will not always have more than relative qualities and will not prevent failure if the teacher lacks the real competencies to put them to work.
The teacher can also expect of didactique some knowledge relative to different aspects of his work:
In a completely different order of idea, didactique can, in due course, help the teacher to modify her status, her training and her relationship to society:
Since didactique explains the real causes of a difficulty in teaching by a phenomenon or a law, it relieves teachers of part of the illegitimate suspicion of incompetence which weighs on them. On the other hand, it specifies their responsibilities and gives means of regulation of their work which could register as constraints. This is the case notably when didactique makes itself the echo and promoter of prescriptions inferred directly and without analysis of the obtained results from other disciplines, or when it takes up without serious study the objurgations of this or that organization or pressure group. Teaching is the last refuge of all collective or individual fantasies, the last closed field in which all ideologies can confront each other in all good conscience. To manage teaching, society arbitrarily applies to it inadequate models: consumerism, industrial productivity, political or religious utopianism, scientism… In these conditions teachers, overloaded with incompatible obligations, with inapplicable prescriptions, with exotic representations, lose the capacity to control the fundamental parameters of their action, when they don’t take advantage of them to carry certain of the responsbilities which are incumbent on them, and which could disappear from general attention.
Let us examine by way of an example the ideology of "the innovation," which has been inflating for a long time in my country and in certain others. An innovation interests certain teachers because it causes them to look into their practices and helps them to fight against obsolescence. It interests everyone who gravitates around teaching: teacher-educators, editors, various people in responsibility, because it nourishes their discourse and justifies their intervention. It interests everyone who is interested in letting it be known that teaching is being done badly, etc. But in making novelty the essential criterion of the value of the proposed action, one destroys its chance of success and shows that it is not improvement of teaching which is aimed at. In effect, the defining characteristic of an innovation is that it disqualifies an old practice in order to replace it with another, and not in order to correct it. One has the empirical illusion that from amongst these hundred blossoms of innovation the teachers will be able to harvest the ones which will work for them, but one innovation chases out the other, it criticizes the former but doesn’t regulate it. Certain pieces of knowledge can no longer be taught, and disappear, not because it has been decided that they have become useless, but because cascades of innovations have caused the ecosystem which permitted them to exist as an object of teaching to disappear. Fashions pass or return without real progress. The ideology of innovation kills innovation.
Which is not to say that didactical conservatism does not present other equally redoubtable inconveniences.
Interest for the training of teachers
By giving teachers an integrating science and a memory proper to the field, didactique allows the creation of a common culture, as well as the taking into account of the experience acquired and the results of scientific research. The dependence of teaching relative to numerous domains of knowledge leads to a discouraging clogging of training. Didactique reduces the resulting redundancies and makes it easier to organize the central courses on the principal activities being aimed at.
Built on a scientific edifice, the engineering that it proposes will not necessarily be accompanied throughout by a practice that is more elegant than that of the best teachers, but it could ameliorate the overall results or prevent certain catastrophes.
The difficulties in training teachers in didactique result from the fact that the work of didactical transposition of didactique itself remains to be done. The volume and complexity of the parcels of research results dispersed among numerous concurrent disciplinary fields has grown far more rapidly than the training time and than the hierarchy of works of synthesis usable for beginners. To understand and use one of these results in a class it is necessary to bring in prior knowledge on all the other subjects, which only certain in-service teachers have available.
It is necessary to assume and respect the necessary existence of a "beginner’s didactique," guaranteeing a minimal professional behavior, which can cohabit during training with a theoretical training which prepares for a more refined use of more advanced knowledge of didactique. The projection of all the "new" ideas is gratifying for the trainer of teachers but it can happen that she is not capable of predicting what her students are going to make of it. Inversely, utilitarianism in the short term of all the training of teachers leads to worse: the illusion of simplicity and the impossibility of understanding and treating the cause of failures.
Interest for parents and the public
What is possible and what is illusory or fallacious? All reforms are stymied by the insufficiencies and the differences of epistemological conceptions between the social partners. The monitoring of education by the public is legitimate, but it requires a certain minimum knowledge and information, and an entire scientific and social hierarchy looking into the different levels of knowledge and of regulation of didactical acts. This model exists in the domain of medicine: the vocabulary of the biologist, that of the doctor and that of the patient are all different. Each has its necessity and its domain of effectiveness in the regulation of medicine. Neither a blind confidence in the professional body nor generalized suspicion is the best solution. But for that it is necessary that minimal didactical repertoires be maintained, used, ordered and "recognized" as legitimate. From this point of view the universal diffusion of everybody’s opinions on each of these subjects, permitted by modern media, has a tendency to destroy the social functioning of these repertoires. With the best of ideological justifications, it destroys the transpositions and poses major problems in the management of all the traditional fundamental systems.
It is moreover on this medical model that certain parents tend to conceive and organize the regulation of the teaching of their children. Difficulties are perceived as illnesses, for which it is suitable to find cures, if necessary with specific institutions which upon occasion find with the help of doctors the means of having their work pass for health care. More and more children and activities are thus pulled out of the communal social project. Collective teaching is contaminated: there has been shown to be a marked tendency to reduce lessons to "remediation" of students’ individual errors, noted in exercises.
These actions are authorized by an individualist and consumerist conception of teaching which is spreading more and more and which increases the confusion. What one learns in school is not only what one will personally need for survival in the future (nobody can know what that is.) It is first of all the culture which society considers to be the minimum necessary for each of its adult members, and in addition the civil service which children fulfill by dealing with the challenges of learning, which permits society to find the different sorts of specialists which it will need. A student doesn’t learn mathematics just for his own needs, but also to offer society a chance to find, when the moment comes, both the mathematicians and the modest users of mathematics which it will need.
Interest for science itself
Improving the production of scientific knowledge without losing control over its validity is a concern for the community, in particular for mathematicians. In order for the communication and the restructuring of knowledge to develop these two activities must enter the social scientific process of evaluation. Didactique would have the vocation to be the means of that entrance if it were to resolve certain of the theoretical problems with which it is faced.
From the moment one touches on the organization of knowledge, one must have discussion with its producers. It is thus in the very heart of the scientific community that didacticians and teachers must win the legitimacy of reorganizing teachable knowledge. These reorganizations moreover are an integrating part of scientific activity. It is too frequently forgotten that the pruning and reorganizing imposed by communication and teaching are necessary and contribute strongly to their evolution.
This point explains why the didactique of a scientific discipline should be placed under the responsibility of that discipline, even if it could be the object of didacticians of diverse scientific origins.
The great difficulty of this function of didactique is that it attempts to teach to research professionals an art which they already practice unconsciously in their work in a manner that they find satisfactory, basing it on a science which they consequently consider obvious or strange, thus useless.
Interest for society as a whole
It is in science, and at an earlier age in mathematics, that students can learn how to establish and manage scientific truth in a democratic society. The means of realizing this project are not easy to invent, nor to activate, but it is even more difficult to make this project and its consequences enter into the culture. Only the penetration of didactique into the culture will make it possible to improve the political management of the diffusion of knowledge and to make its use and creation more democratic.
Mathematics, didactique of mathematics, education and the science of education
Terms and ideology: instruction, teaching, education
The term "mathematical education" has replaced "instruction in mathematics" and even "the teaching of mathematics" in the course of the Sixties. It’s a matter of a progressive enlargement of the assumed ambition. "Instruction" consists of structuring and informing: structuring the student by her knowledge, knowledge by know-how; the emphasis is on the culture to be transmitted. Teaching consists of making someone understand, of making someone know, of making someone learn; the emphasis is on the means of transmitting. Education consists of leading, of raising or lifting; the emphasis is on the whole of the process by which a child becomes an adult.
In these conditions it becomes more difficult today to pretend to treat instruction and teaching without placing them directly in the global framework of education. The respective ambitions of teaching, of methodology, of didactique, of mathematical education and of the Theory of Situations have been evoked sufficiently above. They are legitimate, distinct and complementary. And after all, in sciences, multiple approaches to the same object are not a novelty.
But it appears difficult to deduce from that a social organization suitable for assuring the responsibility for teaching, for training teachers of mathematics and for research in this domain.
In fact, cooperation in imperative and the institutions seem not to be interested in cooperating.
Membership in the sphere of mathematicians
Teachers of mathematics should feel that they belong to the sphere of mathematicians,
[Synopsis of following paragraphs: in fact, the term is generally reserved for the university, for producers of mathematical knowledge in the strict sense. Teachers are thus isolated.]
Membership in the educational sphere
Teachers should feel that they belong intellectually to the educational sphere. But more often this membership is made more by the intermediary of the profession than that of the culture, which is too vast and too disparate. They visit it at best as enlightened amateurs. The two questions which are posed to them are the following:
If the answer to these two questions were negative, it would suffice to juxtapose the two cultures, under a responsibility which might or might not be common and might or might not be a third party, as is done for other professional training at the university level. But the response is not negative, especially for the second, which is easy to demonstrate: having students use theorems or recite them, having students repeat proofs or find them, initiating students into discussions about proof or revealing the exemplary genius of Euclid have very different educational properties.
For another thing, effective teaching cannot happen without the disciplinary and cultural communities being, or feeling themselves to be, called upon on the subject in the view of the public at one moment or another. At these moments the absence of a didactical culture of either one makes itself felt, and likewise the absence of a community capable of assuming the scientific responsibility of this culture and the research that feeds it.
[Synopsis of the following paragraphs: refusal to acknowledge didacticians as belonging to the educational sphere would cause radical estrangement after a generation or two. Brousseau recommends the solution of having didacticians in the scientific departments to which their study belongs, but points out that much of their research is done under the wing of departments of education. The education of new teachers should be a joint responsibility of didacticians and members of the education faculty.]
Conclusions
More than three thousand years after the invention of commerce, economics — science of the conditions for diffusing material goods necessary for people — took two hundred and fifty years to begin to emerge from fantasies. It is far from offering satisfactory solutions.
To educate the two billion or so non-adults there ought to be about 50 million people in the world occupying themselves professionally with their teaching and their education by the side of some four billion parents.
The number of creators and initial diffusers of science and techniques is probably considerably lower than one million persons. If the target of didactique is very large, the source is no less so.
Now the scientific study of phenomena of the diffusion of scientific knowledge itself mobilizes only a handful of researchers, dispersed in different and sometimes concurrent institutions, scattered about on divergent research routes. The paucity of means of elaboration and of diffusion of didactical knowledge is shown.
Meanwhile, despite certain current winds, sometimes in a contrary direction, mathematical didactique is off to a not-so-bad start and making progress. I am convinced that it will enter more and more into the scientific and social practices and that it will contribute to the improvement of education for all children.
Any questions or comments on this article would be much appreciated. Please send them to warfield@math.washington.edu