This website contains supplementary material for the paper Quartics and Their Bitangents, authored by Daniel Plaumann, Bernd Sturmfels, and myself. Below there is code in SAGE for computing the topological type of a real quartic and creating examples where all of the bitangents, matrix representations and Gram matrices are rational. Please feel free to email me with comments or questions.
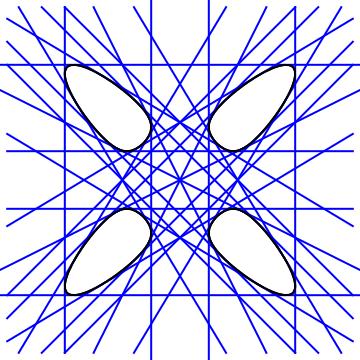
In 1873, Zeuthen showed that there are six different topological types of real smooth quartics and Klein later showed that each of these types forms a connected component in the space of smooth quartics. The type of a quartic determines its number of real bitangents, real Gram matrices of rank 3, and real linear matrix representations. Given a real linear matrix representation of the quartic, one can determine many of these numbers by looking at the number of real points of the corresponding Cayley octad.

One can also construct a quartic from a Cayley octad. If the Cayley octad consists of eight rational points, then all 28 bitangents, 36 linear matrix representations and 63 rank-3 Gram matrices of the quartic are rational. From the table, we see that the real variety of each such quartic consists of four ovals. SAGE code that computes all of these objects starting from seven of the eight points of a Cayley octad can be downloaded here.
In his 1855 paper, "Über die Doppeltangenten der Curven vierter Ordnung", Hesse uses a linear matrix representation and Cayley octad to label the 28 bitangents with pairs of numbers 1, . . . , 8. He then explicitly computes the permutation of these labels induced by the 35 other linear matrix representations. These permutations are listed in the following 36 by 28 table (which appears on page 318 of Hesse's paper).
