... --> Z/pn --> Z/pn-1 --> ... --> Z/p2 --> Z/pwhere each map is reduction mod p; that is, it's the map that sends 1 to 1. (Since these are ring maps, the inverse limit has a ring structure, which might play a role in your answer.)
Also, with p still a prime, describe the direct limit (a.k.a. the "colimit") of the sequence
Z/p --> Z/p2 --> ... --> Z/pn-1 --> Z/pn --> ...where each map sends the generator 1 to the element p. (These are group maps but not ring maps, so the direct limit need not have a ring structure.)
When I say "describe", I mean that, ideally, you should relate these to familiar groups and/or rings (for some value of the word "familiar").
References on direct and inverse limits: McCleary's book, page 67. Any good book on homological algebra should work, too; you could try Weibel's book An introduction to homological algebra, or Mac Lane, Categories for the working mathematician. Also Hatcher, Algebraic topology, page 243 (direct limits) and page 312 (inverse).
- Answer: the inverse limit is isomorphic to the p-adics. The direct limit is isomorphic to Q/Z(p), and also to Z[1/p]/Z.
- Answer: for each non-negative i, Tori(k,k) = k = Exti(k,k).
- compute H*(
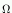 Sn;Z)
as an algebra, for n>1 (partial answer: copy of
Z in each dimension divisible by
n-1).
Sn;Z)
as an algebra, for n>1 (partial answer: copy of
Z in each dimension divisible by
n-1).
- Answer: when n is odd,
it's a "divided power algebra" on a class in dimension
n-1 [standard notation:
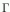 (x)].
That is, one can choose a generator
xj for the piece in
dimension j(n-1) for each
j, so that the product structure is given by
(x)].
That is, one can choose a generator
xj for the piece in
dimension j(n-1) for each
j, so that the product structure is given by
xi xj = (i+j choose i) xi+j. When n is even, it's a tensor product of an exterior algebra on a class in dimension n-1 with a divided power algebra on a class in dimension 2n-2.
- Answer: when n is odd,
it's a "divided power algebra" on a class in dimension
n-1 [standard notation:
- Compute H*(
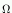 CP
CP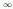 ;Z)
as an algebra, using the fact that H*(CP
;Z)
as an algebra, using the fact that H*(CP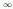 ;Z)
= Z[x], with x in
dimension 2.
;Z)
= Z[x], with x in
dimension 2.
- Answer: Hi = Z if i is 0 or 1; otherwise it's 0. The algebra structure is the only possible one: it's an exterior algebra on a class in dimension 1.
- Compute as much as you can of
H*(
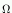 2S3;Z),
as an algebra. If you don't make much progress, compute
the cohomology of
2S3;Z),
as an algebra. If you don't make much progress, compute
the cohomology of 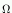 S3
and of
S3
and of 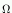 2S3
with coefficients in Q (should
be easy) and with coefficients in
Fp for each prime
p (more interesting). Note that you can compute
H*(
2S3
with coefficients in Q (should
be easy) and with coefficients in
Fp for each prime
p (more interesting). Note that you can compute
H*(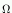 S3;R)
for any commutative ring R by taking the answer
for part 1 and tensoring with R, since the groups
in part 1 are all free.
S3;R)
for any commutative ring R by taking the answer
for part 1 and tensoring with R, since the groups
in part 1 are all free.
- Partial answer: it's complicated.
Here are the first few groups:
Starting in dimension 9, you start getting Z/5 summands. Indeed, for each prime p there is a Z/p summand in dimension 2p-1.i Hi( 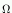 2S3;Z)
2S3;Z) 0 Z 1 Z 2 0 3 Z/2 4 Z/2 5 Z/2 + Z/3 6 Z/2 + Z/3 7 Z/2 + Z/2 + Z/3 From a different point of view: if you do everything with rational coefficients, then the cohomology of the base space
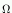 S3 is
isomorphic to a polynomial algebra on a class in
dimension 2, so the spectral sequence looks just
like the previous part. So with rational
coefficients, the cohomology of
S3 is
isomorphic to a polynomial algebra on a class in
dimension 2, so the spectral sequence looks just
like the previous part. So with rational
coefficients, the cohomology of
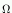 2S3
is an exterior algebra on a class in dimension 1.
2S3
is an exterior algebra on a class in dimension 1.
With mod p coefficients, the cohomology of the base space is isomorphic to the algebra Fp[x2,x2p,x2p2, ...]/(xip). One can use this description to determine the mod p cohomology of
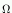 2S3
in as large a range of dimensions as you have
patience for.
2S3
in as large a range of dimensions as you have
patience for.
- Partial answer: it's complicated.
Here are the first few groups: