Math 124, Sections E and G: notes on the chain rule
I want to point out several common applications of the chain
rule. The first is in Section 3.5 of the book, the boxed formula
labeled "The Power Rule Combined with the Chain Rule": if
u=g(x) is a function of x, then you can compute
the derivative of the nth power of u. The
result is (with three different notations)
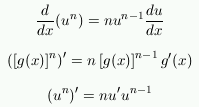
The chain rule also gets combined with the exponential
function frequently:
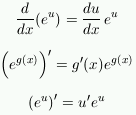
For example, in class on Monday, we needed to compute the
derivative of the function e-x3
+ 2x2 - x+ 6. In words, the
answer is this exponential function multiplied by the derivative
of the exponent. In symbols, this is (-3x2 +
4x - 1) e-x3 +
2x2 - x+ 6.
The quotient rule: If you have problems
remembering the quotient rule, or if you want to know how to
derive it, use the chain rule and the product rule: since
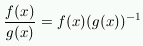 , then when you
take the derivative, you get:
, then when you
take the derivative, you get:
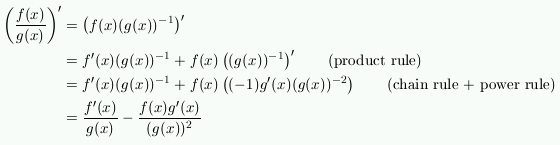
Now if you put everything over a common denominator, you get the
quotient rule.
For example, if you want to compute the derivative of
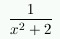 , you can either
use the quotient rule (with f(x) = 1, g(x) =
x2 + 2) or rewrite the original function
as
, you can either
use the quotient rule (with f(x) = 1, g(x) =
x2 + 2) or rewrite the original function
as 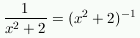 , and then
use the power rule combined with the chain rule. Using this
second method, the answer is
, and then
use the power rule combined with the chain rule. Using this
second method, the answer is
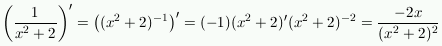 .
.
Of course, you'll get the same answer using the quotient rule; the
point is, you can choose which method to use. Some people (some
mathematicians, even) never memorize the quotient rule; they just
use the combination of the product rule, chain rule, and power
rule instead.
Questions or comments? E-mail me at palmieri@math.washington.edu.
Back to Math 124 home page.
Go to John Palmieri's home page.
Last modified: Mon Apr 29 12:14:20 PDT 2002
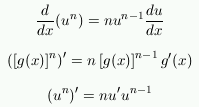
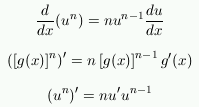
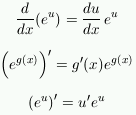
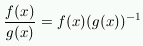 , then when you
take the derivative, you get:
, then when you
take the derivative, you get:
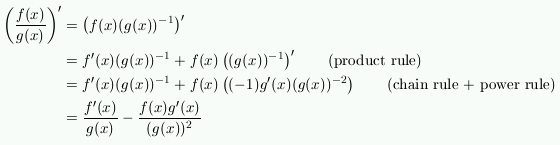
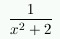 , you can either
use the quotient rule (with f(x) = 1, g(x) =
x2 + 2) or rewrite the original function
as
, you can either
use the quotient rule (with f(x) = 1, g(x) =
x2 + 2) or rewrite the original function
as 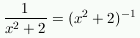 , and then
use the power rule combined with the chain rule. Using this
second method, the answer is
, and then
use the power rule combined with the chain rule. Using this
second method, the answer is
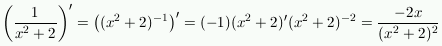 .
.