Mathematics 403 Final Exam Solutions

1. Let A be a real $n \times n$ matrix. Prove that the following are equivalent:

(i)

A is orthogonal (meaning that A^t = A^-1, or equivalently, A^tA = I).

(ii)

The columns of A are mutually orthogonal unit vectors (with respect to the standard dot product).

(iii)

A preserves the dot product (meaning that $(X \cdot Y) = (AX \cdot AY)$ for all $X,Y \in \mathbf{R}^{n}$).

SOLUTION. I'll start by showing (i) $\Longleftrightarrow$(ii). Let v₁, v₂, ..., v_n denote the columns of A. The (i,j)-entry of A^tA is the dot product of the ith row of A^t with the jth column of A. Of course, the ith row of A^t is the same as the ith column of A, so the (i,j)-entry of A^t A is $(v_{i} \cdot v_{j})$. Thus A^t A = I if and only if

$$(v_{i} \cdot v_{j}) = \begin{cases} 1 & \text{if $i=j$ ,} \\ 0 & \text{if $i \neq j$ }. \end{cases}$$

In other words, A^t A = I if and only if the vectors v₁, ..., v_n are mutually orthogonal unit vectors.

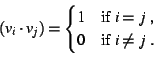
Now I'll show (i) $\Longrightarrow$ (iii).

$$(AX \cdot AY) = (AX)^{t} AY = X^{t} A^{t} A Y,$$

so if A^tA = I, this equals $X^{t}Y = (X \cdot Y)$, as desired.

Finally, I'll show (iii) $\Longrightarrow$ (ii). Given (iii), I know that $(e_{i} \cdot e_{j}) = (Ae_{i} \cdot Ae_{j})$, but Ae_i and Ae_j are the ith and jth columns of A, respectively. Since the vectors e₁, ..., e_n are orthonormal, then so are the vectors Ae₁ = v₁, ..., Ae_n = v_n.

2. Draw a wallpaper pattern with a cyclic group for its point group; draw a wallpaper pattern with a dihedral group for its point group.

SOLUTION. See page 173 for lots of examples. The cyclic group pictures don't have any reflections; the dihedral group pictures will have reflections.

3(a). Let G be a group, S a G-set, x an element of S. Recall that the orbit of x, O_x, is this subset of S:

$$O_{x} = \{ y \in S \,:\,y = gx \ \text{for some $g \in G$ } \}.$$

The stabilizer of x, G_x, is this subgroup of G:

$$G_{x} = \{ h \in G \,:\,hx = x \}.$$

Define a map $\phi : G/G_{x} \longrightarrow O_{x}$ by $\phi (aG_{x}) = ax$. Prove that $\phi$ is a well-defined bijection.

SOLUTION. To show that $\phi$ is well-defined, I have to show that if aG_x = bG_x, then $\phi (aG_{x}) = \phi (bG_{x})$; i.e., I have to show that ax = bx. Well, aG_x = bG_x if and only if $b^{-1}a \in G_{x}$, in which case (b^-1a) x = x. ``Multiply'' both sides by b: ax = bx, as desired.

Running this argument backwards shows that if $\phi (aG_{x}) = \phi (bG_{x})$, then aG_x = bG_x: $\phi$ is one-to-one.

Finally, I have to show that $\phi$ is onto. Given $y \in O_{x}$, then y=gx for some $g \in G$; thus $y = \phi (gG_{x})$.

3(b). Let p be a prime number. Recall that a p-group is a group which has order pⁿ for some n. Prove that the center of a p-group has order larger than 1.

SOLUTION. Let G be a p-group, and consider the class equation for G:

$$p^{n} = 1 + \text{(other terms)}.$$

Each of the other terms must divide the order of G, and so must be pⁱ for some $i \leq n$. p divides the left-hand side and p divides each term pⁱ where $i \geq 1$, but p doesn't divide 1, so there must be more than one 1 on the right side of the equation: the class equation must look like

$$p^{n} = \underbrace{1 + 1 + \dotsb + 1}_{j} + \text{(other terms)},$$

where here the other terms are of the form pⁱ with $1 \leq i \leq n$. The number j must be larger than 1. (In fact, it must be a multiple of p, but I don't really care about that right now.) Now, remember that the terms in the class equation are the sizes of conjugacy classes. If the conjugacy class of an element x has exactly one element in it, that element must be x (since every element is always conjugate to itself: x = 1 x 1^-1). Thus gxg^-1 = x for every $g \in G$; equivalently, gx = xg; equivalently, x is in the center of G. Thus the center of G has j elements, where $j \geq 2$.

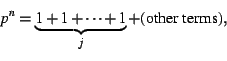
4. Let V be a finite-dimensional real vector space and let $\langle \;, \, \rangle$ be a symmetric positive definite bilinear form on V. For any subspace W of V, let $W^{\perp}$ be the orthogonal complement of W:

$$W^{\perp} = \{ u \,:\,\langle u, w \rangle=0 \ \text{for all} \ w \in W \}.$$

Show that $V = W \oplus W^{\perp}$; in other words, show:

(a) $W \cap W^{\perp} = 0$.

SOLUTION. Assume that $w \in W \cap W^{\perp}$. Since $w \in W^{\perp}$, then w is orthogonal to everything in W; in particular, $\langle w, w \rangle = 0$. Since the form is positive definite, though, $\langle w, w \rangle$ is positive for any nonzero vector w; thus w must be zero. So the only vector in both W and $W^{\perp}$ is the zero vector.

(b) Every vector $v \in V$ can be written in the form v = w + u where $w \in W$ and $u \in W^{\perp}$. [Hint: choose an orthonormal basis for W.]

SOLUTION. Let w₁, ..., w_r be an orthonormal basis for W. (I mean orthonormal with respect to the form $\langle \;, \, \rangle$. I know that there is an orthonormal basis since the form is positive definite--use the Gram-Schmidt procedure, for instance.) I want to write

$$v = c_{1} w_{1} + \dotsb + c_{r} w_{r} + u,$$

where $u \in W^{\perp}$. In other words, I want to choose the scalars c_i so that

$$v - c_{1} w_{1} - \dotsb - c_{r} w_{r} \in W^{\perp}.$$

If I want to check that a vector is in $W^{\perp}$, it suffices to check that it's orthogonal to each w_i, so I compute this:

$$\langle w_{i}, v - c_{1} w_{1} - \dotsb - c_{r} w_{r} \rangle... ...angle w_{i}, w_{i} \rangle = \langle w_{i}, v \rangle - c_{i}.$$

(I'm using the fact that the w_i's are orthonormal.) So if I want this to be zero, I set $c_{i} = \langle w_{i}, v \rangle$.

In other words, for any $v \in V$,

$$u = v - \sum_{i=1}^{r} \langle w_{i}, v \rangle w_{i} \in W^{\perp},$$

so v can be written as the sum of something in W (the sum above) with something in $W^{\perp}$ (the vector u).

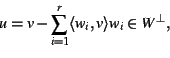
5. Let A be a real symmetric $n \times n$ matrix. We know that there is an invertible matrix Q so that QAQ^t is diagonal, such that each diagonal entry is either 1, -1, or 0. Recall that in this situation, the signature of A is the pair of numbers (p,m), where p is the number of 1's on the diagonal of QAQ^t, and mis the number of -1's. Show that p is equal to the number of positive eigenvalues of A and m is equal to the number of negative eigenvalues. [Hint: use the spectral theorem.]

SOLUTION. By the spectral theorem, there is an orthogonal matrix P so that PAP^t = PAP^-1 is diagonal, with the eigenvalues as the diagonal entries. Let $\lambda_{1}$, ..., $\lambda_{n}$ be the eigenvalues. Define a matrix C as follows: C is diagonal, and the (i,i)-entry is

$$\begin{array}{cc} 1/\sqrt{\vert\lambda_{i}\vert} & \text{if $... ...i} \neq 0$ ,} \\ 1 & \text{if $\lambda_{i} = 0$ .} \end{array}$$

Then C is invertible and C^t = C. Now look at (CP) A (CP)^t = C(PAP^t)C^t: since PAP^t is diagonal with ith diagonal entry $\lambda_{i}$, then C(PAP^t)C^t is diagonal with ith diagonal entry

$$\begin{array}{cc} 1 & \text{if $\lambda_{i} > 0$ ,} \\ -1 & ... ...da_{i}< 0$ ,} \\ 0 & \text{if $\lambda_{i} = 0$ .} \end{array}$$

CP is invertible, so let Q=CP: then QAQ^t is of the right form, and it has signature (p,m), where p is the number of positive eigenvalues of A and m is the number of negative eigenvalues.

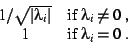
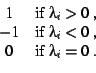
6. Let U(n) be the set of complex $n \times n$ unitary matrices. Show that the product of two unitary matrices is unitary, and the inverse of a unitary matrix is unitary; in other words, show that U(n) is a subgroup of GL_n(C).

SOLUTION. Recall that a matrix A is unitary if and only if AA^* = I. If A and B are unitary, then (AB)(AB)^* = ABB^*A^* = A(BB^*)A^* = A(I)A^* = I, so AB is unitary. If A is unitary, then A is invertible with A^-1 = A^*; I need to check that A^* is unitary: A^*(A^*)^* = A^*A. We know from last quarter that if C and D are square matrices with CD = I, then DC=I; thus A^*A=I, as desired.

7. Let A be a real symmetric matrix, and define a bilinear form $\langle \;, \, \rangle$ on Rⁿ by $\langle X, Y \rangle = X^{t}AY$. Of course, there is also the ordinary dot product $(X \cdot Y) = X^{t} Y$.

True or false: If A is a real symmetric matrix, then the eigenvectors for A are orthogonal with respect to both the ordinary dot product $(\, \cdot \,)$ and the bilinear form $\langle \;, \, \rangle$. Give a proof or a counterexample.

SOLUTION. This is true. The spectral theorem says that the eigenvectors are orthogonal with respect to the ordinary dot product. Now assume that X and Y are eigenvectors, with $AY = \lambda Y$. Then

$$\langle X, Y \rangle = X^{t} A Y = X^{t} (\lambda Y) = \lambda (X^{t}Y) = \lambda (X \cdot Y).$$

Since X and Y are orthogonal with respect to the ordinary dot product, this is zero; hence they're orthogonal with respect to the form defined by A, too.

8. Describe the Gram-Schmidt procedure.

SOLUTION. This is a procedure for constructing orthonormal bases, given a symmetric positive definite bilinear form on a finite-dimensional real vector space V. More precisely, you start with any basis for V, and the Gram-Schmidt procedure tells you how to alter it, inductively, to get an orthonormal basis.

Even more precisely, suppose V is a vector space with bilinear form $\langle \;, \, \rangle$, satisfying the conditions above. Let $(v_{1}, \dotsc, v_{n})$ be a basis for V. To construct an orthonormal basis $(w_{1}, \dotsc, w_{n})$, first normalize v₁: let

$$w_{1} = \frac{1}{\sqrt{\langle v_{1}, v_{1} \rangle}} v_{1}.$$

Then w₁ is a unit vector.

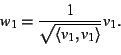
Suppose now that we've constructed mutually orthogonal unit vectors w₁, ..., w_k-1 out of the v_i's. Define a vector was follows:

$$w = v_{k} - \sum_{i=1}^{k-1} \langle v_{k}, w_{i} \rangle w_{i}.$$

Then w is orthogonal to each w_i, so normalize it to get w_k:

$$w_{k} = \frac{1}{\sqrt{\langle w, w \rangle}} w.$$

Go to the Math 403 home page.

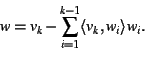
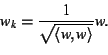
Go to John Palmieri's home page.