Abstract:

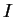
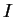
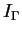
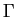
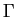
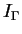
We define a set of invariants of a homogeneous ideal $ I$ in a polynomial ring called the symmetric iterated Betti numbers of $ I$. 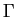We prove that for $ I_{\Gamma}$, the Stanley-Reisner ideal of a simplicial complex $ \Gamma$, these numbers are the symmetric counterparts of the exterior iterated Betti numbers of $ \Gamma$ introduced by Duval and Rose, and that the extremal Betti numbers of $ I_\Gamma$ are precisely the extremal (symmetric or exterior) iterated Betti numbers of $ \Gamma$. 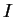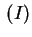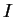We show that the symmetric iterated Betti numbers of an ideal $ I$ coincide with those of a particular reverse lexicographic generic initial ideal Gin$ \,(I)$ of $ I$, and interpret these invariants in terms of the associated primes and standard pairs of Gin$ \,(I)$. 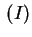We close with results and conjectures about the relationship between symmetric and exterior iterated Betti numbers of a simplicial complex.