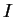
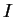
We describe a new family of free resolutions for a monomial ideal , generalizing Lyubeznik's construction. These resolutions are cellular resolutions supported on the rooted complexes of the lcm-lattice of . Our resolutions are minimal for the matroid ideal of a finite projective space.