Abstract:

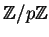
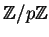
Necessary conditions on the face numbers of Cohen-Macaulay simplicial complexes admitting a proper action of the cyclic group $ \mathbb{Z}/p\mathbb{Z}$ of a prime order are given. This result is extended further to necessary conditions on the face numbers and the Betti numbers of Buchsbaum simplicial complexes with a proper $ \mathbb{Z}/p\mathbb{Z}$-action. 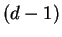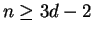Adin's upper bounds on the face numbers of Cohen-Macaulay complexes with symmetry are shown to hold for all $ (d-1)$-dimensional Buchsbaum complexes with symmetry on $ n\geq 3d-2$ vertices. 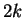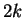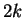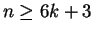A generalization of Kühnel's conjecture on the Euler characteristic of $ 2k$-dimensional manifolds and Sparla's analog of this conjecture for centrally-symmetric $ 2k$-manifolds are verified for all $ 2k$-manifolds on $ n\geq 6k+3$ vertices. Connections to the Upper Bound Theorem are discussed and its new version for centrally symmetric manifolds is established.