Quick Overview of S_n (the symmetric group on n elements)

Definition:

S_n is the group of all possible bijections of X à X where X is any set with n elements (i.e. permutations of the elements of X).

In general, we take X={1,2,…,n} and we use one of two notations for the elements of S_n:

1) PERMUTATION NOTATION (for S₅):

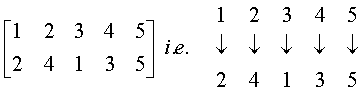
2) CYCLE NOTATION (for S_n, n>4):

MULTIPLICATION: Right-to-Left:

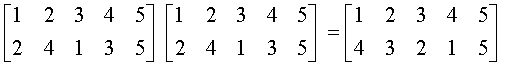
-- Every cycle can be written as a product of disjoint cycles

-- Disjoint cycles commute

-- A cycle is EVEN if it has odd length (because it can be written as an even number of transpositions = 2-cycles).

Example: (1 2 3)=(1 3) (1 2) is even,

while (1 2 3 4)=(1 4)(1 3)(1 2) is odd.

Definition: The ALTERNATING GROUP A_n is the subgroup consisting of even permutations.

(prove it’s a subgroup!)

IDENTITY:

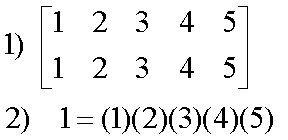
1-cycles get suppressed

INVERSES: just reverse all arrows

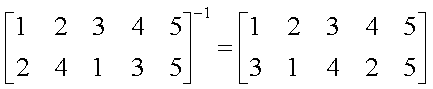
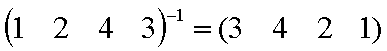
REMARKS:

1) |S_n| = ? =n!

2) |A_n|= ?=n!/2

Cayley’s Theorem: Every finite group G is isomorphic to a subgroup of a symmetric group.

Fun uses: Rubik’s Cube, the 15-puzzle, etc.

See, e.g., http://members.tripod.com/~dogschool/rubikscube.html