In class today we had a problem where we had to compute 1+1+2+3+...+99+100 = 5051. Like many math problems, there are three general ways to attack such a problem: spend lots of time, recruit lots of people to help, or come up with a more clever way. I would recommend the third. In the two questions below, you might find it useful to use pairs or the fact that 1+2+3+...+100 = 5050 (as derived in class) and 1+2+3+...+200 = 20,100.

a. What is the sum of the first 100 even numbers (i.e. 2 through 200).

b. What is the sum of the first 100 odd numbers (i.e. 1 through 199).

I class we talked about chopping a circle into smaller pieces. These next questions ask about chopping a square into smaller squares. This is much more restrictive. For example, starting with



I can divide it up into, say 4 squares:



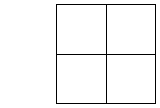
25 squares:



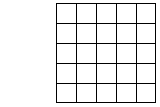
10 squares:

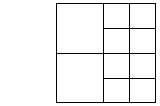or

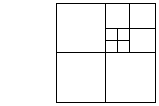
but it is impossible to divide it up into, say, extactly 3 squares.

a. How could you divide the square into exactly 13 smaller squares? 9 squares?

b. For any large enough number n, it is always possible to divide the larger square into exactly n smaller squares. What is the largest number such that it is impossible to divide the square into that many smaller squares? Please explain, i.e. justify why it cannot be done for your answer but can be done for any greater number.