This homework deals with finding Eulerian paths in graphs (paths that go along each edge exactly once), though it might not look so on first glance. Either rephrase these problems as finding paths on graphs or apply the same reasoning directly to the problem.

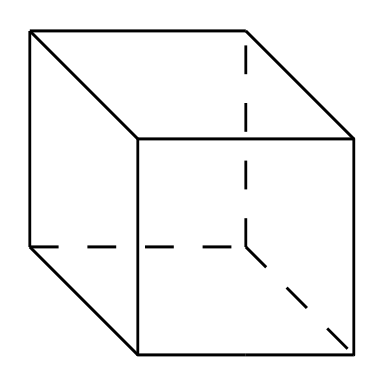
1. Suppose I unfold a paperclip and find that it is 12 cm. long. I want to fold it into a wire-frame cube that is 1cm by 1cm buy 1cm. Can this be done without cutting the paperclip into smaller pieces? If not, how many cuts do I have to make to be able to form my cube?

2. I went on a journy in my time machine and came back with Euler's shoelace.

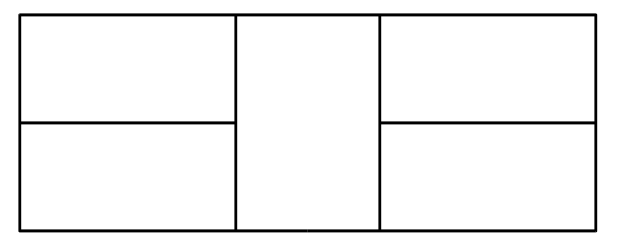
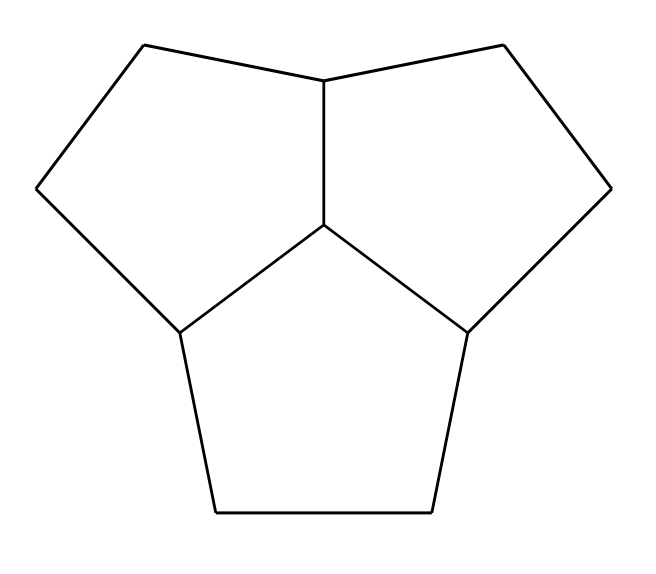
He has been trying to place it on this grid so that it crosses each of the 16 line segments exactly once. Can this be done? If so, deminstrate. Otherwise, justify why not.

What about the two other grids below? (Hint: try these first.)