| Home | 1st Year Circle | 2nd Year Circle | Archive | About | Math Hour | Math Hour Olympiad |
Here you can see the weekly newsletters containing updates of what we're up to each week. This newsletter is emailed out shortly after a Math Circle meeting. If you're not receiving these email updates but want to be, just let Alex know via email at alex.vaschillo@gmail.com
Today we continued to study geometry and proved (using several different approaches) that the area of a circle is pi*r^2. In the process of deriving the area of a circle we touched on some calculus and calculated the areas under the curves x^2 and x^3. We proved that the volume of a cone with a base of area B and height h is always Bh/3, regardless of the shape of the base, and then discussed how we could extend our approach to calculating the area of a circle to calculate the volume of a sphere (or an n-sphere).
In the last half hour of class we began a generalization of geometry that will be the source of discussion for the next few weeks: topology. We defined open and closed sets on the number line and looked at many examples of each.
Today we had a fun lecture on n-dimensional geometry. We discussed how to represent shapes in 4 dimensions, calculated the number of vertices and edges of an n-dimensional cube, and discussed how we could determine the volume of an n-dimensional sphere. We came across the Gamma function, an extension of the factorial function to non-integers and proved that an infinite-dimensional orange is nothing but peel. (We showed this by calculating the volume of an n-sphere with radius 1 and the volume of another sphere with with radius r < 1. This constrcution is reminicent of an orange, where the volume between the two spheres is the peel. The ratio of the volume of the smaller sphere to the large sphere goes to 0 as n goes to infinity, meaning that the peel becomes a larger and larger part of the orange.)
Today we finished our discussion of game theory by deriving a winnin strategy for Nim. The stragey is to write the number of stones in each pile in binary and write these numbers on top of each other. Then, make moves to ensure that the number of zeros in each column is even. For a more detailed explanation, see here.
We then discussed the relationship between Nim and Domineering and looked at several different variants of both (most notably the misere versions).
Today we continued our discussion of Domineering and Hackenbush and assigned points to different board positions - positive points denoted a winning position for the player about to move on such a board, and negative points denoted a losing position for a player who is about to move on this board. Hackenbush is a very well studied game and there are many sources of information online (e.g. here).
Today we also began discussing the game Nim. We will discuss the strategy behind Nim next week.
No class!
Today we talked about prime distance graphs. A graph is a prime distance graph if its vertices can be numbered with distinct integers such that the difference between the numbers on any pair of connected vertices is prime. We looked at several examples of graphs that were and were not prime distance graphs.
We also called a graph graceful if you could number its vertices with distinct integers such that the differences between pairs of connected vertices forms the set $\{1,2,3,\ldots\}$. We found that all paths are graceful, but cycles of length 1 or 2 (mod 4) are not graceful. Finally, we discussed several open problems such as whether all trees are graceful.
Today we had a fun lesson about different ways to sort numbers.
Over the course of a few hours we discovered several algorithms.
We came up with our own names for them, but these algorithms are actually very well known by the following names:
For each of these we discussed how many operations we would have to preform to completely sort a list of $1000$ numbers (looking only at worst case scenarios)- we found that merge sort outpreforms the others by far. In fact, we found that if we are sorting $n$ numbers then merge sort uses only $n\log n$ operations while all the others use $n^2$. For fun, I encourage you to visit this site to see examples of these (and other) sorting algorithms in action.
Finally, we ended class by briefly discussing the difference between polynomial-time alogirhtms and non polynomial time alogithms. This difference is the foundation of the P vs. NP problem.
Today we dedicated all two hours of class to group theory. We looked at several examples of groups that contained smaller groups within them - we called these smaller groups subgroups By looking at several examples we noticed a pattern: the number of elements of a subgroup always divides the number of elements of the bigger group. This fact is known as Lagrange's Theorem, and we spent the remainder of class proving this. We began by considered what happens when every element of a subgroup is multiplied (from the left) by some element of the bigger group. The result is not a group, but had enough interesting properties to warrant a name - we called this a coset of the subgroup. We then discovered, and later proved, that the set of cosets of a subgroup partition the group: none of the cosets overlap and together they completely cover the bigger group. This allowed us to conclude Lagrange's Theorem.
No class on account of BAMO
This was our last meeting before the BAMO. We worked through problem 1 from BAMO 2009 and problem D from BAMO 2013 Good luck on the BAMO!
We spent the second half of class defining the concept of a mathematical group (the definition we used in class is in the homework). We showed that the set of operations that permute the corners of the triangular and the rectangular mattresses from last week are both groups (specifically, these are $D_3$ and the Klein group, respectivly). We proved some properties of groups such as:
Today we spent the first part of class discussing problem 1 from BAMO 2008.
We spent the remainder of class on our new topic: group theory. We started by looking at two examples. The first is the mattress problem, where we look at the four different operations (one rotation, two reflections, and doing nothing) that can be performed on a rectangular mattress that permute its corners and showed, by writing out a multiplication table for these operations, that it is impossible to repeatedly apply a single operation to cycle through all four possible orientations of the mattress. We then looked at the same problem but with an equilateral triangular, 2 dimensional mattress. For such a mattress there are six legal origentations of the mattress and six operations that permute the corners (3 reflections, 2 rotations, and doing nothing). By looking at the multiplication table of these operations we found that again, there is no way to choose a single operation that allows you to cycle through all six possible orientations of the mattress.
We will see next week that these groups of operations form what is known as a group.
We spent the first half of class working through problems A and C from BAMO 2012. Again, we are emphasising the ability to write solutions and spent a while discussing how we would structure our arguments on paper.
We spent the second half of class finishing our conversation about voting by discussing Arrow's impossibility theorem, which states that the only voting method that is simultaneously not backwards and satisfies IIA is the monarchy. It is surprising that there is only one voting system that satisfies such reasonable and desirable requirements is a system of voting that seems so unfair.
Today we spent the first half of class working through problems C BAMO 2013 and problem D from BAMO 2010. We discussed how we would concisely write out our solutions. In the second half of class we listed which of our voting systems satisfies which of the criteria that we established last week (we basically filled in the table from last week's homework). We found that the voting systems were very different regarding which criteria they satisfy and, to our surprise, the monarchy satisfies the largest number of criteria.
Note: On the evening of February 25 (exact time to be decided), the UW Math Circle will be administering the Bay Area Math Olympiad (BAMO). This is a mathematics competition that is very much in the style of our Math Circle and is quite similar to the UW Math Hour Olympiad - the competition consists of 4-5 problems that students are given 4 hours to solve and write up. We strongly encourage everyone to participate in the BAMO and will be spending a significant amount of our meeting time in the next few weeks preparing for the competition. For more information about the BAMO, visit their website and especially look at some of the previous problems. Please do not register yourself for the exam. We will handle registration for UW Math Circle students - if you are interested in competing let me know and I will make sure that you are registered.
With that, here is a summary of what we discussed last Thursday. We began by talking about the following problem:
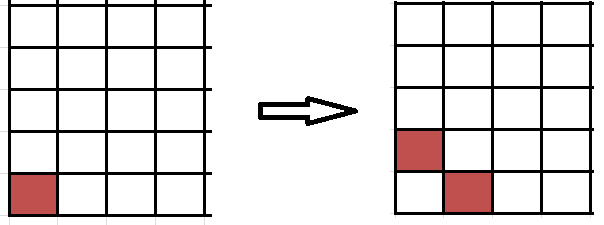
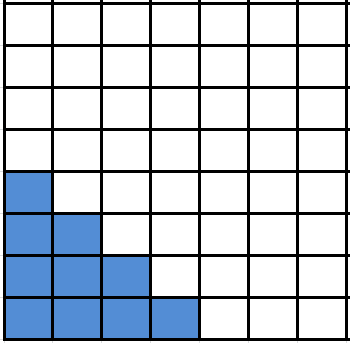
Suppose you have an infinite quarter-chessboard (ie, the chessboard extends infinitely far to the right and upwards, but not infinitely far down or to the left). Place a single checker on the bottom left square. On any turn, you are allowed to choose any checker on the board, remove it, and replace it with two other checkers: one above and one to the right of original checker (see the first image below). Is it possible to remove every checker from the 10 squares closest to the bottom left corner (the blue squares in the second image below)?


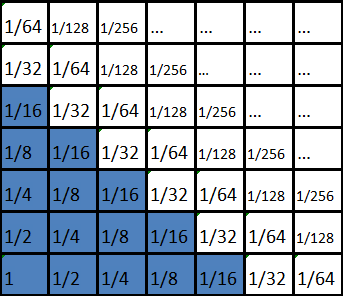
After some discussion we found that the answer was no - it is impossible to vacate the 10 blue squares. We proved this by cleverly choosing numbers to write in each square so that the sum of all of the numbers covered by the checkers was always 1, regardless of how many moves we have made (see the image below). We found that the sum of all of the numbers on the infinite board is 4 and noticed that the 10 blue squares total to 3.25. From this we proved that it is impossible to move the checkers around in a way to vacate the 10 blue squares.
After solving this problem we discussed how we would go about writing our solution down. The BAMO is a written exam - it is just as important to record your solution in a convincing and concise fashion as it is to solve the problem correctly. I strongly encourage you to try writing down the solution that we came up with in class. If you would like, Jonah and I are happy to discuss your written solution.
The second half of class was dedicated to continuing our discussion from last week about different ways to count votes. Last week we identified several different ways to choose a best candidate given how every voter ranks all of the candidates (for a summary, see here); this week we discussed ways to determine which of these approaches were "good." We came up with and named several criteria fora "good" vote-counting approach:
After coming up with these (fairly reasonable) criteria for a "good" voting system, we checked off which of our voting methods satisfied which criteria. We didn't quite finish our discussion and will continue it during our next meeting, but it was already clear that none of our voting methods satisfied all of the criteria above. So the question of "what is the best way to choose a candidate given everyone's votes" is still unanswered! (Think about how people vote around you - which of the above criteria do our voting methods satisfy?)
This week we started a new topic that we will be pursuing for the next few weeks: voting. We started by asking every student how they rank three different kinds of chocolate: white, dark, and milk, and then asking the simple question "which one is the best?" Here is the data that we collected in class:
| 4 | 5 | 4 | 3 | 9 | 1 |
|---|---|---|---|---|---|
| White | White | Dark | Dark | Milk | Milk |
| Dark | Milk | White | Milk | White | Dark |
| Milk | Dark | Milk | White | Dark | White |
This table represents that 6 people think that ranked white chocolate as their favroite, followed by dark and milk, 5 people chose white over milk over dark, etc. Now the question is "how do we choose which kind of chocolate is the best?" We came up with four different approaches to answering this question:
Clearly, there are many ways to pick which kind of cholocate is "the best," and different methods often led to very different results. We went on to discuss a few different ways to tell if a voting method was "good," and these kinds of questions are discussed more in the "things to think on" document for this week.
Welcome to the New Year! We started our first lesson with a fun one-day conversation about what we called "figures" (often mathematicians call these graphs). I won't go into all of the details of what we proved, but below is a brief summary.
Our "figures" were made up of "nodes" and "pathways" - pathways connect pairs of nodes. Whenever some area of a figure is enclosed on all sides by pathways we call the area a "region". We call a figure "flattened" when we can draw it on a piece of paper so that none of the pathways cross.
[Often mathematicians call "figures" graphs, "nodes" vertices, "pathways" edges, and "regions" faces]
We were able to show, in a somewhat hand-wavy fashion, that in a flattened figure the number of nodes (N) plus the number of regions (R) equals two plus the number of pathways (P): N+R=P+2. This famous result is known as Euler's formula.
We looked at many examples of figures such as the utility graph and several examples of complete graphs, finding that neither the utility graph nor the complete graph with 5 nodes can be flattened. We then showed that if we connect the right side of our paper with the left side (so that a pathway travelling off the left edge re-appeared on the right edge) and similarly connected the top to the bottom, then both the utility graph and the complete graph on 5,6, and 7 nodes can be flattened.
I encourage you to think about a few things at home:
a) Our proof of the N+R=P+2 formula was a little bit hand-wavy: try to make it a bit more rigorous. Think about taking some figure and steadily decreasing the number of regions by cleverly removing pathways. Find an invariant - something that is conserved every time you remove an edge (hint: it has to do with the formula N+R=P+2).
b) Clearly, our N+R=P+2 formula does not hold for figures drawn on paper where we connect the right/left and top/bottom edges. In class we hypothesized that a similar formula holds instead: N+R=P. Try to rationalize or prove this!
I hope you enjoyed this fun topic - there is much more to say about figures living on sheets of paper connected in various ways, and very much more to say about figures in general. Perhaps we will return to our study of figures in the future, but next week we will start a new topic.
See you all next Thursday!
PS: Based on the same principle as drawing figures on paper with the right/left and top/bottom edges connected is a fun game known as torus chess. I encourage the chess enthusiasts to try it out!
This week we started a new topic: counting! We started class by counting the number of ways to write some number n as a sum of 1s and 2s. Interestingly, we found that the number of ways to do this is the nth Fibonacci number, fn. We then show that this problem is identical to the following:
How many ways are there to tile a 1xn board with 1x1 and 1x2 tiles?
Since tiling will be a prominent source of discussion for the next few lessons, we showed (independently of our solution to the identical first problem) that there are fn ways to tile a 1xn board with 1x1 and 1x2 tiles. Here is our approach:
Let's denote the number of ways to tile a 1xn board as Tn. Notice that T0 = 1 (there is one way to tile a 1x0 board - and that is to not tile it), T1 = 1, and T2 = 2. Now, consider some n; let's look at the last square of an 1xn board. There are exactly two possibilities: either the last square is covered by a 1x1 tile or a 1x2 tile. If the last square is covered by a 1x1 tile, then (n-1) squares remain to be tiled, and there are Tn-1 ways to do that. If the last square is covered by a 1x2 tile, then (n-2) squares remain, so there are Tn-2 ways to tile the remaining squares. Thus, we find that there are Tn-1 + Tn-2 ways to tile a 1xn board, meaning that Tn = Tn-1 + Tn-2
Hopefully, you recognize this relation as the defining relation of the Fibonacci sequence (if you've never heard of Fibonacci numbers, I strongly encourage you to spend some time on Wikipedia and Google). Since T0 = f0 = 1, T1 = f1 = 1, and the recurrence for the T's and the f's are the same, we find that Tn = fn for all n. We saw several other interesting examples of how sums and products of Fibonacci numbers arise in tiling problems, the homework will be all about this!
If you would like to learn more about the machines that we have been studying, I invite you to browse the web. In class we have been giving these machines names like "choice machine" or "regular machine" etc, but there is a more accepted terminology that is described below. If you want to research these machines further make sure you search for these keywords:
I hope you have all enjoying learning about machines. Please let Jonah or myself know if you have any questions or comments! If there are any topics in Mathematics that you would like to learn about, Jonah and I welcome suggestions!
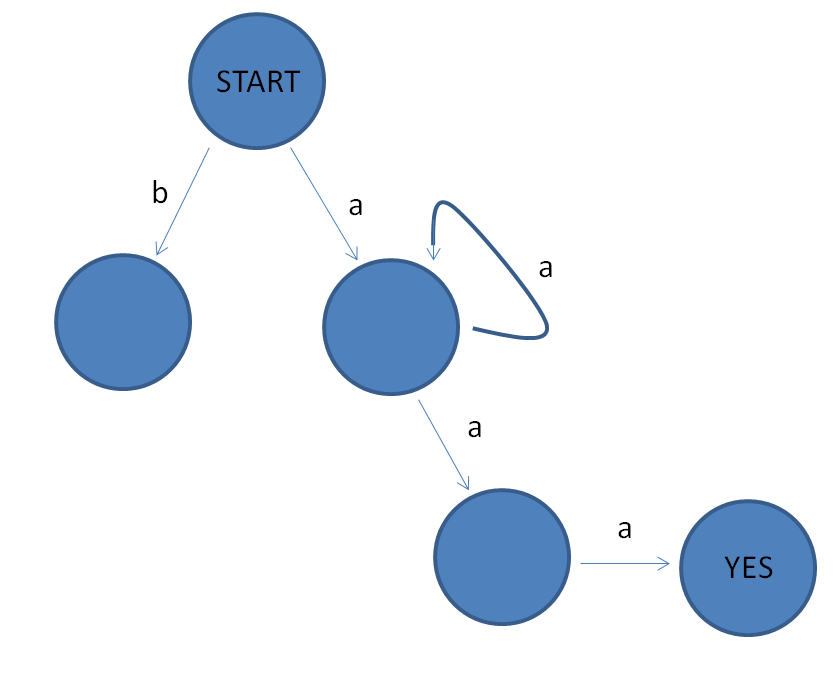
Our new choice machines do not have this restriction. Now, each node may have more than one arrow for a given letter. An example choice machine is below; notice that one of the nodes has two arrows with a. When we reach such a node, we can choose which arrow to follow. If for a given word there exists a way to choose your path so that you reach a "YES" node, then the word is accepted. If the next letter in your word does not have an arrow to follow (many of the nodes in the example are missing b arrows) then this current path is rejected. If there does not exist a way to choose a path so that you reach the "YES" node, the word is rejected. For instance, the word "ab" is rejected, as is "aab" and "abaab" (with "abaab, it is possible to choose a path for "abaa" that ends on the YES node, but then the final "b" causes this path to be rejected). In the example below you can show that only words that start with an a and end with two a's will be accepted.
We spent much of class using choice machines to learn more about for what kinds of words sets we can design machines. Our observations and conclusions are listed at the top of the homework (we actually didn't through all of them, but you can take them for granted if you wish to use them in the homework).
The homework can be found by clicking on the 2nd Year link above. Please work on it! It will help you tremendously to have thought about the homework before class! Especially pay attention to number 3 - it is the foundation for a very important theorem that we will discuss at some length next class.
Can we design a machine for any operation? Do there exist rules that would require an infinitely large machine to implement?
After much discussion, we found that the following problem will always require an infinitely large machine (infinitely large just means infinitely many nodes):
Design a machine that takes as input a word consisting only of the letters 'a' and 'b', and says 'yes' if and only if the word has the form of n a's followed by n b's. For instance, the machine will say yes to:
(empty input, n=0) ab (n=1) aabb (n=2) aaabbb (n=3) ...
The key to understanding why this problem would require an infinitely large machine is to notice that each possible value for n requires its own node. This can be proven as follows. Suppose that two sequences, one of k a's and another of j a's led to the same node N. Then, standing on N, there would be no way to differentiate between the j a sequence and the k a sequence. Notice that to get a 'yes' for the j a's we would need j b's, and to get a 'yes' for the k a's we would need k b's - this requires that we be able to differentiate between the two words that brought us to node N. Since we can't make this differentiation, it is impossible for the machine to give a yes for both the case n=j and n=k and exclude words like j a's followed by k b's or k a's followed by j b's. Therefore, every unique n must yield a unique node N corresponding to a sequence of n a's. Since there are infinitely many possible n, we find that there must be an infinite number of nodes.
Please note! Someone raised an excellent question in class:
Of course this machine requires an infinite number of nodes! There's an infinite number of possible words - any combination of a's and b's - and we need to say 'yes' to an infinite number of these (all possible values of n). It's no surprise that the machine has to be infinite!
Excellent thought, but it is incorrect. Recall, for instance, the divisibility-by-three machine that we discussed a week ago. This machine also accepted as input infinitely many "words" (strings of digits) and had to say 'yes' to infinitely many of them (all that were divisible by three), and yet we were able to successfully build a machine out of just three nodes! There is clearly something more complicated at play here, and we'll continue to discuss this question during our next meeting.
You will find a similar problem on this week's homework - I encourage you to apply similar logic to solve it! Please work on it!
This week we learned about a certain kind of machine which takes as input a (possibly nonsense) word and yields as output either a "yes" or a "no". The machine consists of a network of nodes (one of which is marked as the start node, and some of which are labeled as "yes" nodes) connected by arrows (which are labeled by letters). We use this machine by beginning at the start node and following, in order, the arrows corresponding to the letters of the word. Once we're done following all the letters of the word, we get a "yes" from the machine if and only if the node we end on says so. In this way, the machines allow us to tell whether or not the word follows a certain rule.
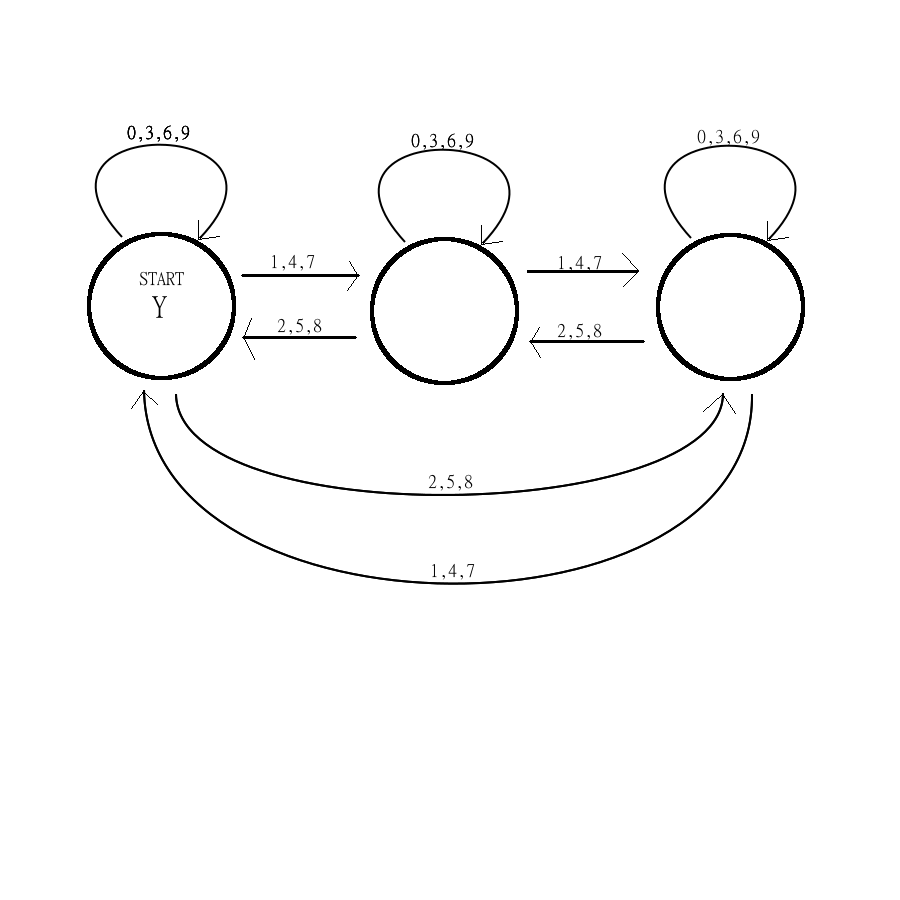
We looked at a lot of examples. Attached is a machine that only accepts "words" consisting of the digits 0-9. The machine says "yes" if the word represents a number that is divisible by 3 (or if there is no word). For instance, "0", "21", and "123" will all move you to the "Y" node, while "13" or "91" will not. The key to understanding how this machine works is to notice that you can only be in the leftmost node if so far, you have read in a number that is divisible by three. You can only be in the middle node if so far, you have read in a number that has remainder 1 when dividing by 3, and you can only be in the rightmost node if so far, you have read in a number that has remainder 2 when dividing by 3. Recall that a number is divisible by 3 if and only if the sum of its digits is divisible by 3. Try a few different words and make sure you understand how this works!
The homework is all about understanding how machines work and how to design machines to preform a specific operation. The last problem is especially important and we will discuss similar problems at length next week - please make sure you spend some time on it!
This Thursday we learned (for some, reviewed) a very powerful tool that is useful for solving many problems in mathematics: invariants. An invariant is some aspect of a math problem that doesn't change under the conditions of the problem statement. We looked at many examples, but I think the one that best exemplifies the power of invariants is the following:
Steve has 1001 stones in a pile. Every minute he is allowed to remove one stone from any pile, throw it in a nearby lake, and split the remaining stones in this pile into two new piles (each pile must have more than 0 stones). For example his moves might be:
1001 500 500 (picked the first and only pile) 123 376 500 (picked the first pile) 123 1 374 500 (picked the second pile) etc
Is it possible for Steve, after many iterations, to end up with only piles of three stones?
We spent a fair amount of time discussing potential approaches to this problem, but the most elegant that we came up with was to notice one fact: the sum of the number of stones in the piles plus the number of piles never changes. Before his first move Steve has 1 pile with 1001 stones (sum: 1002). On the second he has two piles of 500 (sum: 2 + 500 + 500). On the third, 123 + 376 + 500 + 3piles = 1002. It is straightforward to show that this must always be the case, no matter how Steve splits the piles.
Now, suppose that it is possible for Steve to end up with only piles of three stones. Then he would have n piles, each with 3 stones. Thus our sum would be 3*n + n = 4n (total number of stones plus number of piles). Since our sum can't ever change due to Steve's actions (it's invariant), this means that 4n must equal 1002. But 1002 is not divisible by 4, so we find that n cannot be an integer. Since n represents the number of stones, this shows that it is impossible for Steve to end up with only piles of three stones.
When solving problems using invariants it is important to first find an invariant (something that doesn't change) and then show that this invariant is different in the initial state (1 pile of 1001 stones) and in the final state (n piles of 3 stones). This implies that it is impossible to get from the initial state to the final state.
Attached is our first homework (it's all about invariants!). We will discuss these problems at the beginning of class so please try every problem (it's okay if you don't solve them - but it is important to have worked on them before we discuss).