cos(z)

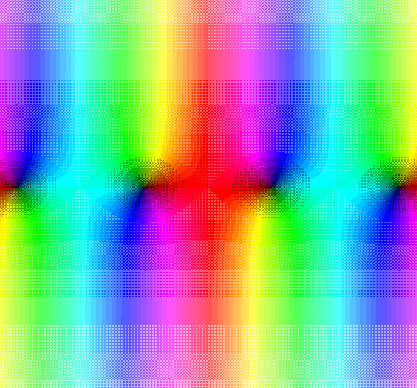
Here is the picture of cos(z). Note the vertical red and cyan (light blue) lines which correspond to the places where cosine is positive and negative. The distance between successive red vertical lines is the period. Notice also how cos(z) increases in modulus as the imaginary part of z increases. This function is best understood as the composition of (z+1/z)/2 and e^z and the rotation iz.

cos(z)=(exp(iz)+exp(-iz))/2 So perhaps a better way to illustrate this function is to note that vertical strips of width 2\pi are first rotated to horizontal strips of width 2\pi, then mapped to circles and rays (the standard plane), and finally mapped to ellipses and hyperbolas. Each of these three latter pictures is in the collection of pictures referenced on the Math 534 home page. What does the picture for cosh(z) look like? (rotate) What does the picture for sin(z) look like? (use sin(z)=cos(pi/2-z).)