Back to Math 445 Home Page | Back to Assignment Page | Next Assignment
Reading
Bix, Section 13, including some of the problems.
Handout from Geometry Turned On.
Bix, Sections 4 and 5 give an alternate view of the Euler line
and the Nine-Point Circle.
Also, see the Study Outline for Week 1.
Assignment A from Lab (Due Friday, 1/8/99)
Bring to class the following constructions, using figures that
will be handed out:
1. Construct the image of a point by a dilatation using parallel
lines, given a segment and its image.
2. Solve the square-inscribed-in-triangle problem.
3. Given two circles, construct the centers of similitude and
the common tangents.
4. Given angle ABC and a point D inside this angle, construct
all circles through D that are tangent to rays BA and BC.
Assignment 1: (80 Points, Due Monday, 1/11/99)
1.1 Inscribed Circles and Dilations (10 points)
Given two circles c1 and c2 inscribed in angle ABC, if c1
has center O1 and radius r1 and if c2 has center O2 and radius
r2, find the dilation D, with center B, that takes c1 to c2. What
is the ratio? Prove that D takes c1 to c2. (What must you prove?)
1.2 Midpoints and Other Points on a Line (20 points)
(a) Suppose a similarity transformation F takes segment AB
to segment CD. Prove that F takes the midpoint M of AB to the
midpoint N of CD.
(b) Also prove that for P = (1-t) A + t B, then F(P) = (1-t) C
+ t D.
(c) Let ABCD be a trapezoid, with AB parallel to CD. Let E be
the intersection of BC and AD and let F be the intersection of
AC and BD. Use the theory of dilations to prove that the midpoints
M and N of AB and CD lie on line EF. (Mention any special cases.)
1.3 Quadratic Bezier Curves (10 points)
Given a segment AB and a point P on line AB, if P = (1-t)
+ tB, then t is called the affine coordinate of P with respect
to A and B (the order of A and B is important).
(a) Suppose we are given three points A, B, and C and a number
t. Then let D be the point on AB with affine coordinate t and
E be the point on BC with the same affine coordinate t. If F is
the point on DE with the same affine coordinate t, find an expression
for F in terms of A, B, and t.
(b) If A = (1,1), B = (2,3) and C = (0,4), what is a formula for
F in terms of t?
1.4 Dilation in Coordinates (10 points)
Suppose that F is the dilation with ratio 30 and center (1,
2). If A = (2, 3) and B = (6, 7), what is F(M) if M is the midpoint
of AB? (The answer should be the numerical coordinates of a point.
Show your work.)
1.5 Ratios and Dilations (15 points)
(a) Given two circles with radii r1 and r2 and centers O1
and O2, let the external center of similitude be E and the internal
center of similitude be I. What is the ratio EO1/EO2 in terms
of r1 and r2? What is the ratio IO1/IO2 in terms of r1 and r2?
(b) What is the ratio (EO1/EO2)/( IO1/IO2)?
(c) In the theory of the nine-point circle, if the circumcircle
of triangle ABC is c with center O, and the nine-point circle
is b with center T, then the two centers of similitude are the
centroid G and the orthocenter H. What does this say about the
ratios GO/GT and HO/HT?
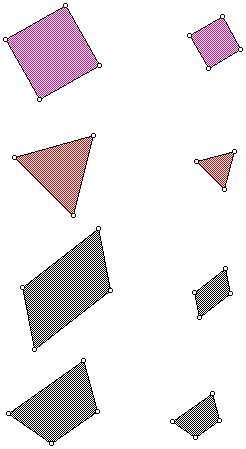
1.6 How many centers of similitude? (15 points)
(a) Given below are several pairs of figures. In each case,
construct the centers of similitude. What pairs have only one
center and which have two?
(b) What property must a figure have so that a figure and a dilation
of it must have two centers of similitude?
(c) Prove that your answer to (b) is true. Hint: Composition of
dilations.

Back to Math 445 Home Page | Back to Assignment Page | Next Assignment