Constructing Circles from Reflections – on the E plane, the D plane, the sphere and other spaces
We have defined the circle with center A through B as the set of points P so that the distance from A to P equals the distance from A to B. However, we can modify this definition slightly to avoid using distance measure.
Definition: The circle with center A through B as the set of points P so that the segment AP is congruent to the segment AB.
This means the same in the context of the Euclidean plane with a distance measure, but it now can be used in situations where we can compare two segments and check congruence but where we may not necessarily have a measurement of distance.
For example, in Dr. Whatif's Euclidean Geometry (DWEG), we say that a segment AB is congruent to a segment CD if there is a product of D-line reflections that takes A to C and B to D. (Recall that reflection in a D-line is circle inversion when the D-line is an E-circle. It is line reflection when the D-line is an E-line.)
Of course in the ordinary Euclidean plane it is true that AB is congruent to CD if there is a product of D-line reflections that takes A to C and B to D. This was a fundamental theorem about isometries proved in 444.
So how can this idea be used to construct a circle?
The Euclidean Construction
|
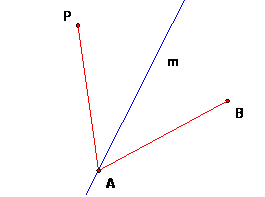
Begin in the (ordinary) Euclidean plane. Start with points A and B and let c be the circle with center A through B. Let m be any line through A. Let P = the reflection of B in m. Since m passes through A, the reflection of A in m is A. Thus AP is congruent to AB, and so P is on the circle c |
|
|
If we let m vary among the lines through A, the point P will also vary, but P will always be on the circle c |
|
|
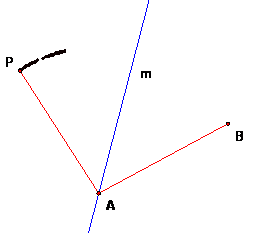
Conversely, if P is on the circle, then BAP is an isosceles triangle. Let m the line bisecting angle BAP. Then m passes through A and the reflection of B is P. Thus the points of c are exactly the set of reflections of B by lines m through A. |
|
.The DWEG Construction of a D-circle by reflection
The logic of construction is exactly the same. But the figure looks different from the Euclidean point of view.
|
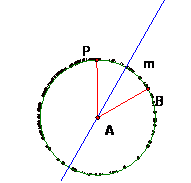
Begin in the D-plane. Start with points A and B and let c be the D-circle with center A through B. We will investigate the points of c. Let m be any D-line through A. Let P = the D-reflection of B in m. Since m passes through A, the reflection of A in m is A. Thus AP is D-congruent to AB, and so P is on the D-circle c |
|
|
If we let m vary among the D-lines through A, the point P will also vary, but P will always be on the D-circle c |
|
|
Conversely, if P is on the D-circle, then BAP is an isosceles triangle. Let m the D-line bisecting D-angle BAP. Then m passes through A and the reflection of B is P. Thus the points of c are exactly the set of reflections of B by D-lines m through A. |
|
Conclusion 1
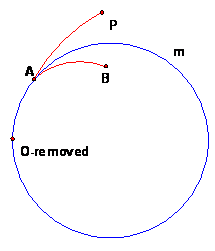
(D-circles are Apollonian circles): The
set of points in c viewed as a set in the E-plane is just the Apollonian circle
through B with respect to O and A. The
reason for this is that the Apollonian circle is orthogonal to all the
E-circles through O and A (i.e., the D-lines through A) and so the inversion in
any E-circle that is a D-line through A inverts the Apollonian circle to
itself, so inverts point B to a point on the Apollonian circle. Special case: If these Euclidean distances are equal:
Conclusion 2 (practical construction): To construct the D-circle, the simplest construction of the Apollonian circle intersects with E-line OA the interior and exterior angle bisectors of angle B in E-triangle OBA. The intersection points form an E-diameter of c. (See Ogilvy).