
In this worksheet, first we see why a circle (not through the center of inversion) inverts to another circle. Then we see that angles between circles (or circles and lines or lines and lines) are preserved by inversion. This work should be accompanied by a reading of Ogilvy Chapter 3.
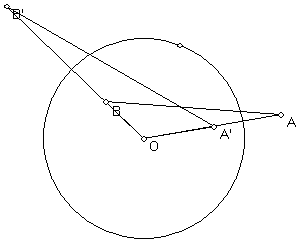
If points A and B are inverted in a circle c with center O to get A' and B', then triangle OAB is similar to OB'A'. (This was proved in 444 and will appear again in the homework.) Given this fact, mark the equal angles in these 2 figures:
|
|
|
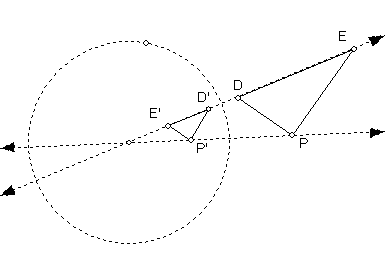
We want to prove if d is a circle that does not pass through O then the inversion of d is also a circle. We will do this starting from a diameter DE of d and a point P on the circle so that angle DPE is a right angle. The diameter DE is a segment on the line of centers of c and d. In other words, O is on line DE.
In each of the following figures, angle DPE is a right angle, mark the angles DEP and EDP and then mark the other angles in the figure equal to those. What is the sum of angles DEP and EDP? Can you deduce the measure of angle D'P'E' in each case?
Since P is any point on the circle with diameter DE, we can conclude that P' is always on the circle with diameter D'E'. This means that the inversion image of d is a circle. Why?
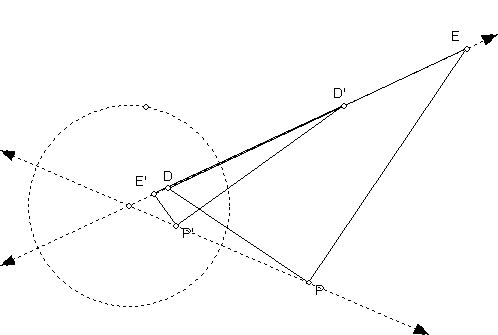
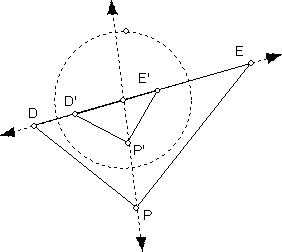
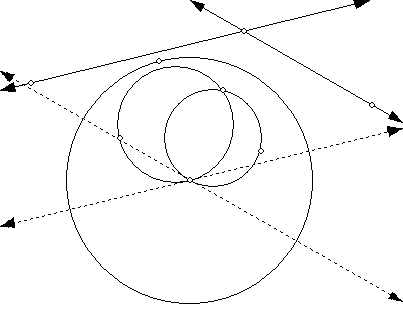
Suppose two lines are inverted in a circle. Explain from this figure why the images of the lines meet at the same angle as the original lines. Now we add to the first figure two circles tangent to the two lines. Why do they meet at the same angle also?

Above, we saw that when E, F and O are collinear and angle EPF is a right angle, then the inversion in a circle with center O of E, F, P to E', F', P' produces a right angle E'P'F'. HOWEVER, the triangle EPF is not similar to triangle E'P'F' (or F'P'E'). Just the right angle is the same. Also, the image of a side of triangle EPF is not a side of triangle E'P'F', For example the segments EP and FP become arcs of circles.