This lab will use a Sketchpad file called lab10.gsp that you can download here.
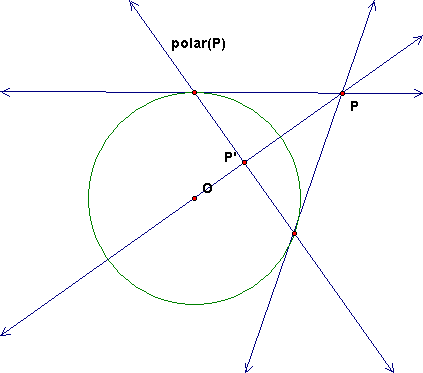
Given a circle c with center O and a point P, there is a special line called the polar of P. This line is defined to be the line perpendicular to line OP and through P', the inversion of P in c. When P is outside the circle, this line also passes through the points of tangency of the tangents to the circle through P, as we saw in one of the construction methods for inversion..

Question Important Later: For what point(s) is the polar the line at infinity?
Make a tool that constructs the polar of P from P'. It should work for P outside, inside and on the circle. You can use the inversion tool in lab10.gsp to construct P' and then work from there.Drag point P inside the circle to make sure your construction works there also. Also, if you merge P to the circle, then the polar line should become a tangent.
Step 1. In the lab file, on page Ex 1, there is already a figure P with two secants AB and CD add the other lines to construct UV and after dragging the points A, C, and P around to check on dynamic behavior, add the polar of P to see that it really is line UV. (The polar is the thick line in this figure.)

Step 2. Construct the intersection points of the polar with the circle and use these points to construct the tangents to the circle through P.
Experiment 1B. Construct the same figure starting fresh with a point P and a circle. Then construct the polar line of P and construct two points X and Y on this line. Then construct the secant lines PX and PY, the points A, B, C, D and see that the same figure results (with different points that can be dragged).
The pole of a line m is a point M. In fact it is the point M so that the polar of M is m. To construct the pole, just construct the point F on m so that OF is perpendicular to m. Then M is the inversion of F.
Make a tool that will construct the pole of a line. The givens should be the two points defining the circle and a "straight object", not 4 points.
This theorem states that given a circle c and a point P, the point Q is on the polar of P if and only if P is on the polar of Q.
We will use polars and poles to turn a circle d into a general conic section.
On page Exp3 in the lab files has been constructed a circle c and a circle d and also a point T on d and the tangent line t to d at T.
Now using your polar tool, construct the polar line T' of T in c. Then construct the Locus of T' as T varies. You will get the set of tangent lines of a conic section.
Hide your line locus. Now using your pole tool, construct the pole point t' in c of the tangent line t. Then construct the Locus of t' as t varies. You will get the set of points of a conic section.
To help you figure this out, return to your answer to the Important Question above. For what lines is the pole at infinity? This will tell you for a given d, for what t the poles are at infinity, which tell you the type of conic.
Note: This is really a projective transformation of the circle to the conic that produces quadratic equations for the curves. To see this, the clearest way is to write the transformation using coordinates. We shall not do this here.
Theorem: Given any six points A, B, C, D, E, F on a circle, the sides AB and DE, BC and EF, and CD and FA, are 3 collinear points.
On page Exp 4 in the lab files, carry out the instructions to construct the 3 intersection points and observe that they are collinear even in unusual and extreme arrangements on the circle.
A hexagon with the 3 intersections of opposite sides collinear is called a mystic hexagon.
If we take a projection of the circle figure in Experiment 4, we get Pascal's Theorem for a Conic. If we use poles and polars, we get the dual, called Brianchon's theorem.
On the page Exp5 is the same figure as in 4 but with a new circle and a conic defined as the locus of poles of tangents of circle d.
Use your tools to construct the polars and poles in c of these objects
How are these last 3 polars related? Does this work for ellipses, hyperbolas, etc.?
First we construct the sixth vertex of a mystic Pascal hexagon given 5 vertices and a line on which the sixth vertex is located. This translates into being given 5 vertices and 5 sides of a hexagon.
Next, we will use the dynamics of Sketchpad, to draw a conic. To do this, we will animate the line by attaching point J to a circle centered at E.
Now run the animation while you Trace point F. What does this look like? Now move some of your points A, B, C, D, E and clear trace and run the animation again.
Finally, replace the trace with a Locus (select F and J). Then you can hide J and its circle to make the figure look neater. In fact, you can hide everything except the 5 vertices ABCDE and the conic locus. Experiment with dragging the points around and see how the conic varies. You can even make a tool that constructs the conic from 5 points.