Geodesic Domes
This is taken from the website (http://www.peda.com/poly/poly.html) of Pedagoguery Software, which produces the Poly software. A trial version can be downloaded (registration appropriate for continued use).
"The first geodesic dome was designed by Walter Bauersfeld and was built in 1922. Several decades later, Buckminster Fuller popularized and extended the ideas behind geodesic constructions.
To construct a geodesic sphere, you first choose a convex polyhedron which will serve as a framework for the construction. The next step is to ensure all of the polyhedron s faces are triangular: each non-triangular face is triangulated by connecting its vertices to a new vertex placed at the center of the face. You will then have a 1-frequency geodesic sphere if all of the vertices are made to be equidistant from the center of the polyhedron by moving them directly away from or towards the center.
Higher frequency geodesic spheres may be constructed by replacing each face with a regular triangular mesh and then ensuring all of the new vertices are equidistant from the center. 2-frequency geodesics bisect each edge of their associated 1-frequency geodesics by using 4 triangles for each mesh; 3-frequency geodesics trisect each edge and add one vertex to the center of each face of their associated 1-frequency geodesic by using 9 triangles for each mesh."
2-Frequency Octahedral Geodesic
Sphere
This polyhedron is almost the same as the cuboctahedron, except that the square faces are divided into 4 triangles. This is the "midpoint" figure of the octahedron.
Cuboctahedron

2-Frequency Octahedral Geodesic
Sphere

3-Frequency
Octahedral Geodesic Sphere

Questions on Geodesic Domes
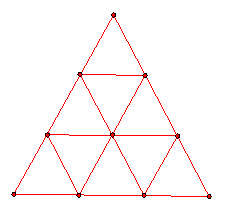
This 3-frequency octahedral geodesic dome is a polyhedron inscribed in a
sphere that obtained by subdividing each face of an octahedron into 9 congruent
equilateral triangles and projecting outward from the center.
1. If
AB is a chord of a circle with center O (but not a diameter), the ray
Suppose points P and Q are on the chord AB and trisect the chord AB, i.e. AP = PQ = QB. Let P' and Q' be the intersections of OP and OQ with the circle.
Do the rays OP and OQ trisect the angle AOB? Tell whether or not this is true and give a clear and convincing explanation and justification for your answer.
Extra Credit: You may have heard that "it is impossible to trisect an angle". Look up some information about this and write a paragraph or two, first giving a true and precise statement that clarifies the rather vague statement in quotes. Then add a bit about the history of the angle trisection problem and how it was eventually resolved.
2. Why
go to all this trouble to construct a geodesic dome with 72 triangular
faces. Why not just construct the dome
from about that many equilateral triangles.
Wouldn't that be simpler?
3. Consider the 3-Frequency octahedral geodesic dome based on an octahedron inscribed in a sphere of radius = R and center O. Assume that the octahedron is in coordinate 3-space and that the vertices of the octahedron are on the coordinate axes. Then a vertex P' of the dome is obtained by taking a vertex P from the plane triangle shown above and setting P' to be the intersection of OP with the sphere. We call this central projection from the polyhedron to the sphere.
a. Tell the coordinates of all 10 of the plane vertices in the figure above, assuming the vertices of the octahedral face are on the positive coordinate axes.
b. Tell the vertex angles and side lengths of all 9 of the triangles in the plane figure. Tell the areas of each of the plane triangles.
c. Tell the coordinates of all 10 of the points on the sphere obtained by centrally projecting the points in (a).
d. Tell the vertex angles and side lengths (in degrees or radians) of all 9 of the spherical triangles in the plane figure. Some triangles are congruent. Tell which triangles are congruent, whether any are equilateral, isosceles, etc. Tell the areas of each of the spherical triangles.
e. [Ignore this point and do not answer it. It was left on the left by an editing error. It duplicates (c) and (d).] Tell the vertex angles and (spherical) side lengths of the spherical triangles obtained by dividing a face of the octahedron as above and constructing vertices on the triangle by projecting the planar vertices out from the center of the sphere to the surface of the sphere (i.e., for a vertex P on the plane, let the vertex P' on the sphere be the intersection of OP with the sphere).
f. The vertices of each spherical triangle also form a plane triangle inscribed in the sphere. Compute the vertex angles and the edge lengths of the sides of each of the 10 inscribed plane triangles that have the vertices of the 10 spherical triangles in (d). These are the triangles that form the polyhedron that is the geodesic dome!