4. Explain what is meant by a pencil of circles. Tell what are the 3 kinds of pencil. Explain why any two circles belong to a unique pencil and why the circles orthogonal to these circles form a pencil also. Show and explain how to start with two given circles and a point P and construct the circle through P that is in the pencil containing the two circles -- do the cases of circles intersecting in 2, or 1, or 0 points.
A pencil of circles is another name for specific families of circles who all share certain characteristics within the family.
An elliptical pencil of circles is the family of all circles that go through two given points. This is why another name for them is a two-point pencil. These circles are all intersecting, but never anywhere but these two points.
A hyperbolic pencil of circles, also called Apollonian circles, is the family of all circles that are orthogonal to the set of circles that go through 2 given points. Thus, the elliptical pencil of circles always has a corresponding hyperbolic pencil of circles that are orthogonal to every circle. None of the circles in the hyperbolic pencil intersect with each other, thus they are also called the zero-point pencil.
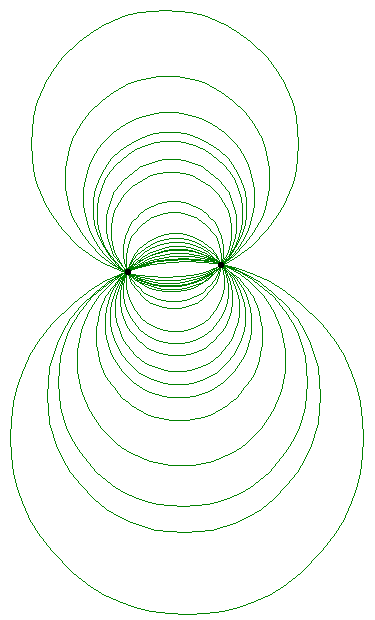
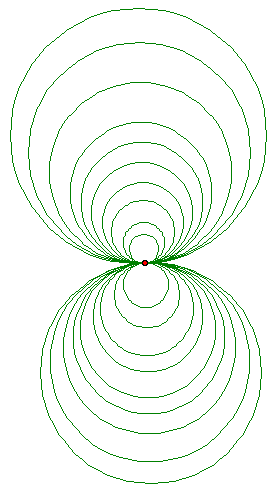
The third kind of pencil is the parabolic pencil. This is the family of circles which all have one common point, and thus are all tangent to each other, either internally or externally. Also, the orthogonal set of circles to a parabolic pencil is another parabolic pencil.

