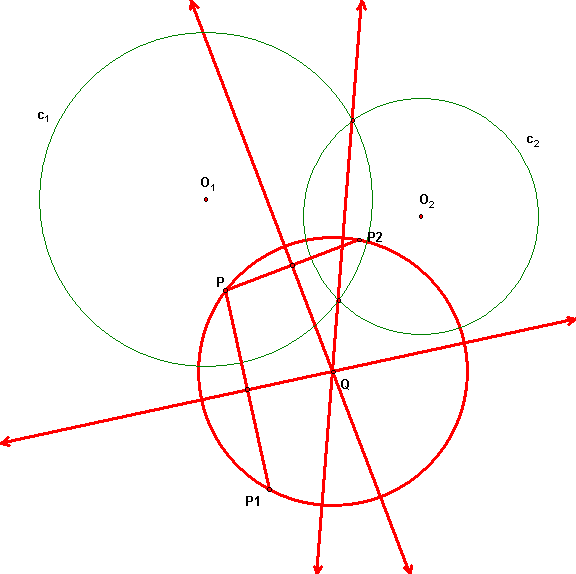
Problem 1. Construct with straightedge and compass the circle through point P that is orthogonal to circles c1 and c2. (The centers of the circles are O1 and O2.) WRITE BRIEFLY the main steps of your construction. You do not have to justify the steps, just make it clear what you did.
Answer: To find Q, the center of the orthogonal circle, you need to intersect two lines (two radical axes). Two of these radical axes can by constructed by inverting P in each circle and constructing the perpendicular bisector of P and its inversion. This constructs the circle as the circumcircle of P and its two inversions. This is correct and OK.
But in this particular figure there is a short cut: the radical axis of c1 and c2 also passes through Q (always), but in this case that radical axis is simply the line through the two intersection points of c1 and c2, so it is easy to construct just by drawing this line. Then you only need to construct one of the remaining two lines. (Info on construction if inversions of points on class handout 2/19 and all the reading.)
Some students used a variation and inverted P in O1 to get P' and inverted P' in O2; then constructed the circumcircle of these 3 points. This is fine also.

Problem 2. In this figure, line ED is tangent to the circle.
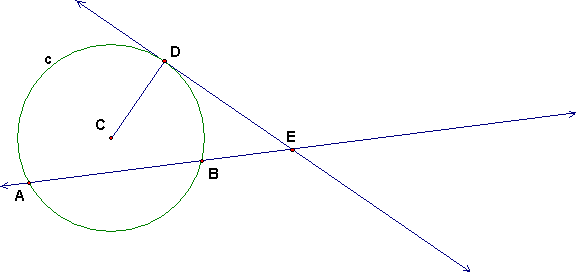
(a) What is the radius of the circle d centered at E that is orthogonal to circle c?
Answer: ED.
(b) Draw this circle into the figure as accurately as you can.
Answer: Draw circle with center E through D.
(c) State precisely what it means for these two circles to be orthogonal.
Answer: Given that D is a point of intersection of the two circles, it means that angle EDC is a right angle. Another way to say this is that the radius ED of circle d is tangent to c at D
(d) State precisely what it means for A to be the inversion of B in circle d.
Answer: Since B is on ray EA, if R = |ED| is the radius of the circle, it means that EA EB = R2 = ED2.
(e) Explain why, if circle d is orthogonal to circle c, that B must be the inversion of A in d. (You can quote needed theorems, except for this one, but state clearly definitions and "facts" that you use.)
Answer: Since the circles are orthogonal the radius ED is tangent to c at D. But by the theory of the power of a point, then EA EB = square of tangent length = ED2. Both numbers are equal to the power of the point E with respect to c. But by (d) this means that B is the inversion of A in the circle with center E and radius ED.
There were many ways to say this, but the KEY is this. You get one relationship for tangent lengths and then use the fact that orthogonality says the tangent length = radius to get the inversion relation. Otherwise, there were a lot of ways to subtly assume the conclusion.