Constructions from Three Theorems of Projective Geometry – Constructing with a Ruler -- an unmarked Straightedge

We will explore in class 3 theorems and related constructions in the projective plane.

  1. Complete quadrangle and polar line of a point
  2. Desargues Theorem – (in lab)
  3. Pascal's Theorem (and in lab the related variants of Brianchon and Pappus)

Review: The Complete Quadrangle

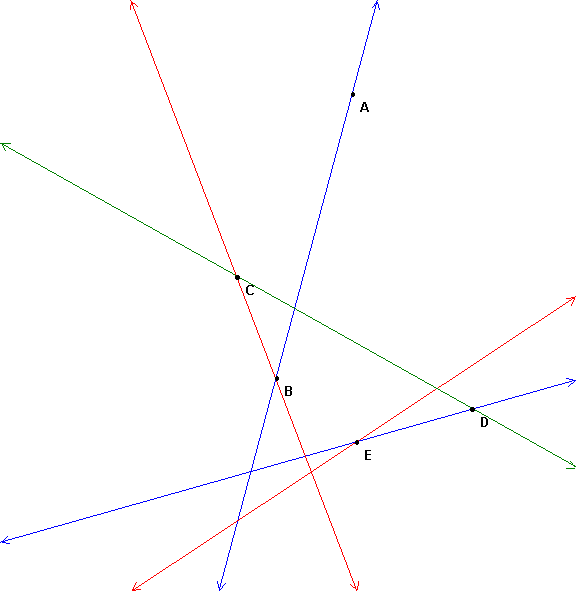
Draw 4 points in the plane (sort of randomly in the middle of this sheet of paper). Given 4 points ABCD draw the sides to form a quadrangle as usual.  But since inside and outside don't stay the same when figures are projects, draw ALL lines that connect pairs of these points.  This is called the complete quadrangle ABCD.  How many lines do you get?

Next label all the intersections of these lines (besides A, B, C, D).  If the lines of intersection lie outside the paper, you may want to try again or you can just think it through.  How many points?  These points are called diagonal points of the complete quadrangle.


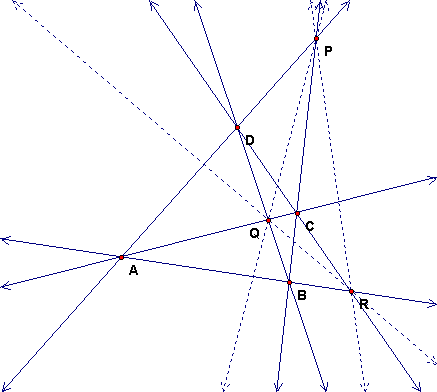
You should have gotten a picture kind of like this.  We have seen this figure before.  The first time was when we constructed harmonic sets with a straightedge and the second time was when we made a perspective drawing of two intersecting roads.

Mark point X as the intersection of line AB with line PQ.  We saw before that ABRX is harmonic.  Notice that there are also 4 points of intersection with lines on line RQ and line RC. These are all projections of ABRX with center P, so they are harmonic also.  Each of the 9 lines in the figure meets the other 8 lines in 4 points, and the 4 points are always a harmonic set.

Application of the complete Quadrangle to constructions with conic sections

Draw a point P somewhere below this ellipse and then draw two secants intersecting the conic at A and B for one and C and D for the other.  Then P is one of the diagonal points of ABCD.  Construct the other two diagonal points QR and line QR.  You will need to choose ABCD carefully so that the diagonal points are all on the page.

Pascal's Theorem

Draw the 6 lines that make hexagon ABCDEF.  Then label the points of intersection and look for a relationship.

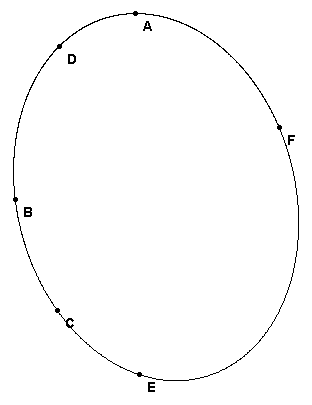
Here is another example to try out

Complete the Magic Hexagon

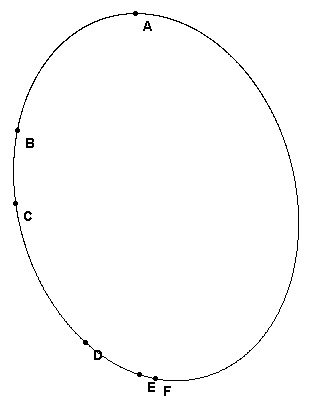
In this figurre are 5 vertices A, B, C, D, E and 5 lines. If the hexagon is a Pascal, or magic hexagon, with opposite sides intersecting in 3 collinear points, then it is possible, given 5 vertices and 5 sides, to find the sixth vertex and the sixth side to make a hexagon ABCDEF. It turns out that there is a unique conic through the 5 vertex points and the point F is also on the conic. E and F are the intersections of the fifth side with the conic.

Construct F in this figure.