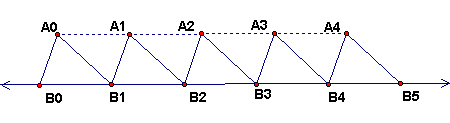
Refer to Sved Problem 4-2 for details about the figure below. In each case a row of congruent triangles is placed with bases on a line, so the vertices B0, B1, B2, …, Bn are equally spaced with b = BkBk+1 for any k. The distances A0A1 = A1A2 = … AkAk+1 .. are all equal to some length a. But in general a need not equal b as we will see below.

Suppose in each case that the figure is extended so that there are n triangles, so the bases vertices are B0, …, Bn. We also write the distances h = B0A0 and k = An-1Bn.
Let d = defect of triangle A0B0B1 = 180 degrees – angle sum. The defects of all the congruent triangles are the same.
Now consider the two angles p = angle B0A0B1 (peak angle) and v = angle A0B1A1 (valley angle). We can compare these angles.
In triangle A0B0B1, the angle sum =
angle A0B0B1 + angle A0B1B0 + p = 180 degrees – d.
The sum of the angles at B1 is a straight angle, so
angle A1B1B2 + angle A0B1B0 + v = 180.
Since angle A0B0B1 is congruent to angle A1B1B2,
angle A0B0B1 + angle A0B1B0 + v = 180.
This means that
p + defect = v.
If the defect = 0, as it is for Euclidean geometry, then p = v. Thus all the triangles are congruent and a = b. In this case, also the A vertices all lie on a line parallel to the line of the B vertices.
On the sphere or any other space with negative defect, the angle p. Then the angle p > angle u and thus side b > a. This looks something like the figure below.
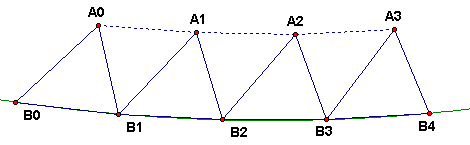
Now this figure can be used to show a contradiction to the assumption of negative defect in a geometry in which are valid the axioms of Euclidean geometry except for a parallel postulate (where in particular the lines have infinite length and the triangle inequality holds).
So assuming negative defect, one has b = a + e, for some positive e.
The path of segments from B0 to Bn via the A points has length |B0A0| + (n-1)a + |An-1Bn| = h + k + (n-1)a.
The (straight) line segment from B0 to Bn has length nb.
The contradiction occurs when n is so large than the path through the A's is shorter than the straight-line path. This happens if
h + k + (n – 1) a < n b = n(a + e), or h + k – a < na + ne – na = ne. So if n > (1/e)(h + k – a), the segment path is shorter, which contradicts the triangle inequality.
Thus it is impossible in such a geometry that the defect of a triangle can ever be < 0.
Refer to Sved Problem 4-3.
If AB = AC, then we know the sum of the angles if triangle ABC is = 180 (Euclidean) or < 180 (plane with defective triangles). We also know the sum of angles BAC and BAE. Find the relation between angle BAE and angle BCA.
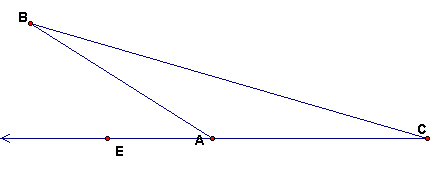
Start with ZA perpendicular to line AB and mark off BC = BZ. In the isosceles triangle ZBC, angle ACB < (1/2) angle ZBA. Continue indefinitely in this way. The next point is D on line AB so that CD = CZ. Then angle ZDC < (1/2) angle ZBC < (1/4) angle ZBA, etc. The a point Pn can be constructed on ray AB so that angle ZPnA < (1/2)n angle ZBA. In other words the angle in the triangle can be made arbitrarily small.
Continue as in Sved.
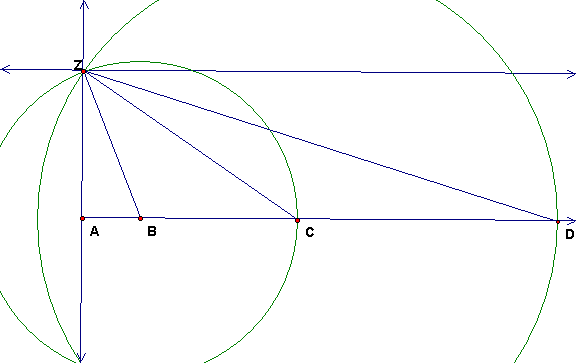
This is the proof in Berele-Goldman.
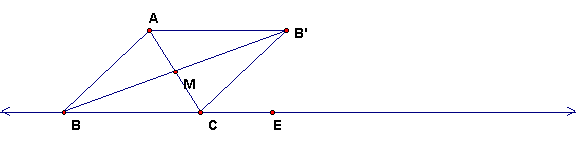
This figure can be used to prove the Exterior Angle Theorem. Triangle AB'C is obtained from ABC by point reflection in the midpoint of AC. Explain why the exterior angle ACE > angle ABC. From this conclude than an exterior angle of a triangle is greater than EITHER of the non-adjacent interior angles.
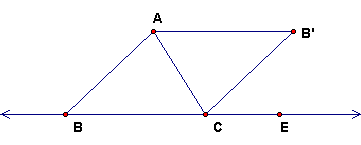
Also, conclude that the sum of any two interior angles of a triangle is < 180 degrees.
BG proof that defect = 0 or < 0 then uses the construction below of a triangle B'BC that has the same defect as ABC but one of the angles is half as big as the smallest angle in ABC. Continuing this halving, one can find a triangle with the same defect as ABC but with the smallest angle smaller than the defect. This means that the other two angles have sum > 180, which give a contradiction to the exterior angle theorem above