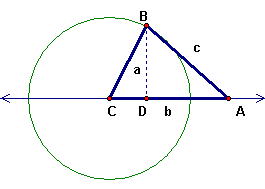
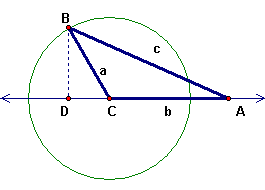
CD = a cos t
CD = a cos t (if CD is taken as negative)
|CD| = a |cost t| = -a cos t = a cos (180 - t)
BD = a sin t
BD = a sin t
AD = b - a cos t
AD = b + |CD| = b - a cos t
In the triangle ABC the side lengths are a = BC, b = CA, c = AB. The point D is the foot of the altitude through B. Let us call angle ACB = t. For each of these figures, write CD, BD, and AD in terms of trig functions of t and a, b, c.
|
|
|
|
CD = a cos t |
CD = a cos t (if CD is taken as negative) |CD| = a |cost t| = -a cos t = a cos (180 - t) |
|
BD = a sin t |
BD = a sin t |
|
AD = b - a cos t |
AD = b + |CD| = b - a cos t |
c2 = a2 + (b - a cos t)2
c2 = a2 + b2 - 2ab cos t
Suppose that A = (a1, a2, a3), B = (b1, b2, b3), C = (0, 0, 0). Use the algebraic distance formula to compute:
c2 = |AB|2 = (a1 - b1)2 + (a2 - b2)2 + (a3 - b3)2 =
((a1)2
+ (a2)2 + (a3)2) + ((b1)2 + (b2)2
+ (b3)2) - 2 (a1b1 + a2b2 + a3b3)
Write here what we found about the dot product and cosine
Rewriting the last equation, we give a name to the expression
(a1b1
+ a2b2 + a3b3)
and call it A.B, the dot product of A and B. The dot
product can be defined in n-space of any dimension. For two vectors, multiply
the corresponding entries and then add. In this case
c2 = a2 + b2 - 2A.B
Thus:
A.B = |A| |B| cos (AOB)
Notice that the square of the length is also a dot product of the vector with itself, so this equation can be written this way (with C = O having zero coordinates):
b2 = |OA|2 = A.A; a2 = |OB|2 = B.B; c2 = |A - B|2 = (A-B).(A-B)
This leads to the observation that the algebraic version of the Law of Cosines comes from the distributive law [A.(B+C) = A.B +A.C] and the commutative law [A.B = B.A] for dot product:
(A-B).(A-B) = A.A - A.B - B.A + B.B = A.A + B.B - 2 A.B
Suppose that triangle ABC is a spherical triangle with a right angle at C. We can choose space coordinates so that C = K = (0,0,1), A is in the (x,0,z) plane and B is in the (0,y,z) plane. Here are two cross-sections, with I = (1, 0, 0) and J = (0, 1, 0).
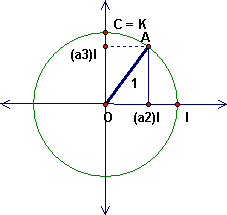
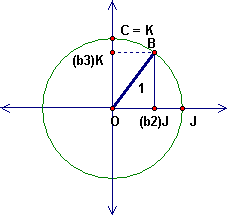
The spherical distances a = BC, b = CA and c = AB are actually angle measures. What are the angles in each case?
Using the angles a, b, c, what are the coordinates of A?
Using the angles a, b, c, what are the coordinates of B?
Now use the dot product to compute cos c. This is the "Pythagorean Theorem for the Sphere."
Since to measure c, we measure angle AOB, we can find the cosine of this angle from the dot product, as explained above.
|A||B|cos c = A.B
But since |A| = |B| = 1 (from the geometry or from the formula), then
cos c = A.B = 0 + 0 + (cos a) (cos b)
Then for a triangle with right angle at C, the Pythagorean Theorem for the Sphere states
cos c = (cos a) (cos b)
Remark: It is hard to recognize the usual Pythagorean theorem in this, but for very small angles t, cos t is approximately equal to 1 - t2/2. So this equation became an approximate equation (1 - c2/2) "=" (1 - a2/2) (1 - b2/2) "=" 1 - (1/2)(a2 + b2), so c2 "=" a2 + b2 (we ignore the a2b2 term and other fourth power terms since they are much smaller than the quadratic terms). Thus, "in the limit" the spherical formal agrees with the formula for the flat plane.