Stereographic Projection
This is an outline of the basic construction for stereographic projection and
a statement of some basic properties.
The central projection of 3-space from a point N to a plane onto
a plane F (not through N) is defined as follows:
- For any point P of 3-space, construct the line NE.
- Intersect the line NE with the plane F. The point of intersection
c(P) is the central projection of P to the plane with center N.
- Note: This projection is not defined if point P is on the plane through
N parallel to F.
The stereographic projection of a sphere E onto a plane F
from a center N is defined as follows.
- Point N must be on the sphere E and the plane must be perpendicular to the
diameter line of the sphere through N.
- For any point P of the sphere E distinct from N, construct the line NP.
- Intersect the line NP with the plane. The point of intersection s(P) is
the stereographic projection of P on the plane with center N.
- Note: This is the same as central projection of P but with domain restricted
to the sphere. From the way the center and the plane were chosen, the line
NP is never parallel to the plane for a P distinct from N, so the stereographic
projection maps the sphere – {N} to the plane.
- Note: Unlike the case of central projection from 3-space, there is an inverse
map from the plane to the sphere. For a point Q on the plane, construct line
NQ. This line intersects the sphere at N and also another distinct point
P (since the line is not tangent to E). This point P is the inverse stereographic
projection of Q.
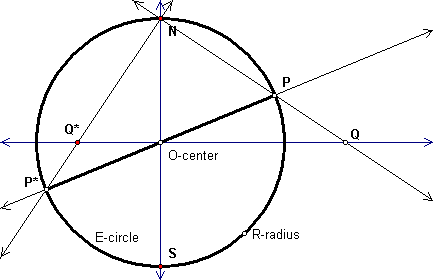
The figure below shows the stereographic projection from P to Q. The plane
F is through the center of the sphere (think N = north pole,
plane = plane of equator). It also shows the projection of the antipodal point
P* of P to Q*.
Properties of Stereographic Projection
Additional information about Stereographic
Projection from a point N on a sphere is given in the web references.
The properties of Stereographic Projection that we will use are these (we
have indicated a proof of (a), the other two will be proved in class).
(a) Stereographic
projection is a 1-1 map of the sphere onto the plane, except that projection
image of the projection center N is not defined (or may be set = infinity).
(b) Circles on the sphere
not through N map to circles on the plane. Circles through N map to
lines on the plane.
(c) Angles are
preserved by stereographic projection.

