Assignments for Week 5
Reading for Week 5.
Read the handout from DeVilliers on Proof.
Most of the new geometry this week will be on the topic of vectors and coordinates. Several handouts will contain the bulk of the reading. Read these handouts.
At the same time, we will continue with some exercises designed to keep up and increase skills in problem-solving and theorem proving in Euclidean plane geometry. This is a good opportunity to review B&B and read the chapters in B&B on Constructions and Loci.
Exercises 9 (Due Wed 10/27)
E9.1 Distances on rays OA and OB
Given points O, A, B, suppose that |OA| = a and |OB| = b, and that A' is a point on ray OA with |OA'| = 1/a and B' is a point on ray OB with |OB'| = 1/b.
If |AB| = c, what is |A'B'|?
Your answer should be in terms of a, b, c and you should give a brief but convincing proof.
E9.2 Altitudes as perpendicular bisectors
Let ABC be a triangle. Construct a new triangle A'B'C' so that line B'C' is the line through A parallel to line BC, line A'B' is the line through C parallel to line AB, line C'A' is the line through B parallel to CA.Exercises 10 (Due Friday, 10/29)
E10.1 A distance relationship
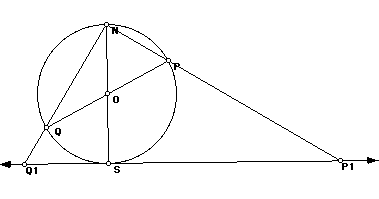
In the figure, the circle has center O and radius r. PQ and NS are diameters. Line P1 Q1 is tangent to the circle at S.
(N, P and P1 are collinear and also N, Q, Q1 are collinear, as they appear to be.) Problem: Find a relationship among the quantities |NS|, |SP1|, |SQ1|.

E10.2 Vector Exercises
Do all the exercises in 2.9 (p. 29) in the Farin handout. Some will be done in class.
Assignment 5 (80 points, Due Mon. November 1)
Problem 5.1 (15 points) Circumcenter of Isosceles
Given an isosceles triangle ABC, with |AB| = |AC| = b and |BC| = a, what is the radius of the circumcircle of ABC? (The answer should be in terms of a and b, if possible.)
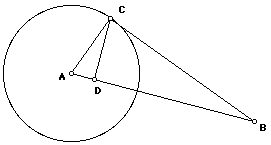
Problem 5.2 (10 points) Distance in a tangent figure
Given a circle with center A and radius r and also a point B exterior to the circle. Let line BC be tangent to the circle at B and segment CD be perpendicular to AB. Find and prove a relationship among AB and AD and the radius r.