This chapter contains the basic properties of parallel lines and transversals. It also introduces coordinates and the slope of a line.
In these proofs you can use the theorems in Chapters 1, 2, 3 of B&B. Also, for problems from Chapter 4 of B&B you can use theorems that precede in the book what you are trying to prove. You can also use what you yourself prove in the homework so long as you keep a logical sequence and do not end up with circular reasoning.
(a) For a quadrilateral ABCD, prove that the midpoint quadrilateral
of ABCD is a parallelogram. (Yes, this is a repeated of an earlier exercise.) (b) If ABCD is a kite, what kind of polygon is the midpoint
quadrilateral? Prove your assertion. (Note: In a
problem of this kind you should give the best or strongest possible
answer whether or not it is spelled out each time. For example, it is
true that the polygon is a parallelogram, but this is not a satisfactory
answer.)
Prove the following problems on B&B, pp 113-114. Important: Use
the definition of a parallelogram at the beginning of the Exercises on
p. 113. Do not use other equivalent definitions. For tools, you
can use anything proved in B&B through p. 122.
3.3 Rhombi (10 Points)
(a) A rhombus is defined to be a quadrilateral with four equal sides. Prove that a rhombus is a parallelogram.
(b) Prove that a parallelogram with perpendicular diagonals is a rhombus.
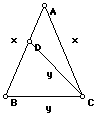
Let ABC be an isosceles triangle (AB = AC = x) and let D be a point on segment AB so that CD = CB = y.

(a) What are lengths BD and AD in terms of x and y?
(b) If triangle DAC is also isosceles (i.e., DA=DC), find the the ratio x/y.
3.5 Special Midpoint Quadrilaterals (15 points--or more for unusually good answers)
(a) Consider this statement: If the midpoint quadrilateral of quadrilateral ABCD is a rectangle, then ABCD is a kite.
Prove it if it is true. If it is false, give a counterexample and, if you can, explain for which quadrilaterals the midpoint quadrilateral is a rectangle.
(b) Consider this statement: If the midpoint quadrilateral of ABCD is a rhombus, then ABCD is a rectangle.
Prove it if it is true. If it is false, give a counterexample and, if you can explain for which quadrilaterals the midpoint quadrilateral is a rhombus.