Math 444 Quiz #2

Do both problems. The first is a construction and the second is a proof.

Link to Answers.

Problem 1 (20 points)

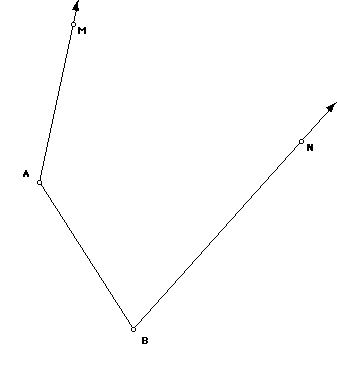
The figure below consists of the segment AB and two rays, ray AM and ray BN (with arrow indicators on the ends). Construct with straightedge and compass a circle which is tangent to all 3, the segment and both rays.

Instructions: As last time, label your construction and write a brief description of the steps. Just right enough to make it clear what you did, not why it works.

 

 

Link to Answer 1.

Problem 2 (20 points)

What you can use.

You can use any of the theorems from B&B Chapters 1-5 (this includes the recent chapter on circles). Don’t assume problems from B&B (especially this one!).

 

The Problem

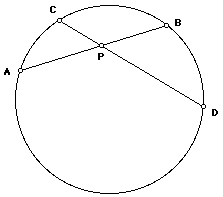
  1. Given two chords of a circle, AB and CD, which intersect at a point P, find a relationship among the four lengths PA, PB, PC, PD.
  2. Then prove that the relationship is true. Hint: Similar triangles.

 

 

 

 

 Link to Answer 2.

Answers to Math 444 Quiz #2

Answer to Problem 1.

Since the circle will be tangent to all three lines or segments, the center is equidistant from each, so the center is on both angle bisectors. Construct the center as the intersection of angle bisectors.

Then construct the radius by dropping a perpendicular to one of the sides.

 

 

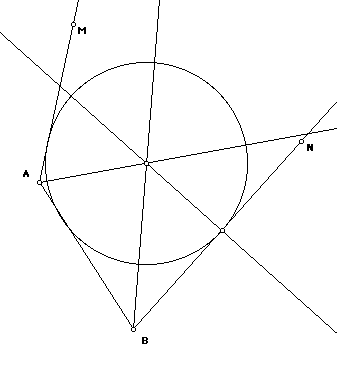
Back to Problem 1.

Answer to Problem 2.

Angles ACD and ABD are equal, since they are inscribed angles with the same arc. Likewise angle BDC = angle BAC. Since angle BAC = angle PAC, etc., we have triangle ACP is similar to triangle DBP by AA. (We could also have used for AA one pair of the inscribed angles and the vertical angles at P instead of the second inscribed angles.)

Note: If you draw different segments, you can show that triangle APD is similar to CPB in the same way ang get the same result. Either choice of triangles works equally well.

Thus by corresponding parts, PA/PD = PC/PB, or PA PB = PC PD.

 

 

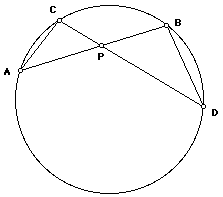
 Back to Problem 2.
Back to Math 444 Home Page