OUTLINE FOR MIRROR ACTIVITY.
Line Reflection and Perpendicular Bisectors
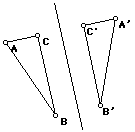
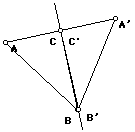
Definition of line reflection. Given a point A and a line m, let n be the line through A perpendicular to m. If N is the intersection of m and n, there is one point A’, distinct from A, so that |AN|=|A’N|. This point is called the reflection of A in m.
Another way to say this is that A’ is the unique point so that m is the perpendicular bisector of AA’.
Line Reflection is an isometry so preserves congruence.
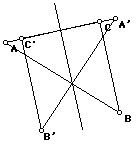
If A and B are points, and A’ and B’ are the reflections of A and B in line, m, then |AB| = |A’B’|.
Proof is by applying Pythagoras to this figure (several cases shown). This is equivalent to using coordinates (see B&B Chapter 4).


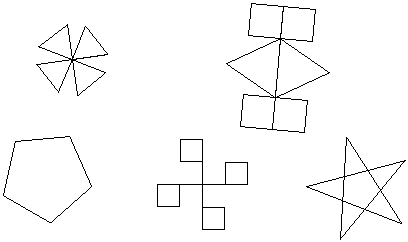
Line Symmetries
What are the line symmetries of these?