Math 444 Assignment 9 (70 points)

    1. Ratios in a triangle (10 points)

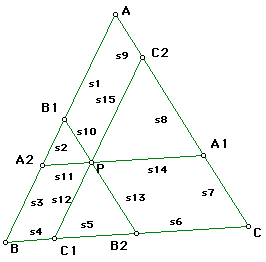
      2. The segments through P are parallel to the sides of the triangle.

      Let a = |BC|, b = |CA|, c = |AB|. Let x = CA1/CA, y = AB1/AB, z = BC1/BC.

      For the segments numbered s1-s15, deduce the lengths of the segments in terms of a, b, c, and x, y, z and then label the segments with the lengths.

      Use the fact that the lengths of shorter segments add up to the lengths of the longer segments, such as AB to find relationship among the ratios a, b, c. What is this ratio?

       

    2. Wallpaper symmetries (20 points)

      3. The instructions for this problem are similar to those of 8.2 last time.

      You should probably make larger copies of these figures with graph paper. Mark the mirror lines of the reflection symmetries and glide reflection lines of the glide reflection symmetries, and then indicate a lattice defined by the translation symmetries.

      Do this for the following figures in Bix, 8.1: a), c), e), g), h).

    3. Symmetry groups of certain figures (20 points)

In each case, tell what isometries are symmetries of the figure. Also tell how you ruled out all the others.

  1. A figure made of a line m and a point A not on the line.
  2. A figure consisting of a line m and a point A on the line.
  3. A figure consisting of a line segment AB.
  4. A figure made of two lines m and n intersecting at a point A. (Include all cases.)
    1. Composition and Conjugation (20 points)
  1. Let H be the halfturn (rotation by 180 degrees) with center A and let M be the reflection in line m. The point A is not on m; the distance from A to m is d. Prove that F = MH is a glide reflection G determined by two points P and Q. Tell what P and Q will make this correct and prove that F = G.
  2. Prove that MHM is a halfturn. Tell what the center is and prove that this isometry is a halfturn.
  3. Prove HMH is a line reflection. Tell what the mirror is and prove that this isometry is a line reflection.

Email Discussion for Extra Credit

Analyze the symmetries of m),n), o) or u) for extra credit. Same instructions as before.