Note: Problem 6.1 is revised from the version handed out in class Monday, 10/19.

Assignment 6 (65 points, Due Monday 10/26)

Problem 6.1 (5 points)

Let m be a line and let d be a positive number. Let N be the set of points P for which the distance from P to the line m is d. Prove that N consists of two lines, n1 and n2, each of which is parallel to m.

Problem 6.2 (15 points)

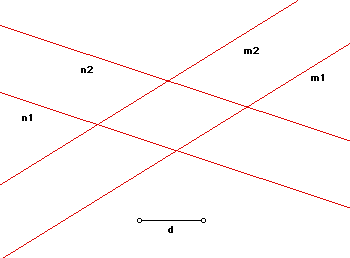
Suppose you draw two parallel lines m1 and m2 with a ruler by placing the ruler on a sheet of paper and running a pencil up and down both edges of the ruler without moving the ruler. Then move the ruler, rotating a bit so that the edges are no longer parallel to the lines m1 and m2. Now as before draw another pair of parallel lines n1 and n2 by tracing both edges of the ruler.

You have drawn a figure like the one below, consisting of two parallel lines, each pair being the same distance d apart. Prove that the quadrilateral ABCD defined by the four points of intersection of the lines is a rhombus.

Given two lines m and n intersecting at A, these lines define four angles with vertex at A. Prove that a point P is equidistant from m and n if and only if the ray AP is the bisector of one of these four angles.

 

Problem 6.3 (30 points)

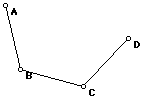
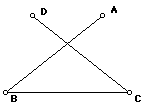
In both figures below, angle ABC = angle BCD and all 3 segments have equal length: |AB| = |BC| = |CD|. In each case (a-f) tell whether your answer applies to both figures or whether what is true (or the proofs or constructions) for the second figure is different.

  1. Prove that there is a circle which passes through ABCD. (Hint: What do you need to prove as a first step; think of circumcircles for triangles.)
  2. Construct an example of a figure like ABCD and also construct the circle through ABCD.
  3. Prove that there is a circle which is tangent to the segments AB, BC, and CD.
  4. Construct an example of a figure like ABCD and also construct the circle tangent to the 3 segments (whose existence was proved in (c.)).
  5. Tell how the centers of the two circles are related (and prove it).
  6. Tell what are the lines of symmetry of this figure (and prove it).

 

Problem 6.4 (15 points)

B&B, page 116, #25, 26

 Back to Math 444 Home Page